Инвестиции - Колтынюк Б.А.. Удк 336 ббк 65. 26 К 61

• Название: Удк 336 ббк 65. 26 К 61
• Анкор: Инвестиции - Колтынюк Б.А..doc
• Дата: 18.12.2017
• Размер: 24.66 Mb.
• Имя файла: Инвестиции - Колтынюк Б.А..doc
• Тип: Книга; #12033
• Категория: Экономика. Финансы
• страница: 45 из 72

19.2. Оценка ренты

Одним из важнейших показателей, используемых при оценке и анализе инвестиционных проектов, ценных бумаг и характеризующих потоки денежных средств, являются потоки денежных средств или рента (аннуитет). Первоначально рассматривались лишь ежегодные (anno — год на латинском языке) потоки, откуда и произошло их название «аннуитент». Позднее оно стало включать и все последовательности потоков одного знака через любые одинаковые интервалы времени. К числу таких потоков относя вложения в банк на срочный депозит с целью получения ежегодного дохода, предоставление кредита под банковский процент и др.

Под, рентой инвестиционного проекта понимают такой поток постоянных годовых доходов, настоящая стоимость которого в течение всего периода использования объекта совпадает с его чистой настоящей стоимостью. В практике под аннуитетом инвестиционного проекта чаще всего понимают поток постоянного годового дохода, который может извлечь инвестор при реализации проекта.

Используя формулу 19.17, можно получить настоящую стоимость ренты пренумерандо, подлежащей к выплате с будущего периода: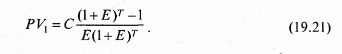


Настоящая стоимость ренты пренумерандо представляет собой произведение рентного платежа на специальный коэффициент, называемый коэффициентом настоящей стоимости ренты пренумерандо, или коэффициентом наращения ренты (аннуитета), выплачиваемой с будущего периода. Наращенная или будущая стоимость денежной суммы означает проекцию заданной в настоящий момент суммы вперед, в будущее. Приведение суммы к определенному моменту времени состоит в ее умножении на множитель приведения, который равен множителю наращивания.

С помощью коэффициента наращивания можно привести будущие постоянные ежегодные платежи в течение Т лет в эквивалентный платеж настоящего периода. Если С — сумма, которую инвестор собирается получать в течение Т лет, Е — ставка процента или доходности, то PV₁ представляет собой денежный эквивалент этого потока доходов при данной ставке процента. Помещая эту сумму в банк под указанный процент, инвестор обеспечивает тем самым желаемый поток постоянных доходов в течение периода Т.

Аналогично можно получить коэффициент будущей стоимости финансовой ренты (табл. 19.2).

Таблица 19.2

Коэффициенты настоящей и будущей стоимости рент пренумерандо

Необходимо заметить, что при одинаковых периодах потоков денег коэффициенты настоящей и будущей стоимости ренты постнумерандо, выплачиваемой с настоящего периода, совпадает с соответствующими коэффициентами ренты пренумерандо, выплачиваемой с будущего периода.

Пример. Инвестор в начале года кладет определенную сумму денег на банковский счет, по которому банк обещает выплачивать из расчета 80% годовых. Он рассчитывает ежегодно в течение 10 лет, начиная со следующего года получать 5 млн руб. Надо определить необходимую сумму вклада.

Поскольку инвестор собирается ежегодно снимать со счета деньги равными суммами в начале года, то речь идет о ренте пренумерандо, выплачиваемой с будущего года. Для определения суммы вклада необходимо найти настоящую стоимость данного вклада с ежегодным платежом С = 5 млн руб., периодом Т = 10 лет и ставкой доходности Е = 80%. Тогда в соответствии с формулой, представленной в таблице 19.2, получим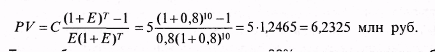


Таким образом, при ставке доходности 80% годовых и вкладе в банк 6,2325 млн руб. можно снимать в течение 10 лет ежегодно 5 млн руб. Если ставка доходности повышается, к примеру до 180%, то сумма вклада составит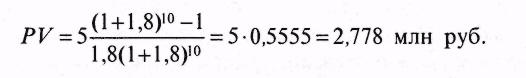


Расчеты также показывают, что если ставка банковского процента меньше 100%, то настоящая стоимость ренты (сумма вклада), выплачиваемой с будущего периода банком, больше рентного платежа. Если же она больше 100%, то, наоборот, настоящая сумма вклада меньше рентного платежа.

Определим будущую стоимость той же ренты с ежегодным платежом 5 млн руб. при тех же условиях банка. Такая задача каждый раз возникает в тех случаях, когда надо определить будущую стоимость ренты пренумерандо. Используя формулы, приведенные в таблице 19.2, получим

Из приведенного расчета видно, что если в начале каждого года вносить в банк 5 млн руб., то за период времени Т = 10 лет при Е = 80% на счете инвестора окажется 2225,292 млн руб.

Если же ставку банковского процента увеличить, к примеру в 2,25 раза, т.е. до Е = 180%, то будущая стоимость ренты увеличится в 37 раз и составит


Рассмотрим пример расчета ренты пренумерандо, выплачиваемой с настоящего периода.

Пример. Инвестор вносит в банк в начале каждого года в течение 12 лет 0,5 млн руб. Надо определить, какая сумма средств окажется на его счете, если ставка банковского процента составляет 180% годовых. Для расчета используем формулу, приведенную в табл. 19.2.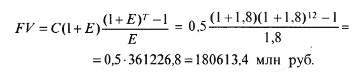

Существуют и другие возможности оценки инвестиций эффективности на основе ренты пренумерандо.

В зависимости от срока, объема денежных поступлений и начисляемых при этом процентов аннуитеты могут быть:

• 
  срочные;
  
• 
  с изменяющейся величиной платежа;
  
• 
  бессрочные.
  

Если число равных временных интервалов ограничено, аннуитет (А) называется срочным. В этом случае:

Примером срочного аннуитета могут служить регулярно поступающие рентные платежи за пользование сданным в аренду земельным участком в случае, если договором предусматривается регулярная оплата аренды по истечении очередного периода. В качестве срочного пренумерандо может выступать, к примеру, схема периодических денежных вкладов на банковский счет в начале каждого месяца с целью накопления достаточной суммы для крупной покупки. Наращенный денежный поток для исходного положения потока постнумерандо имеет вид:


Прямая задача оценки срочного аннуитета при заданных величинах регулярного поступления (А) и процентной ставки (Е) предполагает оценку будущей стоимости аннуитета. При этом наращенный денежный поток имеет вид: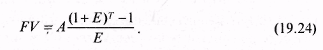

Входящий в формулу множитель [(1 + Е)^Т - 1]/Е называется коэффициентом наращения ренты для аннуитета, или коэффициентом наращения аннуитета. Он представляет собой сумму п первых членов геометрической прогрессии, начинающейся с 1 и знаменателем (1 + Е).

Из формулы (19.24) следует, что [(1 + Е)^Т - 1]/Е показывает, во сколько раз наращенная сумма аннуитета больше величины денежного поступления А. В связи с этим множитель называют коэффициентом аккумуляции вкладов.

Отметим, что формула (19.24) охватывает также и граничные случаи. Например, при одном денежном поступлении (Т = 1):

а при Е = 0 не происходит никаких начислений, т.е. денежные поступления просто суммируются.

Экономический смысл коэффициента наращения ренты состоит в том, что он показывает: чему будет равна суммарная величина срочного аннуитета в одну денежную величину (например, один рубль) к концу срока его действия. При этом предполагается, что производится только начисление денежных сумм, а их изъятие может быть сделано по окончании срока действия аннуитета. Коэффициент наращения ренты весьма часто используется в финансовых расчетах. Его значение зависит от процентной ставки (Е) и срока (п) действия аннуитета. Причем при увеличении каждого из этих параметров величина множителя также прирастает.

Пример. Вам предлагают сдать в аренду здание на три года, выбрав один из двух вариантов оплаты аренды:

а) 100 тыс. руб. в конце каждого года;

б) 350 тыс. в конце трехлетнего периода.

Какой вариант будет более предпочтителен, если банк предлагает 20% годовых по вкладам?

Первый как раз и представляет собой аннуитет постнумерандо при Т = 3 и А = 100 тыс. руб. В этом случае имеется возможность ежегодного получения арендного платежа и инвестирования полученных сумм как минимум на условиях 20% годовых (например, вложение в банк). К концу трехлетнего периода по расчетам по формуле 19.24 накопленная сумма составит:


Таким образом, расчет показывает, что первый вариант более предпочтителен, чем второй, поскольку 364 тыс. руб. > 350 тыс. руб.

Обратная задача оценки срочного аннуитета постнумерандо сводится к определению будущих поступлений с позиций текущего момента, под которым в данном случае понимается момент времени, начиная с которого определяются равные временные интервалы, входящие в аннуитет. Схема дисконтирования денежных потоков приведена ранее (см. рис. 19.1).

Используя данные указанного примера, получим сумму денежного потока постнумерандо в начальном периоде (текущую стоимость):


Коэффициент дисконтирования ренты (аннуитета) или коэффициент наращения ренты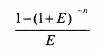

показывает, чему равна с позиции текущего момента величина аннуитета с регулярными денежными поступлениями в размере одной денежной единицы (например, один рубль), продолжающегося п равных периодов с заданной процентной ставкой Е.

Так, для указанного примера при Е = 20% PV = 211,11 тыс. руб. При одном денежном поступлении и Е = 0, PV = FV.

Дисконтирующий множитель представляет определенный практический интерес при помещении капитала под сложный процентную ставку Е в банк. Тем самым можно обеспечить регулярные выплаты в размере одной денежной единицы в течение п периодов. При этом выплаты производятся в конце каждого периода. Тогда будущая стоимость аннуитета пренумерандо может быть найдена по формуле:

Аналогично полученному значению может быть найдена приведенная стоимость аннуитета пренумерандо:

Рассмотрим следующий пример.

Пример. Предположим, что Вам предложено инвестировать 100 тыс. руб. на срок 5 лет при условии возврата ежегодно этой суммы частями по 20 тыс. руб. По истечении пяти лет выплачивается ежегодное вознаграждение в размере 30 тыс. руб. Надо ли принимать это предложение, если можно положить их в банк под 12% годовых?

Для принятия решения необходимо сравнить поступления денег между собой от этих вариантов.

От альтернативного варианта помещения денег на срочный депозит в конце пятилетнего периода получим

FV = 100 (1 + 0,12)⁵ = 176,23 тыс. руб.

Денежный поток при этом можно представить двояко:

а) как срочный аннуитет постнумерандо с А = 20, п = 5, Е = 20% и единовременное получение суммы в размере 30 тыс. руб.;

б) срочный аннуитет пренумерандо с А = 20, п = 4, Е = 20% и единовременное получение сумм в размере 20 и 30 тыс. руб.

Тогда по формуле (19.25) в первом случае получим 157,06 тыс. руб.

Во втором случае по формуле (19.26) получим 157,06 тыс. руб.

Оба эти варианта привели к одинаковому результату.

Следовательно, предложение экономически невыгодно.

В ряде случаев при формировании денежных средств для реализации инвестиционного проекта определенный интерес представляет метод депозитной книжки. Суть ее заключается в том, что сумма, положенная на депозит, приносит доход в виде банковских процентов. При снятии с депозита некоторой суммы базовая величина, с которой начисляются проценты, уменьшается. Чаще всего такая ситуация и имеет место в случае с аннуитетом. Следовательно, под текущей стоимостью аннуитета можно понимать величину депозита с общей суммой причитающихся начисляемых процентов, которая ежегодно уменьшается па равные суммы. При этом сумма годового платежа включает в себя начисленные за очередной период проценты, а также некоторую часть основной суммы долга. В результате погашение исходного долга осуществляется в течение всего срока аннуитета. Соответственно структура годового платежа постоянно меняется по мере сокращения долга и суммы от начисленных процентов.

Рассмотрим следующий пример.

Пример. Инвестор для расчетов с исполнителями инвестиционного проекта положил на депозитный счет 30 тыс. руб. на пять лет под 13%, начисляемых по схеме сложных процентов на непогашенный остаток. Рассчитываться с исполнителями проекта надо равными суммами в конце каждого года.

Если обозначить за А величину искомого платежа, то данные соглашение с банком можно представить в виде следующей схемы (рис. 19.3)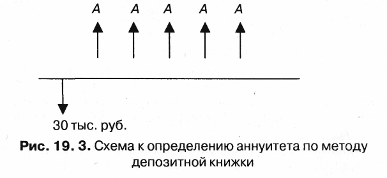


С позиций инвестора указанная схема на рис. 19.3 представляет собой последовательность расчета с исполнителями проекта. Для этого инвестор открывает депозитный счет в банке, который выступает заемщиком, берущим под 13% годовых заем. Таким образом инвестор предполагает осуществлять равные по годам выплаты.

Поскольку в течение первого года банк пользуется полной суммой вклада инвестора, то, соответственно, сумма платежа (оттока денежных средств) исполнителям будет состоять из начисленных процентов, равных 3,9 [30 (1 + 1,13)], и оставшейся части, составляющей: А - 3,9. В последующих периодах времени аналогичный расчет будет повторяется при условии, что сумма первоначального вклада инвестора будет сокращаться, а доля платежа возрастать. Например, после окончания второго года банк также перечислит исполнителям определенную инвестором сумму. При этом размер денег от начисляемых банком процентов будет сокращаться по мере его расчетов с исполнителями.

Для определения годового платежа А используем формулу 19.26.

Тогда


где А = 30 /3,517 = 8,53 тыс. руб.

На практике возможны ситуации, когда денежные поступления продолжаются достаточно длительное время. В этих случаях аннуитет называется бессрочным, или вечной рентой, т.е. п → ∞. К бессрочным аннуитетам в зарубежной практике относят аннуитеты, рассчитанные на 50 и более лет. Поскольку определение будущей стоимости поступлений не имеет смысла, нахождение приведенной стоимости представляет определенный практический интерес.

Для бессрочного аннуитета постнумерандо используется следующая формула


Формула (19.27) показывает, что поток даже с неограниченным числом платежей имеет все же конечную приведенную к начальному моменту времени стоимость.

Таким образом, рассмотренные денежные потоки в виде рент и аннуитетов с финансовой точки зрения представляют практический интерес при выборе рациональной схемы финансирования.