расчет. Удк 621. 919 Р

• Название: Удк 621. 919 Р
• Анкор: расчет
• Дата: 26.04.2023
• Размер: 1.09 Mb.
• Имя файла: raschet-diskovoy-modulnoy-frezy-dlya-narezaniya-kosozubogo-koles.docx
• Тип: Документы; #1090872
• страница: 5 из 10

Напервомэтапебыло выполнено моделирование тела исходной инструментальной по-верхности (ИИП) полученной выше дисковой модульной фрезы.


^R

R

i
i1⁼i^{Rдля Rвн  R Rнар(z}i<sup>);

</sup>_i1=_i для0_i360; (1) ^zi1^=zi^{zдля-L/2 z}i^{ L/2,}

где R_i, _i, z_i– координаты i-го вокселя в цилиндрической системе координат фрезы;

R, , z– приращения шага воксельной сетки по трем координатам;

R_вн , R^н_ар(z_i), L– внутренний (посадочного отверстия), наружный (по профилю, завися-щему от z) диаметры фрезы и ее толщина.

Полученное при решении прямой задачи множество точек профиля ИИП дисковой фрезы

может быть с достаточной для практики точностью аппроксимировано сплайновой линией. Од-нако при большом числе точек и достаточно малом расстоянии между ними этот профиль может быть также достаточно точно аппроксимирован дугами окружностей, проведенными по трем точкам, указанного множества. В частности, такие программы, как Solidworks позволяют постро-ить требуемые дуги окружностей и сразу же получить все их параметры: их радиус r, координа-ты центра (A,B), координаты начальной и конечной точек (x,z). В этом случае искомый радиус-вектор точек профиля фрезы можно определить как


2
^Rнар(z_i^{)  r}_j^_^z_i^{ A}_j2 ^B_j^{для z}i1^=zi^{zдля z}sj^{ z}i^{ z}ej^{, (2)} где r_j, A_j, B_j– радиус текущей j-й дуги окружности профиля ИИП дисковой фрезы и коор-

динаты ее центра в системе координат фрезы;

_{zsj, zej}– аппликаты стартовой и конечной точек дуг окружностей, аппроксимирующих про-

филь ИИП фрезы.

Навторомэтапепо общеизвестным формулам перехода от цилиндрической системы коор-динат в декартову такие координаты ( x_i,y_i,z_i) точек вокселей фрезы пересчитываются для сис-темы координат заготовки зубчатого колеса ( _xfi,yfi,zfi):

56

Bulletin of the South Ural State University. Ser. Mechanical Engineering Industry. 2022, vol. 22, no. 4, pp. 52–62

ЩуровИ.А. Расчетдисковоймодульнойфрезыдлянарезаниякосозубогоколеса…


^ 

 
^x_fi ^A_n^{ } ₁ ^{ x}_i^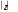

_ ^y_fi ^{ M}_x^(_n^)M_y^(_n^)M_z^(_n⁾_^B_n^...M_x^(₁^)M_y^(₁^)M_z^(₁⁾_^B_^_^y_i , (3)  ^fi ^{n 1 i}

где M_k(_i) – матрицы преобразований поворота систем координат вокруг осей k = (x, y, z) на углы _i= (_i, _i, _i);

_i, _i, _i– угловые параметры начальной установки инструмента относительно заготовки зубчатого колеса и параметры его формообразующего движения;

A_i, B_i, C_i– величины переноса координат по трем осям, аналогично угловым параметрам – параметры начальной установки и движения инструмента;

_Применительно к данной задаче необходимо выполнить последовательно следующие преоб-разования систем координат. Во-первых, необходимо перенести точки вокселей фрезы на рас-стояние ее радиуса в направлении, обратном к оси ординат (B₁). Во-вторых, необходимо повер-_{нуть такие точки на угол 180° (}M_z(₁)_{), что связано с фактом обращения зубьев фрезы к оси за-}готовки зубчатого колеса. В-третьих, необходимо снова перенести точки фрезы вдоль оси ординат на расстояние, равное радиусу окружности впадин зубчатого колеса (B₂). В-четвертых, необходимо повернуть точки фрезы на угол установки фрезы для обработки винтовой канавки _{косозубого колеса (}M_y(₁)_{). При необходимости можно сместить точки фрезы вдоль ее оси, то}

есть использовать третий параметр ее установки. В нашем случае, как видно из третьей строки формулы (1), фреза моделировалась симметрично оси ординат, так же, как выполнялось модели-рование при решении прямой задачи.

Далее необходимо выполнить моделирование движения формообразования фрезой. В про-цессе фрезерования косозубого колеса, например, на горизонтально-фрезерном станке с исполь-зованием делительной головки и ее вращения от гитары шестерен с приводом их от винта подачи стола станка, фреза перемещается вдоль оси ординат с одновременным вращением вокруг нее. Такие перемещение и вращение дают винтовое движение фрезы относительно заготовки зубчато-го колеса. Очевидно, что угол наклона касательной к винтовой линии такого движения должен быть равен углу наклона зуба зубчатого колеса. При этом цилиндр, на котором расположена дан-ная винтовая линия, должен касаться цилиндра зубчатого колеса, на котором выполняется опре-деление соответствующего угла для винтовой линии зуба колеса. Расчет шага винтовой линии и связанного с ним винтового параметра винтовой линии выполняется по общеизвестным форму-лам, включающим в себя указанный выше угол и диаметр цилиндра с расположенной на нем винтовой линией. Также очевидной является и взаимосвязь величины дискреты перемещения фрезы p(₂ )  p₂ с ее поворотом относительно оси колеса ₂ , где p– отмеченный выше винтовой параметр. Остальные параметры универсальной зависимости (3) принимаются равными нулю.


   
Натретьемэтаперасчетов необходимо определить профиль впадины зубчатого колеса, который будет сформирован ранее рассчитанной фрезой. Очевидно, что нет необходимости вы-полнять операцию разности множеств цилиндрической заготовки зубчатого колеса и полученно-го множества точек вокселей множеств фрезы при ее формообразующем движении. Достаточно выбрать точки сечения последнего множества в требуемом сечении. Таким сечением может быть сечение в плоскости параллельной торцовой плоскости цилиндра зубчатого колеса. Эта плос-кость оказывается удобной, поскольку в ней хорошо отражается профиль впадины колеса в его исходной CAD-модели. Для выбора указанных точек из общего их множества достаточно уста-новить интервал выборки: y_e y_i y_e1, где y_e(min y_imax y_i)/2.

Результатыдискретноготвердотельногомоделирования. Приведенные выше формулы позволили получить множество точек фрагмента дисковой фрезы (рис. 5, а, б, в).

Множество точек фрагмента внутри ИИП фрезы при ее винтовом движении с заданной дис-кретой образует семейство таких фрагментов и их точек (рис. 5, г). Выбранные двумя секущими