Математика. Укажите область определения функции Какая поверхность называется графиком функции n переменных
 Скачать 434.78 Kb. Скачать 434.78 Kb.
|
|
прямые перпендикулярны 6) Укажите канонические уравнения прямой 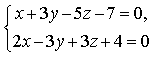 7) Найдите острый угол между прямыми 60° 8) Составьте уравнение плоскости, проходящей через параллельные прямые 6x— 20y— 11z+ 1 = 0 9) Даны вершины треугольника ABC: A(3; -1),B(4; 2) и C(-2; 0). Напишите уравнения его сторон 3x—y— 10 = 0, x— 3y+ 2 = 0, x+ 5y+ 2 = 0 10) Уравнение 3x— 4y+ 12 = 0 преобразуйте к уравнению в отрезках 11) Определите уравнение прямой, отсекающей на оси Oy отрезок b = 2 и составляющей с осью Ox угол j= 45° y=x+ 2 12) Найдите координаты точки пересечения прямых 2x—y— 3 = 0 и 4x+ 3y— 11 = 0 (2; 1) 13) Найдите уравнение прямой, проходящей через точки M1(3; 2), M2(4;-1) 3x+y— 11 = 0 Ответы на модуль 4 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика. 1) Определите эксцентриситет равносторонней гиперболы 2) Укажите уравнение окружности, которая проходит через точки А(3;1) и В(-1; 3), а ее центр лежит на прямой 3x—y— 2 = 0 (x— 2)2+ (y— 4)2= 10 3) Укажите уравнение окружности радиуса R= 8 с центром в точке C(2;-5) (x— 2)2+ (y+ 5)2= 82 4) Определите полуоси гиперболы a= 4, b= 1 5) Укажите уравнение окружности, центр которой совпадает с началом координат, а прямая 3x— 4y+ 20 = 0 является касательной к окружности x2+y2= 16 6) Укажите уравнение окружности, которая проходит через точку А(2;6) и ее центр совпадает с точкой C(-1; 2) (x+ 1)2+ (y— 2)2= 25 7) Укажите каноническое уравнение эллипса, расстояние между фокусами которого равно 8, а малая полуось b= 3 8) Напишите уравнение эллипса, если даны его полуоси a= 5 и b= 4 9) Укажите уравнение окружности, проходящей через точку (4; 5) с центром в точке (1; -3) (x— 1)2+ (y+ 3)2= 73 10) Определите полуоси гиперболы 25x2— 16y2=1 11) Напишите уравнение гиперболы, фокусы которой лежат на оси Ox, если даны a= 6 и b= 2 12) Укажите уравнение параболы, с вершиной в точке O и фокусом F(4; 0) y2=16x 13) Укажите уравнение окружности, для которой точки А(3; 2) и В(-1; 6) являются концами одного из диаметров (x— 1)2+ (y— 4)2= 8 Ответы на модуль 5 (КРИВАЯ 2-ГО ПОРЯДКА) по предмету математика. 1) Найдите общее решение системы 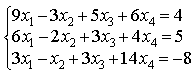 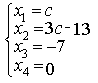 или или 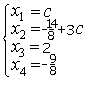 2) Вычислите определитель 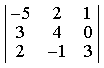 -89 3) Найдите ранг и базисные строки матрицы 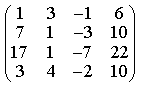 2. 1-я строка, 2-я строка 4) Вычислите определитель 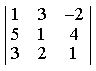 0 5) Найдите А × В, где 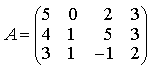 ; ; 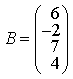 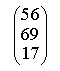 6) Решите систему уравнений методом Крамера 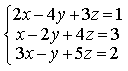 {(-1; 0; 1)} 7) Найдите обратную матрицу для матрицы 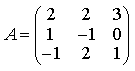 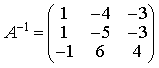 8) Найдите ранг матрицы 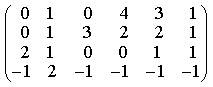 4 9) Определитель системы трех линейных уравнений с тремя неизвестными равен 5. Это означает, что система имеет единственное решений 10) Найдите АВ — АС, где ; ; 11) Метод Гаусса решения системы линейных уравнений предполагает использование последовательного исключения неизвестных 12) Система линейных уравнений называется совместной, если она имеет хотя бы одно решение 13) Решите матричное уравнение AX + AXA = B, где Ответы на модуль 6 (МАТЕМАТИЧЕСКИЙ АНАЛИЗ) по предмету математика. 1) Найдите предел 3 2) Найдите предел 5 3) Найдите предел 5 4) Найдите предел 1/e 5) Найдите предел 0 6) Найдите предел 0 7) Найдите предел 8) Найдите предел 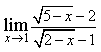 1/2 9) Найдите предел 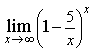 e—5 10) Найдите предел 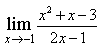 1 11) Найдите предел 0 12) Найдите предел 5/3 13) Найдите предел 3/5 Ответы на модуль 7 (ДИФФЕРЕНЦИРОВАНИЕ) по предмету математика. 1) Вычислите предел по правилу Лопиталя 0 2) Найдите производную функции f(x)=(1+ cos x)sin x cos x+ cos 2x 3) Вычислите предел по правилу Лопиталя 1/18 4) Вычислите предел по правилу Лопиталя -4/3 5) Найдите производную функции y= sin(2x2+ 3) 4xcos(2x2+ 3) 6) Найдите производную функции y=(3ex+x)× cos x (3ex+ 1) × cos x— (3ex+x) × sin x 7) Для функции найдите y(49) 1/14 8) Найдите производную функции 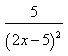 9) Найдите производную функции y=2tgx 10) Найдите производную функции 11) Найдите скорость тела, движущего по закону S=3t-5 3 12) Дана функция 13) Найдите производную функции y=xex—ex xex Ответы на модуль 8 (ИССЛЕДОВАНИЕ ФУНКЦИИ С ПОМОЩЬЮ ПРОИЗВОДНОЙ) по предмету математика. 1) Число f(x0) называется наибольшим значением функции на отрезке [a;b], если для всех x из этого отрезка выполняется неравенство f(x) <= f(x0) 2) Найдите промежутки возрастания или убывания функции y=x2— 3x+ 1 убывает при x<3/2, возрастает при x>3/2 3) Найдите точки максимума (минимума) функции y=- 5x2— 2x+ 2 (-0,2;2,2) — точка максимума 4) Каково необходимое условие возрастания функции? если функция y=f(x) дифференцируема и возрастает на интервале (a;b), то f(x)>=0 для всех xиз этого интервала 5) Определите поведение функции y= 2x2 при x= 1 возрастает 6) В каких точках выпукла или вогнута кривая y=x2— 3x+ 6 вогнута во всех точках 7) Найдите промежутки возрастания или убывания функции y=- 2x2+ 8x— 1 убывает при x> 2, возрастает x< 2 8) Найдите точку перегиба кривой (0; 0) 9) Найдите точки перегиба кривой y=x4— 12x3+ 48x2— 50 (2; 62) и (4; 206) 10) Найдите точки максимума (минимума) функции y=x2— 2x (1;-1) — точка минимума 11) Вертикальные асимптоты к графику функции x= 4, x= 0 12) Найдите наибольшее и наименьшее значения функции y=x2 на промежутке [-1; 3] yнаиб= 9, yнаим= 0 13) В каких точках выпукла или вогнута кривая y= 2 — 3x—x2 выпукла во всех точках Ответы на модуль 9 (ФУНКЦИЯ НЕСКОЛЬКИХ ПЕРЕМЕННЫХ) по предмету математика. 1) Найдите частные производные функции двух переменных 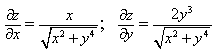 2) Найдите частные производные второго порядка функции z=x3y4+ycos x 3) Найдите предел функции 0 4) На каком из рисунков изображена область определения функции 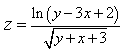 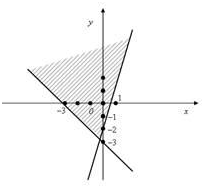 5) Найдите частные производные функции двух переменных z=xey+yex 6) Найдите частные производные функции z=x2× ln y  7) Найдите полный дифференциал функции z=x2y+xy2 dz=(2xy+y2)dx+(x2+2xy)dy 8) Какая поверхность называется графиком функции n переменных? n-мерная гиперповерхность в пространстве Rn+ 1, точки которой имеют вид (х1, х2, …, хn, f(x1, х2, …, xn)) 9) Укажите полное приращение функции f(x;y) f(x +Dx; y +Dy)- f(x; y) D-треугольничек. 10) Найдите  |
