Дополнительные свойства параллелограмма. свойства параллелограмма. Урок Дополнительные свойства параллелограмма
 Скачать 109.2 Kb. Скачать 109.2 Kb.
|
|
Открытый урок «Дополнительные свойства параллелограмма» Цель урока: Систематизировать, обобщить знания о параллелограмме, рассмотреть и доказать дополнительные свойства параллелограмма. Задачи: - предметные: умение проводить логические обоснования, доказательства математических утверждений; формирование умения построения математической модели решения задач. - метапредметные: умение выдвигать гипотезы при решении учебных задач, понимать необходимость их проверки; развивать логическое мышление, познавательную активность и навыки научной речи. - личностные: создание педагогических условий для формирования у обучающихся положительной мотивации к учению, умения преодолевать посильные трудности, чувства коллективизма, взаимовыручки и уважения друг к другу, умения вести диалог, понимать смысл поставленной задачи; выстраивать аргументацию, приводить примеры. Тип урока: открытие новых знаний. Основные методы обучения:наглядный,репродуктивный, практический и исследовательский. Формы организации учебной деятельности: фронтальная, индивидуальная, самостоятельная, групповая. Девиз урока: «Математику уже затем учить надо, что она ум в порядок приводит.» (М. В. Ломоносов). Ход урока. 1.Организационныйт этап. Хоть стороны мои Попарно и равны, и параллельны, Все ж я в печали, что не равны мои диагонали, Да и углы они не делят пополам Но все ж, скажи, дружок, кто я? (Параллелограмм) Историческая справка (Полина) Термин «параллелограмм» греческого происхождения и, согласно древнегреческому философу Проклу, был введен Евклидом. Евкли́д — древнегреческий математик, автор первого из дошедших до нас теоретических трактатов по математике. Биографические сведения об Евклиде крайне скудны. Достоверным можно считать лишь то, что его научная деятельность протекала в Александрии в III в. до н. э. Понятие параллелограмма и некоторые его свойства были известны еще пифагорейцам. Пифагореи́зм — религиозно-философское учение, возникшее в Древней Греции VI—IV вв. до н. э. (также известно как пифагорейство). Получило название по имени своего родоначальника Пифагора. Полная теория параллелограммов была разработана к концу средних веков и появились в учебниках лишь в XVII веке. Все теоремы о параллелограммах основываются непосредственно или косвенно на теореме Евклида о свойствах параллелограмма. Само же понятие параллелограмм от греч. Parallelos — параллельный и gramme — линия. Поэтому слово «параллелограмм» можно перевести как «параллельные линии». 2. Актуализация знаний обучающихся Можно сказать, что параллелограмм - одна из значимых фигур в планиметрии. Он обладает интересными свойствами и достоинствами. А вот какими, вы сейчас вспомните. (один ученик у доски, спрашивает учащихся и показывает элементы на чертеже, соответствующие ответу) (Стас) В это время двое учащихся отвечают тест за компьютерами (Саша, Толик) Тест (варианта):
Самопроверка 3. Изучение новых свойств А сейчас я предлагаю вам подумать верные или нет данные утверждения и объяснить, почему вы так считаете: Работа в группах: обсудили утверждения, отвечаем по очереди. 1. Любой четырехугольник является параллелограммом. (объясняют) 2. У параллелограмма могут быть все углы равны. (объясняют) 3. У параллелограмма две стороны параллельны, две другие нет. (объясняют) 4. У параллелограмма биссектриса угла отсекает равнобедренный треугольник. (вызывает затруднение, доказываем вместе) (Кирилл П) Вывод: 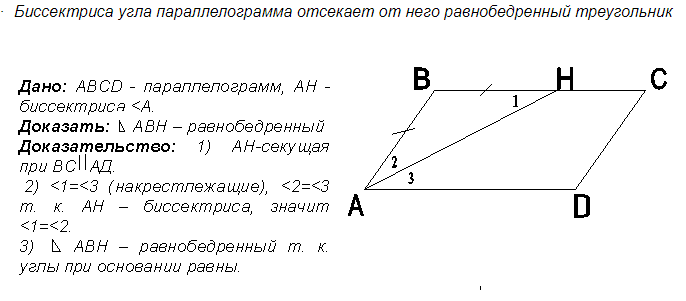 Физкультминутка: Если утверждение верное, поднимаете руки, вытягиваете спину и опускаете руки вниз, если ложное – встаете со стула, поднимаетесь на носочки и садитесь, если я называю утверждение, в котором вы сомневаетесь – зажмурились, закрыли глаза руками, открыли глаза. Прямоугольник – это параллелограмм. (руки вверх…) У параллелограмма все углы острые. (встаем…) Любой параллелограмм является четырехугольником. (руки вверх…) Периметр параллелограмма – сумма двух его сторон. (встаем…) Середины сторон параллелограмма являются вершинами нового параллелограмма. (качаем головой…, доказываем вместе) (Даша) Вывод: 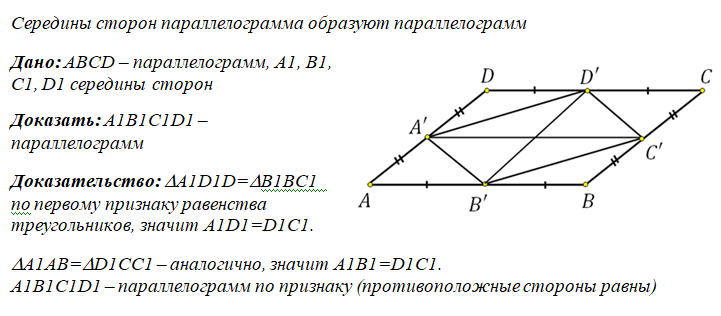 Практическая работа: постройте параллелограмм. С помощью циркуля и линейки постройте биссектрисы углов параллелограмма. Какая фигура образовалась при пересечении биссектрис. Проверьте данное утверждение с помощью угольника или транспортира. (Максим) Внимание! Используем циркуль только по назначению, если необходимо передать циркуль товарищу, передайте держателем вперед, не играйте инструментом, не пытайтесь уколоть себя или товарища. Вывод: Биссектрисы углов параллелограмма при пересечении образуют прямоугольник А докажем мы это свойство позже, когда изучим свойства прямоугольника и поговорим о его признаках. Домашнее задание: доказать следующие дополнительные свойства параллелограмма: Диагональ делит параллелограмм на два равных треугольника. Биссектрисы углов прилежащих одной стороне при пересечении образуют прямой угол. 4.Рефлексия: игра «Танграм» Составить прямоугольник, параллелограмм, равнобедренный треугольник, трапецию 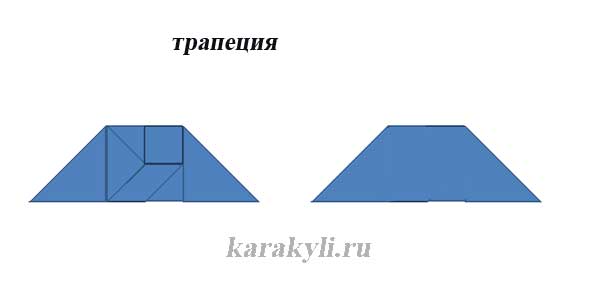 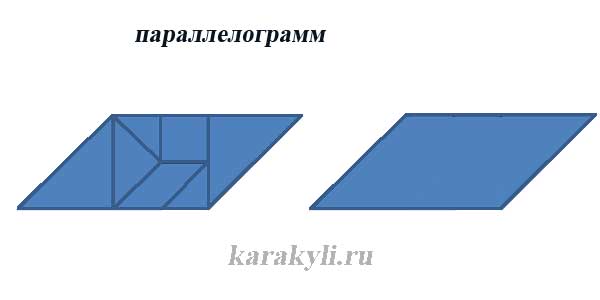   Какие новые свойства параллелограмма мы сегодня изучили? Для чего они нам пригодятся? Нужны ли нам свойства параллелограмма в повседневной жизни? (РАЗРАБОТАНЫ ПОГРУЗЧИКИ И ПОДЪЕМНИКИ, АВТОМОБИЛЬНЫЕ ДВОРНИКИ, ШТАТИВЫ, АВТОМОБИЛЬНЫЕ ПОДВЕСКИ, РАЗДВИЖНЫЕ РЕШЕТКИ, ТОКОПРИЕМНИК У ТРАМВАЯ) Понравился ли Вам урок? Ресурсы: http://www.karakyli.ru/2014/07/23/tangram-igra-dlya-detej http://repetitor-problem.net/dopolnitelnyie-svoystva-i-priznaki-parallelogramma https://pandia.ru/text/78/199/9825.php https://ru.wikipedia.org |
