Статистика. Курс лекций Статистика. Урок Введение. Предмет, метод, задачи статистики План
 Скачать 469.82 Kb. Скачать 469.82 Kb.
|
Раздел 5.
Рассчитанные в последней графе данной таблицы проценты представляют собой относительные показатели структуры (в данном случае - удельные веса). Сумма всех удельных весов всегда должна быть строго равна 100% или 1. Относительный показатель координации представляет собой отношение одной части совокупности к другой части этой же совокупности:  При этом в качестве базы сравнения выбирается та часть, которая имеет наибольший удельный вес или является приоритетной с экономической, социальной или какой-либо другой точки зрения. В результате получают, во сколько раз данная часть больше базисной или сколько процентов от нее составляет, или сколько единиц данной структурной части приходится на 1 единицу (иногда - на 100, 1000 и т.д. единиц) базисной структурной части. Относительный показатель интенсивности характеризует степень распространения изучаемого процесса или явления и представляет собой отношение исследуемого показателя к размеру присущей ему среды:  Данный показатель получают сопоставлением уровней двух взаимосвязанных в своем развитии явлений. Поэтому, наиболее часто он представляет собой именованную величину, но может быть выражен и в процентах, промилле, продецимилле. Обычно относительный показатель интенсивности рассчитывается в тех случаях, когда абсолютная величина оказывается недостаточной для формулировки обоснованных выводов о масштабах явления, его размерах, насыщенности, плотности распространения. Так, например, для определения уровня обеспеченности населения легковыми автомобилями рассчитывается число автомашин, приходящихся на 100 семей, для определения плотности населения рассчитывается число людей, приходящихся на 1 кв.км. Так, по данным социальной статистики на начало мая 2006г. численность граждан, состоящих на учете в службе занятости, составляла 3064 тыс. человек, а число заявленных предприятиями вакансий - 309 тыс. Отсюда следует, что на каждых 100 незанятых приходилось 10 свободных мест (309:3064*100). Относительный показатель сравнения представляет собой соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия, фирмы, районы, области, страны и т.п.): 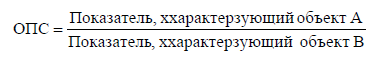 Для выражения данного показателя могут использоваться как коэффициенты, так и проценты. Урок 15 Степенные средние величины в статистике План 1. Понятие средних величин 2. Виды средних величин Задание для студентов: Учебник «Статистика», В.С. Мхитарян с.58-87 , Задачи из сборника 1. Понятие средних величин Общественные явления, несмотря на наличие многочисленных и разнообразных уровней или значений, обладают некоторыми характерными, свойственными большинству из них свойствами, которые могут выражаться в статистике при помощи средних величии. Средние величины в статистике — это показатели, выражающие характерные, типичные, свойственные большинству признаков размеры и соотношения. Метод средних величин заключается в замене большого числа фактических значений признака одной усредненной величиной, поглощающей имеющиеся внутри совокупности вариации. Надежность средних величин зависит как от меры, величины вариации признака внутри совокупности, так и от численности самой совокупности. Чем меньше вариация признака и больше совокупность, по которой она определяется, тем надежнее средняя величина. Поэтому в статистике разработаны как правила использования метода средних величин, гак и правила расчета средних величии. Прежде всего, средние величины должны рассчитываться для качественно однородных совокупностей. Только в этом случае средняя сохраняет свое свойство выражать характерные особенности изучаемых явлений. Далее, общие средние для качественно однородных явлений должны дополняться средними и индивидуальными величинами, характеризующими части целого. И, наконец, средние должны рассчитываться для достаточно многочисленных совокупностей, чтобы в них мог проявиться закон больших чисел, обеспечивающий устойчивость средних. 2. Виды средних величин В статистике используются различные виды средних величин: средняя арифметическая, средняя гармоническая, средняя геометрическая, средняя квадратическая, средняя хронологическая и т. д. При использовании средних величин важно правильно выбрать вид средней и способ ее расчета. Самой распространенной средней, используемой в социально-экономическом анализе, является средняя арифметическая. Средние арифметические бывают простые и взвешенные. Средняя арифметическая простая рассчитывается по формуле: 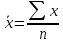 , ,где х _ индивидуальные значения признака, средняя величина которых находится; п - количество единиц совокупности. Средняя арифметическая простая применяется в тех случаях, когда каждое индивидуальное значение признака встречается один раз или одинаковое число раз. Например, чтобы определить средний возраст трех студентов: 17, 18 и 19 лет или средний возраст 30 студентов, если среди них семнадцати-, восемнадцати- и девятнадцатилетних студентов по 10, следует (в обоих случаях) суммировать возраст студентов и разделить на 3: 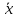 = (17 +18 +19)/3 = 18 (лет). = (17 +18 +19)/3 = 18 (лет).Если же варианты (значения признака) встречаются неодинаковое число раз, то используется средняя арифметическая взвешенная: 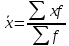 Где 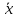 — варианты, значения признака; f — частота появления — варианты, значения признака; f — частота появлениясоответствующего значения признака. Например, нужно определить средний возраст 30 студентов, если среди них пять семнадцати летних, 15 — во- семнадцатилетних и 10 - девятнадцатилетних. Воспользовавшись формулой, получим: 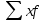 =17x5 + 18x15 + 19x10 (года). =17x5 + 18x15 + 19x10 (года).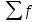 =30 =30Таким образом, для расчета средней арифметической взвешенной необходимо иметь ряд индивидуальных значении признака и частоту каждой из вариант. В некоторых случаях средняя рассчитывается по другому: когда известен ряд вариант (х) и ряд произведений вариант на частоту (x*f), а сама частота f неизвестна. В этом случае средняя рассчитывается по формуле средней гармонической взвешенной: 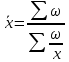 , ,где 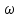 =xf =xfНапример, следует определить среднюю заработную плату работников трех магазинов, если фонд заработной пла- ты в первом из них 1560, во втором — 1647, в третьем 1848 тыс. руб., а заработная плата одного работника 15,2, 16,1 и 12,6 тыс. руб. соответственно. Для того чтобы определить среднюю заработную плату одного работника по трем магазинам, надо общин фонд заработной платы разделить па численность работников утих магазинов. Фонд заработной платы известен ( 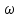 ), а численности (f) нет, по се можно найти делением фонда ), а численности (f) нет, по се можно найти делением фондапо каждому магазину на заработную плату одного работника. Расчет величины средней заработной платы будет иметь такой вид: 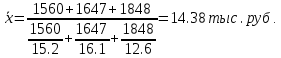 Выбор той или пион формулы расчета средней величины зависит только от характера связей между элементами исходных данных, т. е. от имеющейся информации. Средняя гармоническая может иметь и простую форму расчета, которая в практике статистики используется крайне редко и представляет собой простую среднюю из обратных значений признака. Например, в бригаде работает два человека, которые производят одни и те же детали. При этом первый рабочий затрачивает на производство одной детали 2мин., второй — 6 мин. Нужно определить средние затраты времени на производство одной детали. Применим формулу средней гармонической простой: 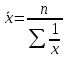 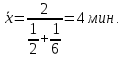 Из приведенных примерных расчетов средних величин видно, что их величина зависит как от индивидуальных значении признака в случае использования простых видов средних величии, так и от удельного веса этих значений в общей совокупности при использовании взвешенных видов. Еще одной формулой, по которой может осуществляться расчет среднего показателя, является средняя геометрическая. Сначала обратимся к формуле средней геометрической простой Она выглядит следующим образом: 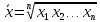 Соответственно средняя геометрическая взвешенная приобретает следующее выражение: 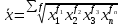 Наиболее широкое применение этот вид средней получил в анализе динамики для определения среднего темпа роста. В основе вычислений ряда сводных расчетных показателей лежит средняя квадратическая. Формула невзвешенной средней квадратической достаточно проста: 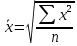 Взвешенная средняя квадратическая: 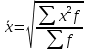 Наиболее широко этот вид средней используется при расчете показателей вариации. Урок 17 Структурные средние: мода, медиана Задание для студентов: Учебник «Статистика» В.С. Мхитаряна стр.112-116 Курс лекций Челпанова Р.Н Стр. 70 Наиболее часто используемыми в экономической практике структурными характеристиками являются мода и медиана. Мода представляет собой значение изучаемого признака, повторяющееся с наибольшей частотой. Медианой называется значение признака, приходящееся на середину ранжированной (упорядоченной) совокупности. Определим моду и медиану по несгруппированным данным. Предположим, что 9 торговых фирм города реализуют товар А по следующим оптовым ценам (тыс. руб.): 4,4; 4,3; 4,4; 4,5; 4,3; 4,3; 4,6; 4,2; 4,6. Как видим, чаще всего встречается цена 4,3 тыс. руб. Она и будет модальной. Для определения медианы необходимо провести ранжирование приведенного цифрового ряда: 4,2; 4,3; 4,3; 4,3; 4,4; 4,4; 4,5; 4,6; 4,6. Центральной в этом ряду является цена 4,4 тыс. руб. Следовательно, данная цена и будет медианой. Если ранжированный ряд включает четное число единиц, то медиана определяется как средняя из двух центральных значений. Теперь рассмотрим определение моды и медианы по сгруппированным данным (рядам распределения). Предположим, распределение торговых предприятий города по уровню розничных цен на товар А имеет следующий вид:
Определение моды по дискретному вариационному ряду не составляет большого труда - наибольшую частоту (60 предприятий) имеет цена 55 руб., следовательно, она и является модальной. Для определения медианного значения признака по следующей формуле находят номер медианной единицы ряда: 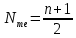 где n - объем совокупности. В нашем случае 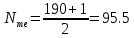 Полученное дробное значение, всегда имеющее место при четном числе единиц в совокупности, указывает, что точная середина находится между 95 и 96 предприятиями. Необходимо определить, в какой группе находятся предприятия с этими порядковыми номе- рами. Это можно сделать, рассчитав накопленные частоты. Очевидно, что магазинов с этими номерами нет в первой группе, где всего лишь 12 торговых предприятий, нет их и во второй группе (12 + 48 = 60). Что касается 95-го и 96-го предприятий, то они находятся в третьей группе (12 + 48 + 56 = 116) и, следовательно, медианой является цена 54 руб. В отличие от дискретных вариационных рядов определение моды и медианы по интервальным рядам требует проведения определенных расчетов на основе следующих формул. Первая из них: 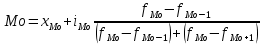 где 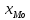 - нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); - нижняя граница модального интервала (модальным называется интервал, имеющий наибольшую частоту); 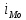 - ширина модального интервала; - ширина модального интервала; 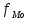 - частота модального интервала; - частота модального интервала; 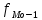 - частота интервала, предшествующего модальному; - частота интервала, предшествующего модальному; 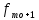 - частота интервала, следующего за модальным. - частота интервала, следующего за модальным.Вторая: 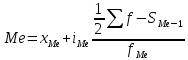 где 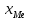 - нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); - нижняя граница медианного интервала (медианным называется первый интервал, накопленная частота которого превышает половину общей суммы частот); 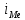 - ширина медианного интервала; - ширина медианного интервала;  - накопленная сумма частот интервалов, предшествующих медианному интервалу; - накопленная сумма частот интервалов, предшествующих медианному интервалу; 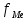 – частота медианного интервала. – частота медианного интервала.Урок 19 Показатели вариации План 1.Понятие и виды показателей вариации 2. Методика расчета показателей вариации Задание для студентов: Учебник «Статистика» В.С. Мхитаряна стр 116-119 1.Понятие и виды показателей вариации Вариация — это различия индивидуальных значений признака у единиц изучаемой совокупности. Исследование вариации имеет большое практическое значение и является необходимым звеном в экономическом анализе. Необходимость изучения вариации связана с тем, что средняя, являясь равнодействующей, выполняет свою основную задачу с разной степенью точности: чем меньше различия индивидуальных значений признака, подлежащих осреднению, тем однороднее совокупность, а, следовательно, точнее и надежнее средняя, и наоборот. Следовательно по степени вариации можно судить о границах вариации признака, однородности совокупности по данному признаку, типичности средней, взаимосвязи факторов, определяющих вариацию. Изменение вариации признака в совокупности осуществляется с помощью абсолютных и относительных показателей. Абсолютные показатели вариации включают: - размах вариации R; - среднее линейное отклонение - дисперсию - среднее квадратическое отклонение - коэффициент вариации v. 2. Методика расчета показателей вариации Размах вариации — это разность между максимальным и минимальным значениями признака. 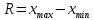 Он показывает пределы, в которых изменяется величина признака в изучаемой совокупности. Пример: Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет. Решение: размах вариации = 9 — 2 = 7 лет. Среднее линейное отклонение Среднее линейное отклонение простое: 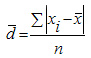 Опыт работы у пяти претендентов на предшествующей работе составляет: 2,3,4,7 и 9 лет. В нашем примере: 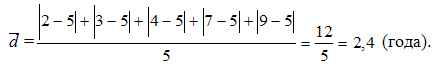 Ответ: 2,4 года. Среднее линейное отклонение взвешенное применяется для сгруппированных данных: 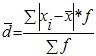 Среднее линейное отклонение в силу его условности применяется на практике сравнительно редко (в частности, для характеристики выполнения договорных обязательств по равномерности поставки; в анализе качества продукции с учетом технологических особенностей производства). Среднее квадратическое отклонение Наиболее совершенной характеристикой вариации является среднее квадратическое откложение, которое называют стандартом (или стандартным отклонение). Среднее квадратическое отклонение ( Среднее квадратическое отклонение простое: 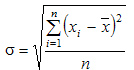 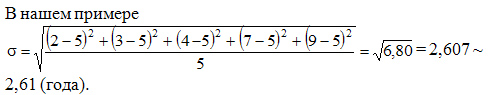 Среднее квадратическое отклонение взвешенное применяется для сгруппированных данных: 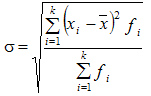 Между средним квадратическим и средним линейным отклонениями в условиях нормального распределения имеет место следующее соотношение: Среднее квадратическое отклонение, являясь основной абсолютной мерой вариации, используется при определении значений ординат кривой нормального распределения, в расчетах, связанных с организацией выборочного наблюдения и установлением точности выборочных характеристик, а также при оценке границ вариации признака в однородной совокупности. Дисперсия Дисперсия простая: 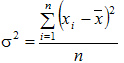 В нашем примере: Дисперсия взвешенная: 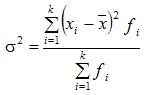 Коэффициент вариации - наиболее часто применяемый показатель относительной колеблемости, характеризующий однородность совокупности. Совокупность считается однородной, если коэффициент вариации не превышает 33 % для распределений, близких к нормальному. 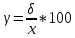 |