Статистика. Курс лекций Статистика. Урок Введение. Предмет, метод, задачи статистики План
 Скачать 469.82 Kb. Скачать 469.82 Kb.
|
|
Раздел 6. Урок 21 Ряды динамики в статистике План 1. Понятие рядов динамики 2. Виды рядов динамики Задание для студентов: Учебник «Статистика» В.С. Мхитаряна стр.205-220 Курс лекций Челпанова Р.Н стр. 76-84 1. Понятие рядов динамики Коммерческая деятельность на рынке товаров и услуг развивается во времени. Динамизм социально-экономических явлений есть результат взаимодействия разнообразных причин и условий. Основная цель статистического изучения динамики коммерческой деятельности состоит в выявлении и измерении закономерностей их развития во времени. Это достигается посредством, построения и анализа статистических рядов динамики. Рядами динамики называются статистические данные, отображающие развитие изучаемого явления во времени. В каждом ряду динамики имеются два основных элемента: 1) показатель времени – t; 2) соответствующие им уровни развития изучаемого явления - у. В качестве показаний времени в рядах динамики выступают либо определенные даты (моменты) времени, либо отдельные периоды (годы, кварталы, месяцы, сутки). Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами. 2. Виды рядов динамики В зависимости от характера изучаемого явления уровни рядов динамики могут относиться или к определенным датам (моментам) времени, или к отдельным периодам. В соответствии с этим ряды динамики подразделяются на моментные и интервальные. Моментные ряды динамики отображают состояние изучаемых явлений на определенные даты (моменты) времени. Пример моментного ряда динамики: Средне списочная численность преподавателей колледжа в 2008-2012 г., чел.
Посредством моментных рядов динамики можно изучить численность студентов, посещаемость занятий, успеваемость и т.д. Интервальные ряды динамики отображают итоги развития изучаемых явлений за отдельные периоды (интервалы) времени. Примером интервального ряда динамики могут служить данные о розничном товарообороте магазина в 2007—2011 гг., тыс.руб:
Особенностью интервального ряда динамики является то, что каждый его уровень складывается из данных за более короткие интервалы (субпериоды) времени. Например, суммируя товарооборот за первые три месяца года, получают его объем за I квартал, а сумма товарооборота четырех кварталов дает объем товарооборота за год и т. д. Свойство суммирования уровней за последовательные интервалы времени позволяет получать ряды динамики более укрупненных периодов. Посредством интервальных рядов динамики в торговле изучается изменение во времени поступления и реализации товаров, суммы издержек обращения и других показателей, отображающих итоги функционирования (развития) изучаемых явлений за отдельные периоды. По полноте, с которой отражается период времени, как в моментных, так и в интервальных рядах динамики, их делят на полные и неполные. В полных рядах динамики одноименные моменты или периоды времени строго следуют один за другим в календарном порядке, а в неполных рядах нет такой строгой хронологической последовательности. Полные ряды называют рядами динамики с равноотстоящими уровнями, а неполные — с не равностоящими уровнями. В зависимости от вида статистических показателей, используемых при изучении явления, ряды динамики подразделяются на ряды динамики абсолютных, относительных и средних величин. Исходными, первоначальными являются ряды динамики абсолютных величин, так как их получают непосредственно при сводке материалов статистического наблюдения. Ряды динамики относительных и средних величии являются производными рядами. Рядами динамики относительных величин являются ряды показателей, характеризующих темпы динамики изучаемого явления, изменение его структуры, интенсивности и т. п.; рядами динамики средних величин — ряды показателей, которые выражают средние значения изучаемого явления за определенные промежутки времени: среднюю выработку продукции па одного работающего, среднюю заработную плату, среднюю урожайность и т. п. Если ряды динамики представлены относительными или средними величинами, их суммирование не имеет смысла. К тому же, если уровни интервальных рядов динамики являются относительными и средними величинами, то при прочих равных условиях они не зависят от длительности периода. Ряды динамики относительных и средних величин используются для характеристики качественных изменений экономики. Урок 22 Показатели изменения уровней рядов динамики План 1. Аналитические показатели ряда динамики и их взаимосвязь 2. Средние показатели ряда динамики Задание для студентов: Учебник «Статистика» В.С. Мхитаряна стр.205-220 , Курс лекций 2007г. Челпанова Р.Н стр. 76-84 1. Аналитические показатели ряда динамики и их взаимосвязь При изучении динамики социально-экономических явлений рассчитывают аналитические показатели: абсолютные приросты, темпы роста и прироста, абсолютное значение одного процента прироста (снижения). Расчет этих показателей основан на абсолютном или относительном сравнении уровней динамического ряда. При этом сравниваемый уровень называется текущим, а тот уровень, с которым сравнивают, — базисным. За базисный уровень обычно принимается либо предыдущий уровень, либо начальный (первый) в данном динамическом ряду. Если сравнивается каждый последующий уровень с предыдущим, получают ценные показатели динамики. Если каждый уровень сравнивается с начальным или каким-либо другим, принятым за постоянную базу сравнения, получают базисные показатели динамики. Абсолютный прирост — это разность двух уровней ряда динамики. Он показывает, на сколько единиц данный уровень больше или меньше уровня, взятого для сравнения, и выражается в тех же единицах, что и уровни динамического ряда. Цепной абсолютный прирост Уц исчисляется как разность между сравниваемым (текущим) уровнем yi и уровнем, который ему предшествует yi-1. Уц = yi yi-1 Базисный абсолютный прирост Уб исчисляется как разность между сравниваемым уровнем yi и уровнем, принятым за постоянную базу сравнения, у0. Уб = yi yо Абсолютный прирост может быть положительной или отрицательной величиной, в последнем случае это снижение. Цепной абсолютный прирост выражает абсолютную скорость роста. Сумма цепных абсолютных приростов за какой-то период времени равна базисному абсолютному приросту за весь этот период. Разность между анализируемым и предыдущим базисными абсолютными приростами дает соответствующий цепной абсолютный прирост. Темп роста это отношение двух уровней ряда динамики. Он показывает, во сколько раз больше (или меньше) или сколько процентов данный уровень составляет по отношению к другому уровню, взятому для сравнения. В первом случае темп роста выражается в коэффициентах, во втором — в процентах. Цепной темп роста Тц исчисляется как отношение между сравниваемым (текущим) yi и предшествующим ему уровнем yi-1 Тц = 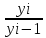 Базисный темп роста Тб исчисляется как отношение между сравниваемым уровнем yi и уровнем, принятым за постоянную базу сравнения, у0: Тц = 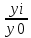 Последовательное произведение цепных темпов роста, выраженных в коэффициентах, за определенный период времени дает базисный темп роста за этот же период. Отношение анализируемого базисного темпа роста к предыдущему дает соответствующий цепной темп роста. Темп прироста — это отношение абсолютного прироста к уровню, принятому за базу сравнения. Он обычно выражается в процентах и показывает, на сколько процентов уровень данного периода больше (или меньше) базисного. Цепной темп прироста Тц исчисляется как отношение цепного абсолютного прироста Уц к предыдущему уровню yi-1 Тц = 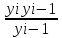 = Тц – 1 (100%) = Тц – 1 (100%)Базисный темп прироста Тб исчисляется как отношение базисного абсолютного прироста Уб к базисному уровню у0: Тб = 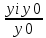 = Тб – 1 (100%) = Тб – 1 (100%)Темп прироста Т вычисляется и как разность между темпом роста Т, выраженным в процентах, и 100%: Т = Т -100%. Темп прироста может быть как положительной, так и отрицательной величиной. В первом случае это свидетельствует о положительной динамике (росте), а во втором — об отрицательной динамике (снижении). Абсолютное значение одного процента прироста Аi% — это отношение абсолютного прироста Уi за определенный период (обычно за год) к темпу прироста Тi. за этот же период, выраженному в процентах. Этот показатель раскрывает, какая абсолютная величина скрывается за относительной - одним процентом прироста. Количественно абсолютное значение одного процента прироста равно одной сотой части уровня, предшествующего анализируемому. Аi%= 0.01 yi-1 Если в исследуемый период наблюдалось снижение, а не рост явления, характеризуемого рядом динамики, то рассчитывается соответственно абсолютное значение одного процента не прироста, а снижения. Выражается абсолютное значение одного процента прироста (или снижения) в единицах измерения уровней анализируемого ряда динамики. 2. Средние показатели ряда динамики Уровни и аналитические показатели рядов динамики изменяются во времени. Поэтому для получения обобщающей характеристики динамики социально-экономических явлений широко используются средние величины: средний уровень, средний абсолютный прирост, средний темп роста и прироста. Средний уровень ряда динамики характеризует типичную величину абсолютных уровней. Методы расчета среднего уровня интервального и моментного рядов динамики разные. Средний уровень из абсолютных уровней для интервальных рядов динамики рассчитывается по формуле средней арифметической: 1. При равных интервалах используют среднюю арифметическую простую: 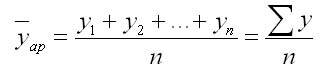 где у — абсолютные уровни ряда; n — число уровней ряда. 2. При неравных интервалах используют среднюю арифметическую взвешенную: 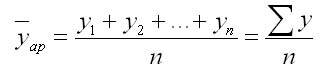 где у1,...,уn — уровни ряда динамики; t1,... tn — веса, длительность интервалов времени. Средний уровень моментного ряда динамики рассчитывается по формуле: 1. С равностоящими уровнями рассчитывается по формуле средней хронологической моментного ряда: 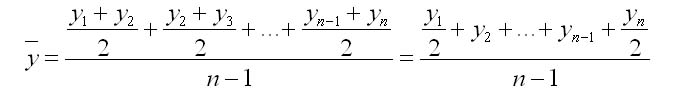 ¶где у1,...,уn — уровни периода, за который делается расчет; n — число уровней; ¶где у1,...,уn — уровни периода, за который делается расчет; n — число уровней;n-1 — длительность периода времени. 2. С неравностоящими уровнями рассчитывается по формуле средней хронологической взвешенной: ¶ 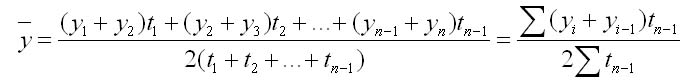 где у1,...,уn — уровни рядов динамики; t — интервал времени между смежными уровнями Средний абсолютный прирост определяется как среднее из абсолютных приростов за равные промежутки времени одного периода. Он рассчитывается по формулам: 1. По цепным данным об абсолютных приростах за ряд лет рассчитывают средний абсолютный прирост как среднюю арифметическую простую: 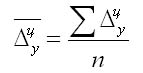 где n — число степенных абсолютных приростов в исследуемом периоде. 2. Средний абсолютный прирост рассчитывают через базисный абсолютный прирост в случае равных интервалов 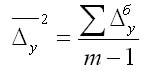 где m — число уровней ряда динамики в исследуемом периоде, включая базисный. Средний темп роста есть свободная обобщающая характеристика интенсивности изменения уровней ряда динамики и показывает, во сколько раз в среднем за единицу времени изменяется уровень ряда динамики. В качестве основы и критерия правильности вычисления среднего темпа роста (снижения) применяется обобщающий показатель, который рассчитывается как произведение цепных темпов роста, равное темпу роста за весь рассматриваемый период. Если значение признака образуется как произведение отдельных вариантов, то используют среднюю геометрическую. Так как средний темп роста представляет собой средний коэффициент роста, выражен в процентах, то для равностоящих рядов динамики расчеты по средней геометрической сводятся к вычислению средних коэффициентов роста из цепных по «цепному способу»: 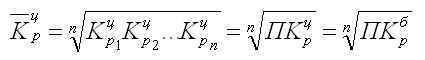 где n — число цепных коэффициентов роста; Кц — цепные коэффициенты роста; Кб — базисный коэффициент роста за весь период. Определение среднего коэффициента роста может быть упрощено, если будут ясны уровни динамического ряда. Так как произведение цепных коэффициентов роста равно базисному, то в подкоренное выражение подставляют базисный коэффициент роста. Формула для определения среднего коэффициента роста для равностоящих рядов динамики по «базисному способу» будет такая: 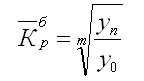 Средние темпы прироста рассчитываются на основе средних темпов роста (Тр) вычитанием из последних 100%: Для того чтобы определить средний коэффициент прироста (Кпр), нужно из значений коэффициентов роста (Кр) вычесть единицу |
