Пояснительная (Куликов). В данном курсовом проекте проектируется железобетонный мост под железную дорогу через постоянный водоток
 Скачать 0.71 Mb. Скачать 0.71 Mb.
|
|
2.2 Расчёт главной балки. 2.2.1 Определение нормативных постоянных нагрузок. В отличие от нагрузок, принимаемых для расчета плиты балластного корыта, в данном расчете примем нагрузку от собственного веса конструкций пролетного строения, приходящуюся на 1 м длины двух балок, кН/м: 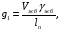 (2.36) где Vжб – объем железобетонного пролетного [1] прил.В. 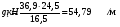 Другие постоянные нагрузки - g2 – вес двух тротуаров с перилами, равный 5,4 кН/м; g3=38,8 кН/м - вес балласта с частями пути. Изм. Лист № докум. Подпись Дата Лист 35 2.2.2 Построение линий влияния изгибающих моментов и поперечных сил. Определение нормативных временных вертикальных нагрузок. Нормативную временную вертикальную нагрузку принимаем в соответствии с длинами загружений линий влияния (см. рис. 2.3) и данными [1] прил. Н при 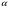 = 0,5 независимо от положения вершины линии влияния, т.к. путь устроен на балласте: = 0,5 независимо от положения вершины линии влияния, т.к. путь устроен на балласте: Вычислим необходимые для дальнейших расчетов площади линий влияния: 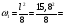 31,21 м2 31,21 м2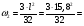 23,40 м2 23,40 м2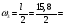 7,9 м2 7,9 м2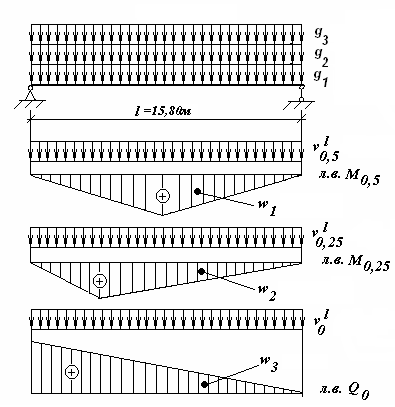 Рис. 2.3 Линии влияния 2.2.3 Определение расчетных внутренних усилий для расчетов на прочность, выносливость и трещиностойкость. Определим коэффициенты для нагрузок, которые понадобятся для дальнейших расчётов:
Изм. Лист № докум. Подпись Дата Лист 36 (1+μ) и (1+2/3μ) – динамические коэффициенты для расчета соответственно по прочности и выносливости ([2]). 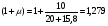 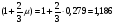 Определим расчетные усилия:
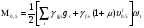 (2.37) 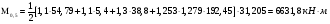 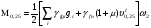 (2.38) 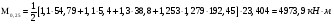 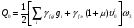 (2.39) 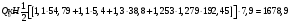
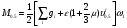 (2.40) 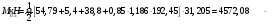
по образованию продольных трещин: Изм. Лист № докум. Подпись Дата Лист 37 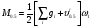 (2.41) 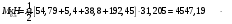 по раскрытию нормальных трещин: 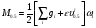 (2.42) 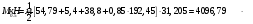 по ограничению касательных напряжений: 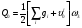 (2.43) 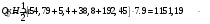 по раскрытию наклонных трещин: 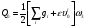 (2.44) 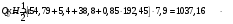 2.2.4 Назначение расчётного сечения балки и подбор рабочей арматуры в середине пролёта. Основные размеры сечения главной балки заданы преподавателем (см. П.2.1.1) и дополнены, исходя из принятых на практике и рекомендуемых в литературе данных ([1] прил.В). Сечение главной балки чаще принимаем тавровым. Расстояние между осями балок принимаем равным 1800 мм. Для расчета в курсовом проекте фактическое поперечное сечение пролетного строения заменяем на сечение упрощенной формы (см. рис. 2.4). Приведенная толщина плиты может быть определена по формуле: 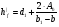 (2.45) (2.45)где Аh –площадь вутов, Ah  0,0142 м2 (вычислено на ЭВМ, при помощи AutoCAD) (см.рис.2.4). 0,0142 м2 (вычислено на ЭВМ, при помощи AutoCAD) (см.рис.2.4).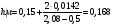 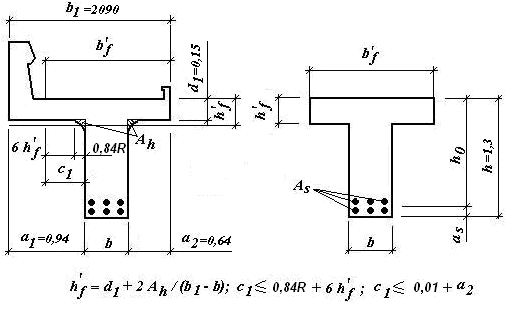 Изм. Изм.Лист № докум. Подпись Дата Лист 38 Рис. 2.4 Расчётные размеры главной балки Далее зададимся рабочей высотой сечения: 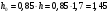 м. м.Определим длину свесов: c1 ≤ 0.9R+6h’f; c2 ≤ 0.9R+a2; с1≤ 1,278; с2≤0,91. Примем длину свеса С= 0,91 м. В первом приближении определяем требуемую площадь рабочей (растянутой) арматуры из условия: 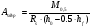 (2.46) 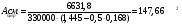 Зададимся диаметром арматуры: d = 40, тогда А1=12,56 см2. Требуемое количество стержней в нижнем поясе балки определим по формуле: 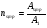 (2.47) (2.47)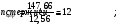 Исходя из дальнейших расчётов на ЭВМ мы примем 17 стержней. Фактическое значение площади всей арматуры в растянутой зоне будет равно: Аs,ф=А1 · ns=17·12,56 = 213,52 см2. Составляем схему размещения арматурных стержней в нижнем поясе балки (см. рис.2.5). Арматурные стержни располагаем симметрично относительно вертикальной оси балки. Назначаем толщину защитного слоя бетона: Сб=3см. В вертикальных рядах арматуру размещаем пучками по 3 стержня без просветов. Изм. Лист № докум. Подпись Дата Лист 39 Расстояние в свету между вертикальными рядами арматуры Сп=6 см (при расположении арматуры в пять рядов). Затем вычисляем расстояние от центра тяжести сечения растянутой арматуры до нижней грани балки: as = ∑niai / ns, (2.48) где ni – количество стержней в i – м ряду; ai – расстояние от оси i – го ряда до нижней грани балки. 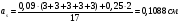 После этого уточняем рабочую высоту сечения h0 = h – as =1,7-0,1088 =1,59 м. 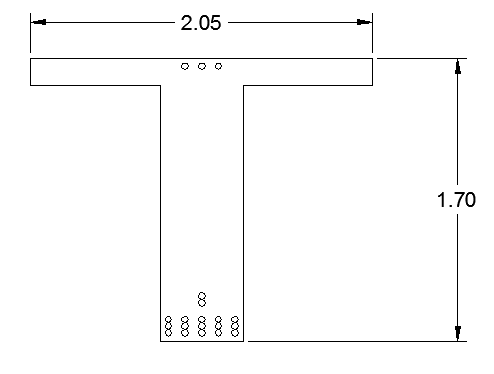 Рис. 2.5 Схема расположения стержней арматуры в нижнем поясе балки. 2.2.5 Расчет балки на прочность нормального сечения в середине пролета. Проверим следующее условие: (2.49) 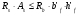 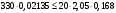 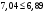 Изм. Лист № докум. Подпись Дата Лист 40 Условие выполняется, значит нейтральная ось проходит в пределах высоты плиты (рис. 2.6) и сжатая зона сечения балки имеет прямоугольную форму. Высоту сжатой зоны определим по формуле: 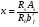 (2.50) 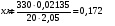 Проверим условие: = х/h0 ≤ y = (0,85 – 0,008 Rb) / (1 + 0,0001Rs(4,545 – 0,145Rb). Здесь Rb и Rs принимаем в МПа. y = (0,85 – 0,008·20) / (1 + 0,0001· 330· (4,545 – 0,145· 20))=0,654 Изм. Лист № докум. Подпись Дата Лист 41 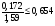 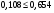 Условие выполняется. Далее проверим прочность нормального сечения по следующей формуле: 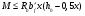 (2.51) (2.51)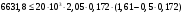 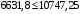 Условие выполняется. 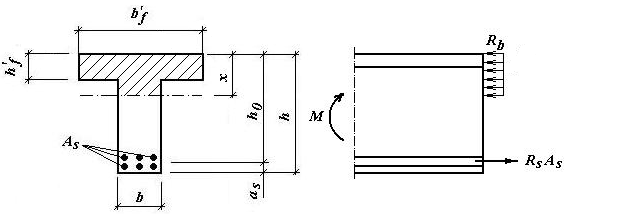 Рис. 2.6 Схема к расчёту нормального сечения в середине пролёта 2.2.6 Расчет балки на выносливость нормального сечения в середине пролета. В расчетах на выносливость принимаем, что растянутый бетон полностью выключился из работы сечения и все растягивающее усилие воспринимается арматурой (см. рис. 2.7). В этом случае наибольшие напряжения в бетоне и арматуре балки определим по формулам: 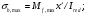 (2.52) (2.52) 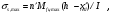 (2.53) Изм. Лист № докум. Подпись Дата Лист 42 где Mf,max – изгибающий момент для расчетов на выносливость (см. формулу (4.24)); hu – расстояние от крайнего ряда растянутой арматуры до сжатой грани (hu=1,67). В результате расчета на выносливость выясним выполнимость двух условий: 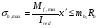 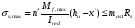 (2.54) (2.54) (2.55) где 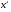 - высота сжатой зоны - высота сжатой зоныIred - приведенный момент инерции 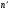 - отношение модуля упругости арматуры к модулю упругости бетона (для бетона В40 n’=10). - отношение модуля упругости арматуры к модулю упругости бетона (для бетона В40 n’=10).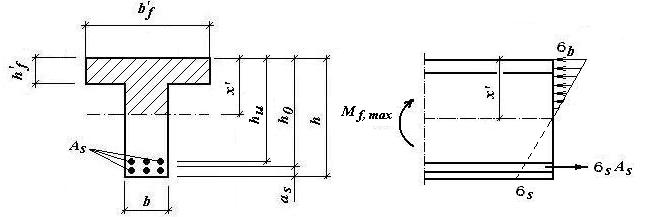 Рис. 2.7 Схема к расчёту балки на выносливость. Для определения расчётных сопротивлений бетона и арматуры вычислим характеристики цикла повторяющихся напряжений по формуле: ρb = ρs = Mf,min / Mf,max, (причём значения Mf,min и Mf,max определим по формуле 2.43). ρb = ρs =1619,161/4648,633 = 0,348, значит εb =1,124, εps = 0,829 ([1] прил.М). mb1 = 0,6·1,34·1,124 = 0,904 (см. формулу 2.30); mas1 = 1· 0,829 = 0,829 (см. формулу 2.33). Высота сжатой зоны х’: 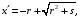 (2.56) где 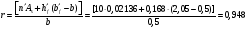 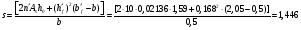 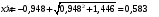 Приведённый момент инерции: (2.57) Изм. Лист № докум. Подпись Дата Лист 43 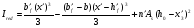 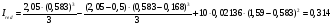 а) выносливость по бетону: 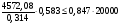 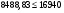 Условие выполняется. б) выносливость по арматуре: 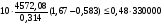 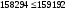 Условие выполняется. 2.2.7 Расчет балки на трещиностойкость нормального сечения в середине пролета. Расчёт по образованию продольных трещин: 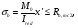 (2.58) где М0– момент от нормативных постоянных и временных нагрузок в середине пролёта. Rb,mc2 =19600 кПа- расчётное сопротивление бетона класса В40 осевому сжатию на стадии эксплуатации [2]. 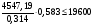 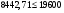  Условие выполняется. Расчёт по раскрытия трещин: 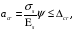 (2.59) где σs= 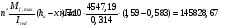 Es=1,96·106 мПа - модуль упругости арматуры класса А-III ([1] прил.М); Ψ – коэффициент раскрытия трещин: при арматуре периодического профиля Ψ=13,59 (см.2.1.9) т.к. Ar=b(h-x’)=50  (170-58,3)=5585 см2, R=Ar/nd=5585/1· 17· 4,0=82,13 см. (170-58,3)=5585 см2, R=Ar/nd=5585/1· 17· 4,0=82,13 см. 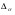 - предельное значение расчетной ширины раскрытия трещин принимается не более 0,020 см [2]. - предельное значение расчетной ширины раскрытия трещин принимается не более 0,020 см [2].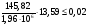 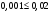 Изм. Лист № докум. Подпись дпись Дата Лист 44 Условие выполняется. 2.2.8 Построение эпюры материалов с определением мест отгибов рабочей арматуры. Для определения мест отгибов рабочей арматуры строим огибающую эпюру максимальных моментов в балке. 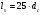 Начало отгибов продольных растянутых стержней арматуры располагаем за сечением, в котором стержни учитываются с полным расчётным сопротивлением. Длину заводки за сечение для арматуры стали класса АIII и бетона класса В40 определяем по формуле: Начало отгибов продольных растянутых стержней арматуры располагаем за сечением, в котором стержни учитываются с полным расчётным сопротивлением. Длину заводки за сечение для арматуры стали класса АIII и бетона класса В40 определяем по формуле:(2.60) 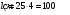 Построение эпюры материалов, а также определение мест отгибов рабочей арматуры ведём в соответствии с требованиями [2]:
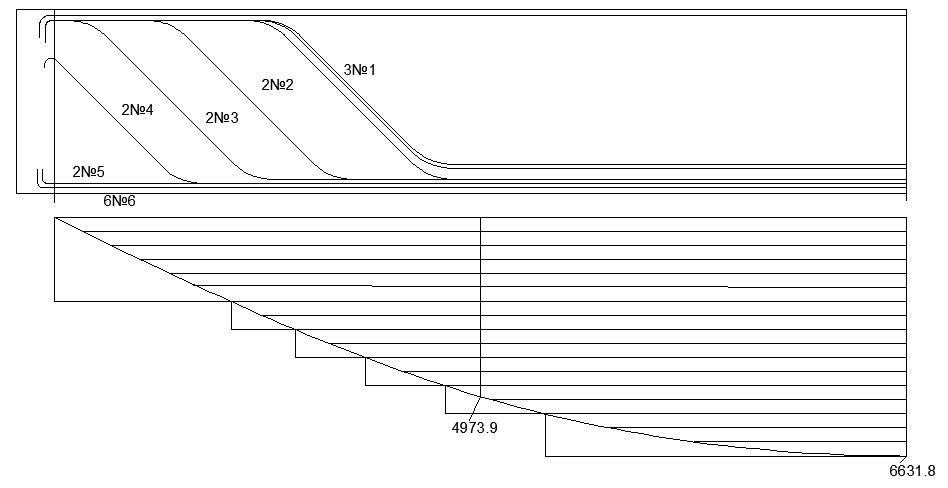 Рис. 2.6 Схема для расстановки наклонных стержней Изм. Лист № докум. Подпись Дата Лист 45 2.2.9 Определение прогиба балки в середине пролёта Прогиб в середине пролета определяем по формуле: 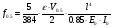 (2.61) (2.61)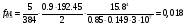 Проверим выполнение условия: 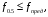 где 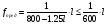 (2.62) (2.62)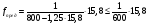 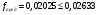 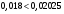 Условие по ограничению прогиба в середине пролета выполняется. |

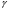 f - коэффициенты надежности по нагрузкам [2], для постоянных нагрузок:
f - коэффициенты надежности по нагрузкам [2], для постоянных нагрузок: