Луцык В.И. Конструирование многокомпонентных систем. В. И. Луцык конструирование многокомпонентных систем. I. Txy диаграммы с 25ю поверхностями учебнометодическое пособие
 Скачать 1.53 Mb.
|
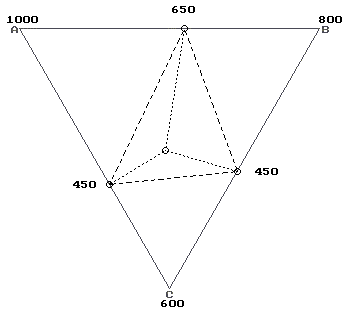
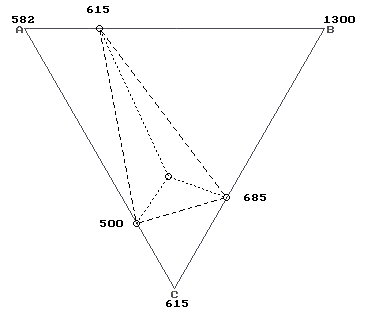
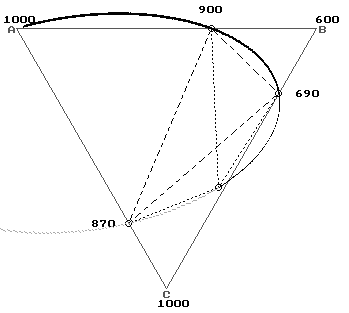
E Q P Ee е e е e e e p Eeee Qeee Peee Eep>e e e e e  Q Q P P e p e p e p e p Qep>e Qp>ee Pp>ee Pep>e  p p p pE Q P E e p e p e p e p Ep>p>e Qp>p>e Pp>p>e Ep>  p p p pQ Q P e p e p e p e P p Qep> Qp> e Pep> Pp> p p p p  E Q P E e p e p e p p p E e Q e P p>e E p p p p  Q Q P P p p p p p p p p Q Q p> P p> Pp> Рис. 11. Подтипы ФД с бинарными (е,р) и тройной (Е,Q,P) точками 23 О 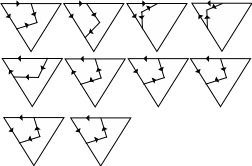 возможности линейной аппроксимации для 10 видов поверхностей ликвидуса (рис. 12) судим по свойствам их периметра: - у вариантов а), е), з) должно быть ромбовидное строение с противолежащими углами одного типа (либо тупыми, либо острыми); - варианты в), г) не должны быть выпуклыми; - варианты б), д) должны иметь 2 острых соседних угла (трапециевидная фигура). Варианты ж) и и) можно представить только в виде седловинных поверхностей, а вариант к) возможен только в случае винтовой поверхности с двумя различными значениями температур в одной из точек огранения.а) б) в) г) д) е) ж) з) и) к) Рис.12. Варианты периметров поверхности ликвидуса 9.3. Исследование траекторий проекции тройной точки.  15 16 5 6 7A eAB B 14 4 2 8 1 eBC 13 eAC 3 9 12 10 C 11 Рис. 13. Разбиение концентрационного треугольника и примыкающего пространства на сектора 24 Продлив стороны стороны концентрационного треугольника и соединяющие бинарные точки прямые линии, получим деление Х-У проекции ФД и прилегающего к ней пространства на 16 секторов (рис. 13). Исследуем траектории точек пересечения трех плоскостей, задаваемые изменением температурной координаты одной или нескольких двойных точек (рис. 14, табл. 5). Eeee. Тройная точка принадлежит сектору 1. При понижении (температуры) одной из бинарных точек тройная точка переходит через нее в сектора 5,9,13, а при ее повышении уходит в сектора 9,13 через бинарную точку с меньшей или равной температурой. При одновременном симбатном понижении двух бинарных точек тройная идет в сектора 9 и 13 через ту из них, у которой меньшая или равная температура, а при аналогичном повышении – уходит в сектора 5,9,13 через третью точку. При симбатном понижении всех трех бинарных точек тройная точка ассимптотически приближается к линии AeBC, а при повышении уходит в сектор 13 через ту из менее высоких бинарных точек, которая противолежит вершине с промежуточным значением температуры.
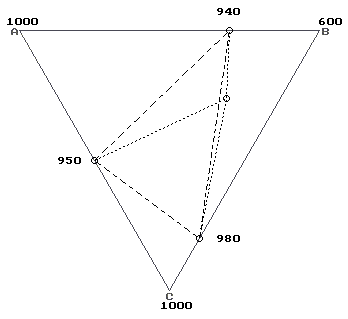
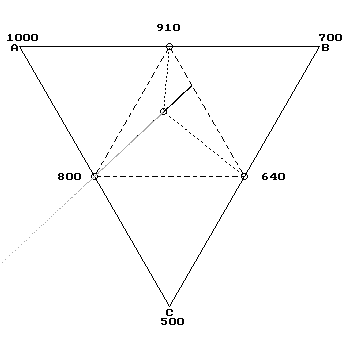
Рис. 14. ФД тройных аддитивных систем Таблица 5. Концентрационные параметры тройных аддитивных ФД (рис. 14)
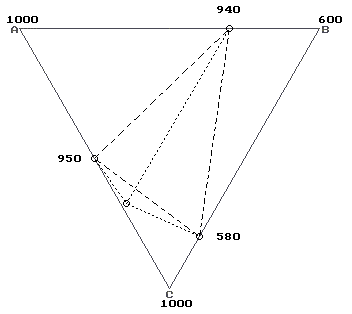
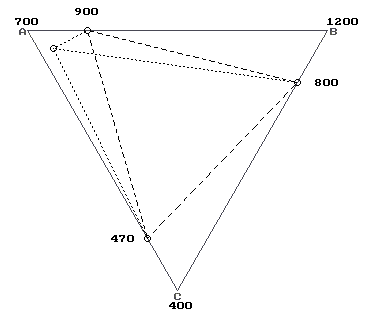
Ep> . Тройная точка принадлежит сектору 2 с двумя перитектиками в его вершинах. При понижении одной из перитектик тройная точка переходит через нее в сектор 3 (внутри Δ) или 16 и проходит затем через эвтектику При понижении бинарной эвтектики тройная ассимптотически приближается к противолежащей вершине треугольника.
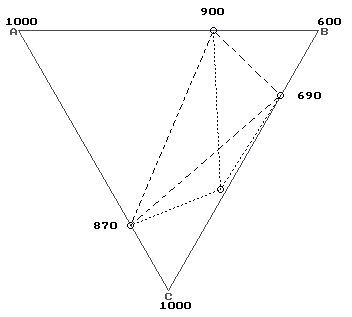
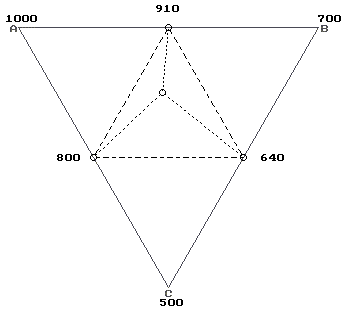
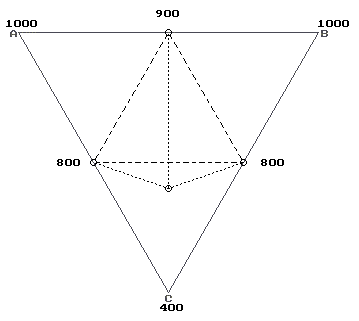
При повышении одной из бинарных перитектик тройная уходит в сектор 10 или 16 через другую перитектику, а при повышении эвтектики уходит через перитектику с большей температурой (в сектор 10). При одновременном повышении одной из перитектик и бинарной эвтектики тройная точка уходит в сектор 10 или 16 через другую перитектику, а при повышении обеих перитектик уходит через перитек- 27 тику с меньшей температурой (в сектор 16). При одновременном понижении любых двух бинарных точек тройная проходит либо через одну из перитектик и эвтектику, либо через сторону треугольника, ограничивающую сектор 2. При симбатном понижении всех трех бинарных точек тройная пересекает линию BC и уходит в сектор 8, а при повышении - проходит через перитектику с наименьшей температурой и уходит в сектор 16. Qep>e. Тройная точка принадлежит сектору 3 с двумя эвтектиками в его вершинах. При понижении одной из эвтектик тройная точка переходит через другую эвтектику и уходит в 8 или 14 сектор, а при ее повышении переходит через нее в сектора 14 и 2. При понижении перитектики тройная точка переходит через эвтектику с большей температурой в сектор 14, а при ее повышении асимптотичес ки приближается к одной из вершин треугольника, являющегося также вершиной сектора 3. При одновременном понижении одной из эвтектик и перитектики тройная точка переходит через другую эвтектику в сектора 8,14, а при понижении двух эвтектик проходит через меньшую. При одновременном повышении двух бинарных точек тройная проходит через сторону AC в сектор 12, если одна из изменяемых точек является принадлежащей этой стороне эвтектикой, иначе тройная точка проходит через бинарные точки, не принадлежащие этой стороне. При симбатном понижении всех трех бинарных точек тройная пересекает линию AC и уходит в сектор 12, а при их повышении - проходит через принадлежащую этой стороне эвтектику и уходит в сектор 14.
В остальных типах диаграмм для характеристики траекторий точек пересечения трех плоскостей, заданные тремя точками на ребрах и тремя точками на гранях тригональной призмы, ограничимся их схемами и некоторыми рисунками (рис. 15): Qep> . 28
Рис. 15. Траектории точек Qep> - при изменении pBC (а) и P p> - при изменении pAB и pBC (б) Q e.
Q . 29
P p> .
Pep> .
Исследование поведения тройной точки показало, что в зависимости от расположения точки пересечения трех плоскостей вне или внутри первого сектора (рис. 13), не противоречащие физическому смыслу траектории ее движения (с положительными барицентрическими координатами) остаются в пределах сектора 1 или одного из трех секторов типа IeIJeIK. Траектории тройной точки имеет вид кривой второго порядка (для тройных точек вне сектора 1 это эллипс). Положение тройной точки в или вне сектора 1 не зависит от ее температурного расположения относительно бинарных точек. Но для каждого топологического типа диаграммы, определяемого взаимным 30 расположением бинарных и тройной точек и вершин концентрационного симплекса, существует свое зафиксированное место тройной точки по отношению к сектору 1. Причем, если продолжить стороны сектора, внутри которого лежит тройная точка, вне концентрационного треугольника ABC, то траектории тройной точки будут лежать между продолжениями этих сторон. Траектории тройной точки при изменении температурной координаты одной бинарной точки обязательно проходят либо через бинарные точки, либо через бинарную точку и вершину концентрационного симплекса. При изменении координат нескольких бинарных точек они могут также проходить как через границы сектора 1, так и через вершины и стороны концентрационного треугольника. Если траектория тройной точки проходит через двойную, то существует продолжение траектории вне концентрационного треугольника. В случае, когда траектория изменяется в направлении границы сектора 1, то по мере такого приближения неограниченно возрастает температурная координата и пересечение со стороной треугольника невозможно и в бесконечности. В пределах одного топологического типа существуют определен ные разрешенные температурные интервалы для бинарных точек. Выход бинарной точки за границы подобного интервала не только изменяет топологический тип диаграммы, но и может привести к смещению тройной точки за пределы концентрационного треугольника. При большом перепаде температур в одной из бинарных систем тройная точка лежит вне концентрационного треугольника. При изменении температурной координаты точек на сторонах или в вершинах концентрационного треугольника может получиться переход от одного топологического типа Т-х-у диаграммы к другой, обычно сопровождающийся резким скачком температурной координаты тройной точки. 10. МОДЕЛИРОВАНИЕ ПОВЕРХНОСТЕЙ ФД КОСОЙ ПЛОСКОСТЬЮ 10.1. Плоскость как частный случай линейчатой поверхности. 10.1.1. Вывод нормального уравнения плоскости, заданной в координатном виде. Точки P, Q, R, S заданы на серединах ребер тетраэдра (рис. 16, слева). Убедимся, что они принадлежат одной плоскости. Нормальный вид ее уравнения должен быть единым, а координатный может 31 зависеть от выбранных точек. Таблица 6. Координаты вершин тетраэдра, плоскости  , косой плоскости  и образующих отрезков  ,  ,  ,  (рис. 16)
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
/2
/12
/6
