Луцык В.И. Конструирование многокомпонентных систем. В. И. Луцык конструирование многокомпонентных систем. I. Txy диаграммы с 25ю поверхностями учебнометодическое пособие

• Название: В. И. Луцык конструирование многокомпонентных систем. I. Txy диаграммы с 25ю поверхностями учебнометодическое пособие
• Анкор: Луцык В.И. Конструирование многокомпонентных систем
• Дата: 13.12.2021
• Размер: 1.53 Mb.
• Имя файла: evt3.doc
• Тип: Учебно-методическое пособие; #301297
• страница: 1 из 5

МИНИСТЕРСТВО ОБРАЗОВАНИЯ

РОССИЙСКОЙ ФЕДЕРАЦИИ

БУРЯТСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

В.И. ЛУЦЫК

КОНСТРУИРОВАНИЕ

МНОГОКОМПОНЕНТНЫХ СИСТЕМ.

I. T-X-Y ДИАГРАММЫ С 25-Ю ПОВЕРХНОСТЯМИ

Учебно-методическое пособие


УЛАН-УДЭ

ИЗДАТЕЛЬСТВО БУРЯТСКОГО ГОСУНИВЕРСИТЕТА

2000
УДК 541.123.3

Л869
Утверждено к печати

редакционно-издательским советом

Бурятского государственного университета
Рецензенты:

доктор физ.-мат. наук Ю.Л. Ломухин

кандидат физ.-мат. наук Г.А.Шишкин

Луцык В.И.

Л869 Конструирование многокомпонентных систем.

I. T-X-Y диаграммы с 25-ю поверхностями.  Улан-Удэ: Издательство Бурятского госуниверситета, 2000.  40 с.

ISBN 5-85213-301-9

Учебно-методическое пособие рекомендуется студентам математических, физических, химических и геологических специальностей университетов, выполняющих учебные и исследовательские задания (интеграционные курсовые и дипломные работы) по моделированию фазовых диаграмм многокомпонентных систем с использованием языка многомерной геометрии. Работа с ним будет способствовать формированию навыков взаимодействия специалистов различного профиля при выполнении междисциплинарных научных проектов.


ISBN 5-85213-301-9  Луцык В.И., 2000

 Бурятский госуниверситет, 2000


ВВЕДЕНИЕ

Ограничимся изобарными условиями (P=const) и будем понимать под фазовой диаграммой (ФД) упорядоченную совокупность линий, поверхностей и гиперповерхностей, располагающихся в n-мерной T-Z призме с основанием Z в виде (n-1)-мерного симплекса (не касаясь при этом ФД так называемых взаимных систем, у которых в основании призмы лежит выпуклый комплекс) и ортогональной ему осью температур и разделяющих различные гомогенные (однофазные) и гетерогенные (многофазные) состояния n-компонентных составов. Без таких диаграмм нельзя решить большинство задач материаловедения, геологии, химической технологии, металлургии.

Существует большое многообразие топологических типов ФД. В некоторых их них число многомерных геометрических образов катастрофически увеличивается с повышением компонентности системы. Для их адекватного восприятия требуется определенный стиль мышления. Поэтому, например, металлурга определяют как специалиста, «думающего на языке фазовых диаграмм»[1]. Выработать подобные навыки мышления непросто. В старое время для этого использовали различные трехмерные макеты ФД или их проекций и разрезов (из проволоки, стекла, ниток, пластилина...), теперь стали общедоступными возможности машинной графики.

В данном пособии обобщается опыт разработки компьютерных технологий для синтеза изображений многомерных ФД и анализа их двух- и трехмерных проекций и разрезов. Предполагается, что оно облегчит взаимодействие специалистов разного профиля. Математикам и программистам будет полезна геометрическая постановка задачи, а «пользователям» диаграмм - принципы поиска оптимальных решений при разработке объектно-ориентированных программ на основе базовых алгоритмов и библиотеки объектов. Терминология теории гетерогенных систем и геометрической термодинамики используется в тексте в минимальном объеме, позволяющем перейти к обсуждению проблемы на языке многомерной геометрии.

Первая часть пособия “Конструирование многокомпонентных систем” посвящена высокосимметричной ФД из 25-ти поверхностей внутри треугольной призмы. Рассматриваемая во второй части пособия четырехмерная ФД такого же топологического типа состоит из 71-й гиперповерхности.

3

1. ГЕТЕРОГЕННЫЕ СИСТЕМЫ

Наряду с декартовыми будем применять подчиняющиеся нормировке z₁+z₂+...+z_n=1 и имеющие физический смысл в пределах n-вершинного симплекса Z барицентрические координаты, чтобы строить ортогонально им Т-Z диаграмму.

1. 
   Фазовые равновесия на ребрах симплекса.
   

На каждое ребро симплекса проецируется какой-либо тип ФД двойной системы (рис.1). Для обозначений верхних, промежуточных и нижних линий ФД, а в системах большей мерности – (гипер)поверхностей, введем символы q, s, v. Они соответствуют названию границ фазовых областей (liquidus, solidus, solvus), а их очередность в алфавите согласуется с положением линий относительно оси Т: T_q>T_s>T_v. Ниже каждой бинарной диаграммы показан принцип кодирования линии по ее Z-проекции.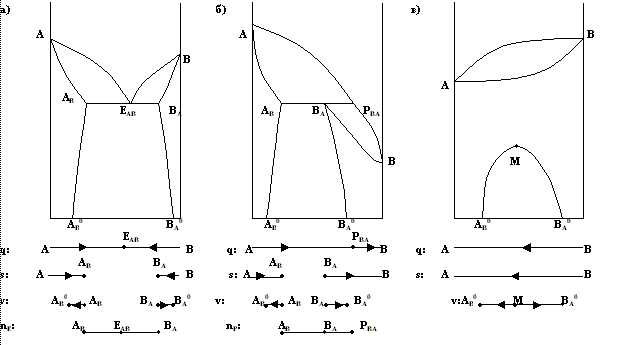



Рис. 1. Кодирование линий бинарных ФД на Z-проекциях

Выше линий q располагается гомогенная жидкость (liquid). В твердом состоянии (solidтвердый) компоненты A и B содержат примесь (В и A, соответственно). Зависимость ее количества от температуры характеризуют линии s и v. Чтобы обратить внимание на наличие твердофазной растворимости (solveрастворять), гомогенные твердые

фазы обозначают буквами греческого алфавита (Aa, Bb, С, D).
Если для эвтектической системы (рис. 1,а) обозначения A-B и B-A

идентичны, то вследствие ассиметричности перитектической ФД

4

(рис.1,б) записи A-B (p_AB или A_p-B) и B-A (p_BA или B_p-A) обозначают различные ФД: с T_A>T_B и с T_B>T_A. Линии s_A, s_B; v_A, v_B эвтектической, и линии v_A, v_B перитектической ФД можно считать трансформированными ветвями кривых s и v в системе с непрерывными рядами твердых растворов ab (рис. 1,в).

Горизонтальные отрезки n_EI_JJ_Is_E=I_JE_IJ+J_IE_IJ и n_pI_JP_IJ)= =(I_JJ_Is_р)+J_IP_IJ соответствуют нонвариантным (nonvariant) равновесиям. Весь отрезок n_Es_E называют солидусом, так как ниже его нет жидкой фазы. У отрезка n_p «солидусный» только сегмент A_BB_As_P, а ниже B_Ap_BA в двухфазной области L+b есть и расплав. Отрезки n_E, n_p и их сегменты иногда рассматривают в качестве совместившихся верхних и нижних границ выродившейся в прямую линию области L+a+b. В тройной системе каждый из них становится образующим элементом линейчатой поверхности.

Ни о каком сосуществовании трех фаз в бинарной изобарной системе не может быть и речи, хотя оно подразумевается в неудачном выражении «нонвариантное равновесие». Неудачном потому, что любое фазовое равновесие с ненулевой вариантностью (со степенями свободы) предполагает реальное сосуществование этих фаз, а любое химическое равновесие – равенство скоростей прямой и обратной реакций. Здесь же вместо слов «сосуществование» и «равновесие» уместнее понятие «аннигиляция», ибо речь действительно идет об исчезновении (поглощении) одной из фаз из-за невозможности реально обеспечить с высокой точностью заданное правилом фаз Ф+С=К+1 постоянство и давления, и температуры.

1.2. Моделирование нелинейчатых и линейчатых (гипер)поверхностей.

С повышением компонентности системы увеличивается мерность каждого геометрического образа ФД. Так, линии q, s и v (рис. 1,а) становятся в Т-х-у диаграмме нелинейчатыми поверхностями (рис. 2, табл. 1) с такой же кодировкой.

Если на ограняющих многокомпонентную систему (МКС) бинарных ФД есть горизонтальные отрезки, то внутри ФД МКС они трансформируются в линейчатые (гипер)поверхности. Аналогично, гори зонтальные плоскости Т-х-у диаграмм и горизонтальные тетраэдры Т--х-у-z диаграмм (а также их двух- и трехмерные сегменты) становятся образующими элементами для четырех- и пятимерных линейчатых

гиперповерхностей четверных и пятерных T-Z диаграмм.

5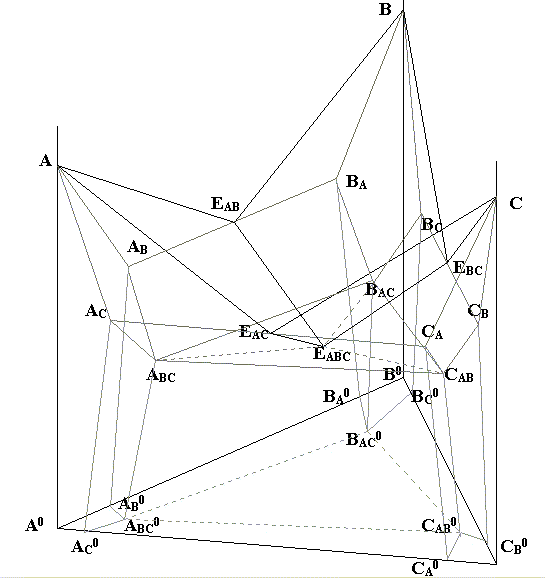

Рис. 2. Триметрическая проекция диаграммы

эвтектического типа (E^eee)

Для аппроксимации нелинейчатых (гипер)поверхностей можно предложить большой спектр уравнений. Для линейчатых – такой выбор пока что ограничен уравнением трехмерной косой плоскости [2].

Таблица 1.

Строение поверхностей диаграммы

эвтектического (Е^еее) типа (рис.2-3)
6

Поверхности (к-во)	Контур	Образующие	Направляющие
qI (3)	IEIJEIKEABC	-	-
sI (3)	IIJIKIJK	-	-
sE (1)	АВСВАССАВ	-	-
vIJ(3) [и vJI(3)]	IJIJKIJK0IJ0	-	-
qIJr(3) [и qJIr(3)]	IJEIJEABCIJK	IJEIJ(IJKEABC)	IJIJK, EIJEABC
sKr (3)	IJJIIJKJIK	IJJI(IJKJIK)	IJIJK, JIJIK
vKr (3)	IJK0IJKJIKJIK0	IJKJIK(IJK0JIK0)	IJKIJK0, JIKJIK0

В наших задачах можно обойтись и без уравнений линейчатых (гипер)поверхностей, если определять координаты вершин образующего симплекса (в тройной системе - отрезка) при заданной температуре и значение функции отклика для заданной на симплексе Z точки из совместного решения уравнений, описывающих направляющие (линии, поверхности, гиперповерхности) и образующий (отрезок, треугольник, тетраэдр и т.д.) геометрические элементы.

1.3. Особенности диаграмм с 25-ю поверхностями (рис. 2-3).

Если на гранях призмы взять диаграммы из 7-ми линий (такие, как на рис. 1,а или 1,б), то внутри ее расположатся 1 горизонтальная плоскость при температуре пересечения верхних q_I поверхностей, 12 нелинейчатых (3q_I+3s_I+6v_IJ) и 12 линейчатых (6q_IJ^r+3s_I^r+3v_I^r) поверхностей. Кроме ориентации в пространстве и физической природы поверхностей, символы q^r, s^r, v^r характеризуют и их линейчатый (ruled) характер. Ограничимся эвтектическим типом (рис. 1,а) всех ограняющих систем I-J и расположением точки E_ABC пересечения трех поверхностей q_I и горизонтальной плоскости n_E ниже всех E_IJ на гранях призмы, который допускает аддитивную аппроксимацию нелинейчатых поверхностей (рис. 2). Обозначим такой тип диаграммы символом Е^еее, т.е.: три бинарные эвтектики находятся выше тройной эвтектики.

Существует большое многообразие таких диаграмм из 25 поверхностей: Е^еер, Q^ep_e, P^e_pp и т.д. Они отличаются различным сочетанием бинарных систем I-J, I_P-J и J_P-I (рис.1, а,б), а также положением тройной точки (E, Q или P) пересечения поверхностей q_I и формой соответствующей горизонтальной плоскости n_E, n_Q или n_P. Ниже всех трех бинарных точек (E_IJ или p_IJ) находится точка E, ниже двух из них располагается квазиперитектическая точка Q, а ниже одной – перитектическая точка P. Принадлежащие плоскости нонвариантного «равновесия» (n_E, n_Q или n_P) вершины L(E,Q,P), A_BC, B_AC, C_AB образуют дву-

7

мерные четырехвершинные комплексы: с точкой Е внутри симплекса А_ВСВ_АСС_АВ(рис. 2), внешней точкой Q у выпуклого четырехугольника QА_ВСВ_АСС_АВ и точкой I_JK внутри симплекса PJ_IKK_IJ. Как и в случае бинарной системы, вся плоскость n_E – солидусная. У плоскостей n_Q и n_P солидусные только сегменты А_ВСВ_АСС_АВ. Горизонтальные плоскости и их сегменты тоже часто трактуются как верхние и нижние границы выродившейся области L+a+b+.

2. НЕЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ q_I, s_I, v_IJ

Важной особенностью в расположении 12-ти нелинейчатых поверхностей q_I, s_I, v_IJ являются их пересечения в 4-х точках: в Е_АВС пересекаются три поверхности q_I, а в трех точках I_JK – одна s_I c двумя v_IJ и v_IK. Причем, все эти точки имеют одну и ту же температурную координату и принадлежат горизонтальной плоскости s_Е. В качестве исходных данных будем пользоваться только координатами особых точек бинарных систем I-J (табл. 2).

Таблица 2.

Параметры (T; массовая доля I) диаграмм I-J (рис. 1,а; 2)

I	I-J	IJ0	IJ	EIJ	JI	JI0	J
1000;1	A-B	20;0.82	650;0.76	650;0.45	650;0.21	20;0.08	800;0
1000;1	A-C	20;0.80	450;0.77	450;0.4	450;0.27	20;0.10	600;0
800;1	B-C	20;0.93	450;0.65	450;0.45	450;0.26	20;0.11	600;0

2.1. Верхние q_I (рис. 3,а).

Выразим уравнение каждой поверхности q_I через принадлежащие ей точки I, E_IJ, E_IK. Найдем пересечение E_ABC (табл. 3) трех плоскостей q_I и соединим с E_IJ.

Алгоритм (нахождение координат пересечения плоскостей q_I)

Начало

M [1][1] = koefA(A, E_AB, E_AC);

M [1][2] = koefB(A, E_AB, E_AC);

M [1][3] = koefC(A, E_AB, E_AC);

N [1] = - koefD(A, E_AB, E_AC);

{ плоскость AE_ABE_AC  q_A}

M [2][1] = koefA(B, E_AB, E_BC);

M [2][2] = koefB(B, E_AB, E_BC);

M [2][3] = koefC(B, E_AB, E_BC);

N [2] = - koefD(B, E_AB, E_BC);

{ плоскость BE_ABE_BC  q_B }

M [3][1] = koefA(C, E_BC, E_AC);

8

M [3][2] = koefB(C, E_BC, E_AC);

M [3][3] = koefC(C, E_BC, E_AC);

N [3] = - koefD(C, E_BC, E_AC);

{ плоскость CE_BCE_AC  q_C } {рассчитаны коэффициенты А, В, С, D нормальных уравнений плоскостей q_A, q_B, q_C}

{решая систему этих трех уравнений, получаем Е_ABC}

D[0]=opr3(M);

Для LU1=1 по 3 цикл

Для LU2=1 по 3 цикл

Для LU3=1 по 3 цикл MA[LU2][LU3] = M[LU2][LU3];

КонецЦикла; КонецЦикла;

Для LU2=1 по 3 цикл MA[LU2][LU1] = N[LU2]; КонецЦикла;

D[LU1] = opr3(MA); КонецЦикла;

Для LU1=1 по 3 цикл EABC[LU1] = D[LU1]/D[0];

КонецЦикла; Конец;

Примечания