Луцык В.И. Конструирование многокомпонентных систем. В. И. Луцык конструирование многокомпонентных систем. I. Txy диаграммы с 25ю поверхностями учебнометодическое пособие
 Скачать 1.53 Mb. Скачать 1.53 Mb.
|
а)Детали алгоритмаФункции koefA(), koefB(), koefC(), koefD(), opr3() вычисляют соответственно коэффициенты А, В, С в нормальном уравнении плоскости Ax+By+Cz+D=0 и значение определителя третьего порядка. Функция opr3(M[3][3]) Возврат opr3 = M[1][1](M[2][2]M[3][3] - M[2][3]M[3][2]) - - [1][2](M[2][1]M[3][3] - M[3][1]M[2][3]) + + [1][3](M[2][1]M[3][2] - M[2][2]M[3][1]); КонецФункции; Функция koef(A[3][3], В[3][3], С[3][3]) Возврат koefА = (В[2]-А[2])(В[3]-А[3]) - (С[2]-А[2])(С[3]-А[3]); Возврат koefВ =-((В[1]-А[1])(В[3]-А[3]) - (С[1]-А[1])(С[3]-А[3])); Возврат koefС = (В[1]-А[1])(С[2]-А[1]) - (С[1]-А[1])(В[2]-А[2]); Возврат koefD = А[1]koefА + A[2]koefВ + A[3]koefС; КонецФункции; б) Математический аппарат Случай 1 (с преобразованием координат Z в декартовы XY). Плоскость АEАВEАС задает уравнение   X - XA Y - YA T - TA X - XA Y - YA T - TA XEAB - XA YEAB-YA TEAB-TA = 0 (*), XEAС - XA YEAС -YA TEAС -TA 9 где A(Z1A,Z2A,Z3A,TA) A(1,0,0,TA), XEAB=XAZ1EAB+XBZ2EAB+XCZ3EAB, YEAB=YAZ1EAB+YBZ2EAB+YCZ3EAB. Ему соответствует определитель: (X-XA)((YEAB-YA)(TEAС-TA) - (YEAС-YA)(TEAB-TA)) - - (Y-YA)((XEAB-XA)(TEAС-TA) - (XEAС-XA)(TEAB-TA)) + + (T-TA)((XEAB-XA)(YEAС-YA) - (XEAС-XA)(YEAB-YA)) = = KX+LY+MT+P=0, где Р = -КXA-LYA-MTA (1) Приведя уравнения плоскостей ВEАВEВС, СEАСEВС к виду (1), 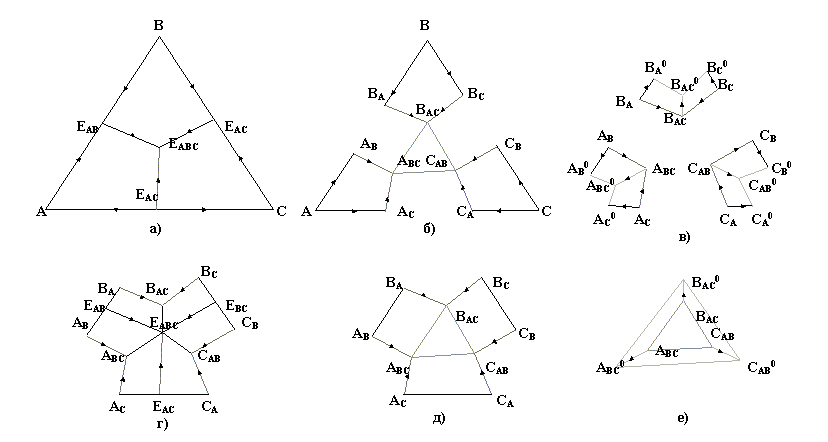 Рис. 3. Z–проекции нелинейчатых (а-в) и линейчатых (г-е) поверхностей системы Ееее решаем систему трех уравнений: K1X + L1Y + M1T + P = 0 K2X + L2Y + M2T + P = 0 K3X + L3Y + M3T + P = 0 Х+(L1/K1)Y+(M1/K1)T+P1/K1=0; Y+(M4/K4)T+P4/K4=0; (M5/L5-M4/L4)T+(P5/L5-P4/L4)=0; T=-(P5/L5-P4/L4)/(M5/L5-M4/L4), где L4=L2/K2-L1/K1; L5=L3/K3-L1/K1; M4=M2/K2-M1/K1; M5=M3/K3-M1/K1; P4=P2/K2-P1/K1; P5=P3/K3-P1/K1. Получив значение Т, определяем Y, а затем и X. Случай 2 (без преобразований координат). Начинается с (*). 2.2. Промежуточные sI и sE (рис. 3,б). Выразим уравнения плоскостей sI через координаты точек I, IJ, IK. Решив каждое из них совместно с уравнением горизонтальной плоско 10 сти при ТЕABC, найдем пересечения полученных линий уровня ТЕABC с гранями призмы (точки IEJ, IEK). За координаты точки IJK (табл. 3) примем середину полученного отрезка IEJIEK (вариант 1) или пересечение линии одного уровня с лучом IEABC (вариант 2), или же произвольно выбранную точку на линии уровня. Соединим точки IJK между собой (плоскость sE) и с IJ, JI (плоскости sI). Алгоритм {Вариант 1: Для sA отрезок AECAEB делим пополам (точка АBC), причем точки AEC и АЕВ ищем как пересечение плоскости T=TE и горизонтальных прямых ААС и ААВ. Вариант 2: Для sA точку АBC дает пересечение прямых AEАВС и AECAEB} {алгоритм нахождения точки пересечения трех плоскостей} …Если Вариант1 = ИСТИНА Тогда Для i=1 по 3 цикл АBC[i] = (AEB[i] + AEC[i])/2; КонецЦикла; ИначеЕсли Вариант2 = ИСТИНА Тогда {нахождение точки пересечения двух прямых} {tg1=(xAEВ-xAEС)/(yAEВ-yAEС), tg2=(xE-xA)/(yE-yA)} ABC[1]=(xA-xAEС+yAEСtg1-yAtg2)/(tg1-tg2) ABC[2]=tg2(xA-xAEС+yAEСtg1-yAtg1)/(tg1-tg2)+xA ABC[3]=TE Конец; Таблица 3. Координаты тройных точек в системе Ееее
2.3. Нижние vIJ, vIK (рис. 3,в). По заданным координатам точек IJ, IJ0 и IK, IK0 на гранях призмы и полученным в 2.2 координатам их общей с sI и sE точкой IJK внутри призмы, рассчитываем уравнения плоскостей vIJ, vIK при каждой вершине I. Решая их совместно с горизонтальной плоскостью Т=Т0 в основании призмы, находим точки IJK0. Алгоритм {определяем точку АBC0 } … {алгоритм нахождения точки пересечения трех плоскостей} 3. ЛИНЕЙЧАТЫЕ ПОВЕРХНОСТИ 3.1. Верхние qIJr, qJIr (с горизонтальными образующими 11 IJEIJ(IJKEABC) и JIEIJ(JIKEABC)) (рис. 3,г). Воспользуемся координатами точек IJ, EIJ при ТЕIJ и IJK, EABC при ТЕABC. Для каждой из шести линейчатых поверхностей через две пары точек зададим уравнения двух прямых, которым принадлежат направляющие отрезки IJIJK и EIJEABC. Найдем зависимость координат сопряженных точек (на образующих отрезках) от температуры. Алгоритм {для поверхности qABr с образующими ABEAB(ABCEABC), К – количество пар сопряженных точек} начало dTM=(EAB[3]–EABC[3])/K; dTN=(AB[3]–ABC[3])/K; Для i=1 по K-1 цикл TM[i]=EABC[3]+i*dTM; TN[i]=ABC[3]+i*dTN; MX[i]=((EAB[1]–EABC[1])(TM[i]–EABC[3]))/(EAB[3]–EABC[3])+EABC[1]; MY[i]=((EAB[2]–EABC[2])(TM[i]–EABC[3]))/(EAB[3]–EABC[3])+EABC[2]; NX[i]=((AB[1]–ABC[1])(TN[i]–ABC[3]))/(AB[3]–ABC[3])+ABC[1]; NY[i]=((AB[2]–ABC[2])(TN[i]–ABC[3]))/(AB[3]–ABC[3])+ABC[2]; КонецЦикла …{ аналогично для остальных поверхностей} Конец; Математический аппарат {для EАВЕABC} (X-XEABC)/(XEAB-XEABC)=(Y-YEABC)(YEAB-YEABC)=(T-TEABC)(TEAB-TEABC), тогда X =(XEAB-XEABC)(T-TEABC)/(TEAB-TEABC)+XEABC и Y=(YEAB-YEABC)(T-TEABC)/(TEAB-TEABC)+YEABC , где Т пробегает T=ТEАВ-ТЕABC с неким шагом. 3.2. Промежуточные sKr (с образующими IJJI(IJKJIK)) (рис. 3,д). Аналогично 3.1. Уравнения прямых, которым принадлежат направляющие отрезки, задаем через точки IJ, IJK и JI, JIK. 3.3. Нижние vKr (с образующими IJKJIK(IJK0JIK0)) (рис. 3,е). Аналогично 3.1. и 3.2. Направляющие отрезки IJKIJK0 и JIKJIK0. 4. ФАЗОВЫЕ ОБЛАСТИ ДИАГРАММЫ Ееее (рис. 4, табл. 4) Нелинейчатые и линейчатые поверхности и грани призмы формируют трехмерные фазовые области: одну Ł, одну a+b+g и по три Ł+i, Ł+i+j, i, i+j. В рассматриваемом температурном интервале область Ł имеет только боковые (грани призмы) и нижние (поверхности qI) гра 12 ницы. Каждая область i ограничена тремя гранями призмы (две боковые и нижняя), поверхностью sI и двумя поверхностями vIJ, vIK (рис. 4,а). Область i+j формируют боковая и нижняя грани призмы, нелинейчатые поверхности vIJ, vJI и линейчатые sKr, vKr. (рис. 4,г). Область a+b+g опирается на основание призмы, а сверху и сбоку ограничена плоскостью sE и тремя поверхностями vKr(рис. 4,д). Таблица 4 Границы фазовых областей системы Ееее
У области Ł+i сверху - поверхность qI, снизу - sI, qIJr, qIKr, сбоку - две боковые грани призмы (рис. 4,б). Область Ł+i+j задают горизонтальный сегмент IJKJIKEABC плоскости sE и три линейчатые поверхности, образованные отрезком IJJI и его сегментами IJEIJ, JIEIJ: нижняя sKr и верхние qIJr, qJIr (рис. 4,в). На рис. 4 нет виртуальной области Ł+a+b+g, выродившейся в плоскость sEºABCBACCAB, но в табл. 4 перечислены три ее верхние границы EАВСIJKJIK и нижняя – вся плос кость sE, а на рис. 5,д показан и “изотермический разрез”. Для визуализации горизонтальных (изотермических) разрезов фазовых областей при T=Tизот соединяем точки на пересечениях контуров нелинейчатых поверхностей на границах одно- и двухфазных областей и стыкуем с ними образующие отрезки линейчатых поверхностей на границах двух- и трехфазных областей. Так, при TB>Tизот>TC (считаем ТEАВ>ТEАС=ТEВС, ТА>ТВ>ТС) попарно соединяются точки с T=Tизот на контурах нижних границ qА и qВ области L: U1 c U2 и U3 с U4 (рис. 5,а). На вертикальных (политермических) разрезах следы от пересечения нелинейчатых поверхностей отображаются 13 аналогично, а следы линейчатых поверхностей либо совпадают с образующим отрезком, либо получают аддитивные искажения (если не проходят через рассчитанные с заданным шагом точки). 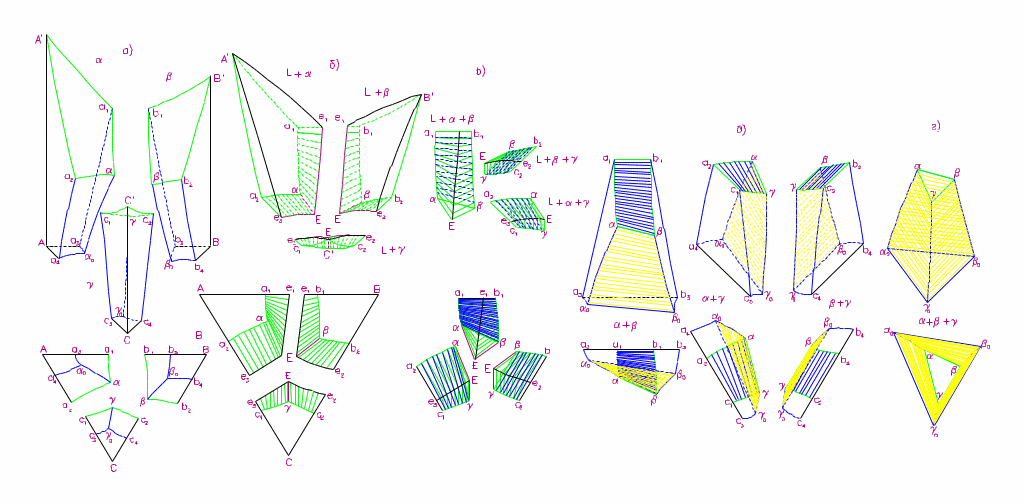 Рис. 4. Фазовые области системы Ееее и их Z-проекции (символы точек отличаются от обозначений на других рисунках) Рис. 4. Фазовые области системы Ееее и их Z-проекции (символы точек отличаются от обозначений на других рисунках)При проецировании фазовых областей или образующих их поверхностей на основание призмы области i+j, Ł+i+j и a+b+g разбиваются на термодинамически неустойчивые фрагменты, отличающиеся очередностью выделения кристаллов при охлаждении расплава Ł. 5. РАЗРЕЗЫ ФАЗОВОЙ ДИАГРАММЫ Ееее 5.1. Горизонтальные разрезы (рис. 5). Известны координаты точек, задающих все нелинейчатые и линейчатые поверхности. Для визуализации горизонтальных разрезов нелинейчатых поверхностей надо знать, пересекаются ли их контуры с плоскостью Т=Тизот; то есть, лежит ли Т=Тизот между максимальной и минимальной температурой каждой поверхности. Если да, то ищем эти точки (для каждой поверхности их не более 2-х) и соединяем отрезком. Так, на контуре AEABEACEABC (ТEАВС<Тизот z2=((Tизот-ТEAB)/(ТEABC-ТEAB))(z2(EABC)-z2(EAB))+z2(EAB), z3=((Tизот-ТEAB)/(ТEABC-ТEAB))(z3(EABC)-z3(EAB))+z3(EAB). Для линейчатых поверхностей те же формулы дают при Т=Тизот 14 : 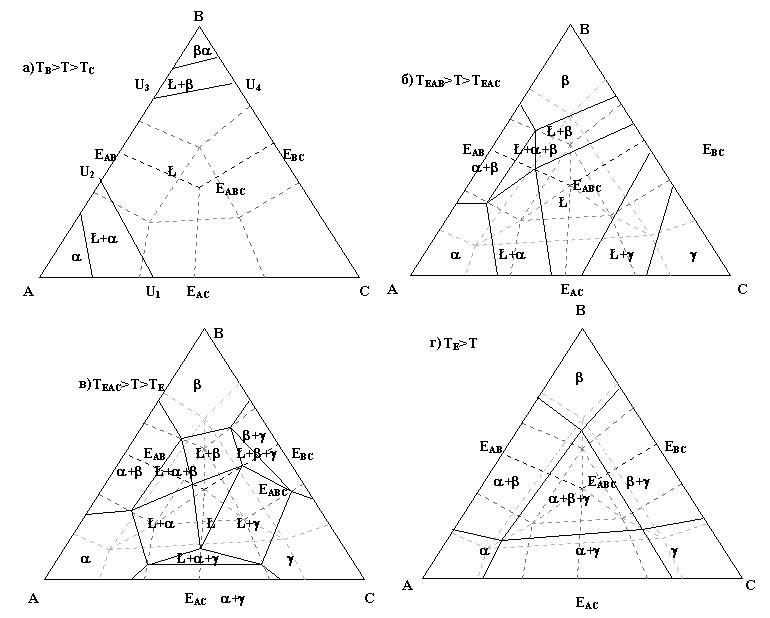 Рис. 5. Горизонтальные разрезы Т-Z диаграммы Ееее концы образующих отрезков на направляющих. Так, для qАВr zi=((Tизот-ТEAB)/(ТEABC-ТEAB))(zi(EABC)-zi(AB)+zi(AB). Алгоритм {Вначале идет перебор комбинаций:} k=0 Если T<=Tmax и T>=Tmin тогда Если T<=Tmax и T>=Tм тогда k=k+1 От i=1 до 4 цикл zk[i]=(T-Tм)(zL[i]-zM[i])/(Tmax-Tм)+zM[i] конец цикла конец если Если T<=Tmax и T>=Tk тогда k=k+1 От i=1 до 4 цикл zk[i]=(T-Tk)(zL[i]-zk[i])/(Tmax-Tk)+zk[i] конец цикла конец если ... конец если {Построение надписей:} … Если (Т1 15 всех точек, задающих фазовую область} X10=SX1j/n;{cуммирование по j} X20=SX2j/n; Вывод(X10, X20 , «L»); КонецЕсли … 5.2. Вертикальные разрезы (рис. 6). По координатам точек, задающих все поверхности визуализируется и вертикальный разрез ФД. Аналогично 5.1., надо перебрать все возможные сочетания вершин контура каждой поверхности, определяя, какая из таких "комбинаций" пересекается плоскостью разреза, задаваемой точками P1, P2 на симплексе Z и точкой с проекцией на отрезке P1P2, но имеющей отличную от него температуру. При этом каждый раз решаем систему уравнений, задающих отрезок контура и вертикальную плоскость. Затем определяем, лежит ли найденная точка между двумя исходными: 0£(zi-ziAb)/(ziAbc-ziAb)£1. Чтобы устранить искажение, поворачиваем плоскость разреза до совпадения с плоскостью экрана (f - угол между ними, x=cosf, y=sinf) Все найденные точки строим ортогонально P1P2. Алгоритм.'>Алгоритм. Вертикальный разрез строится аналогично горизонтальному. 6. ФАЗОВЫЕ РЕАКЦИИ И ЗАВИСИМОСТЬ СОСТАВА ФАЗ ОТ ТЕМПЕРАТУРЫ Пересечение перпендикуляром к симплексу Z любой поверхности соответствует окончанию предыдущей и началу последующей фазовой реакции. Надо записать всю цепочку таких реакций и отобразить изменение составов участвующих в них фаз. В случае аддитивной модели ФД состав расплава при достижении плоскости qI в точке G (рис. 7) ‘‘уходит’’ по ней от вершины I симплекса Z, одноименной с выпадающими первичными кристаллами i’, т.е. по лучу IG. Состав кристаллов меняется вдоль этого же луча по плоскости sI от точки G’ при TG до точки H’G. Составы кристаллов, попадающих в двухфазную область i+j сначала соответствуют концам образующего отрезка линейчатой поверхности sKr, проходящего через точку G, а затем движутся прямолинейно по плоскостям vIJ, vJI таким образом, что при любой температуре их соединяют горизонтальные отрезки, совпадающие в проекции с образующей. В трехфазных областях путь изменения фаз задают линии пересечения поверхностей qI+qJ, sI+vIJ и vIJ+vIK. Симплекс Z разбивается при проецировании на него поверхностей и фазовых областей на 33 двумерных концентрационных поля (рис. 7). Принадлежность любого состава одному из полей дает подстановка его координат в уравнения границ полей и сравнение полученного результата со знаками контрольных точек. Только 6 полям отвечают 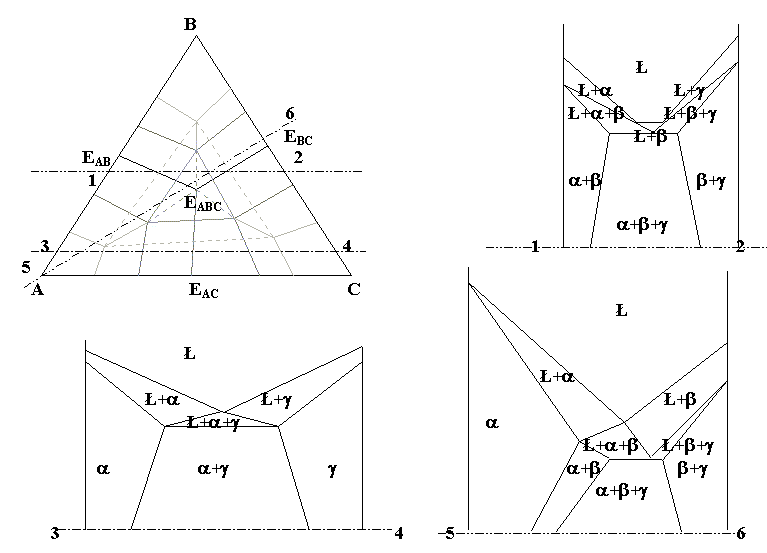 Рис. 6. Топология вертикальных разрезов Т-Z диаграммы системы Ееее (кривизна линейчатых поверхностей не учтена) уникальные цепочки фазовых реакций: II: ŁàŁ’+i’ài’(3 поля); IIJ: ŁàŁ’+i’àŁ’’+i’+ie+jeài’+i’’+j’’(6 полей); IIIJ: ŁàŁ’+i’ài’ài’+i’’+j’’(6 полей); IIJK: ŁàŁ’+i’àŁ’’+i’+ie+jeài’+i’’+j’’ài’+i’’+j’’+k’’(6); IIIJK: ŁàŁ’+i’àŁ’’+i’+ie+jeàŁE+i’+iE+jE+kEài’+i’’+j’’+k’’(6); IIIIJK: ŁàŁ’+i’ài’ài’+i’’+j’’ài’+i’’+j’’+k’’(6 полей). ; На контурах полей (на линиях и в точках, то ли имеющих реальный физический смысл, то ли соответствующих формальному пересечению линий) схемы фазовых реакций отличаются: EAB1: ŁàŁ’’+ae+beàa’’+b’’; 12: ŁàŁ’’+ae+beàa’’+b’’àa’’+b’’+g’’; 2EABC: ŁàŁ’’+ae+beàŁ’’’+a’’+b’’àŁE+aE+bE+gEàa’’+b’’+g’’; EAC3: ŁàŁ’’+ae+geàa’’+g’’; 34: ŁàŁ’’+ae+geàa’’+g’’àa’’+b’’+g’’; 4EABC: ŁàŁ’’+ae+geàŁ’’’+a’’+g’’àŁE+aE+bE+gEàa’’+b’’+g’’; EBC5: ŁàŁ’’+be+geàb’’+g’’; 17 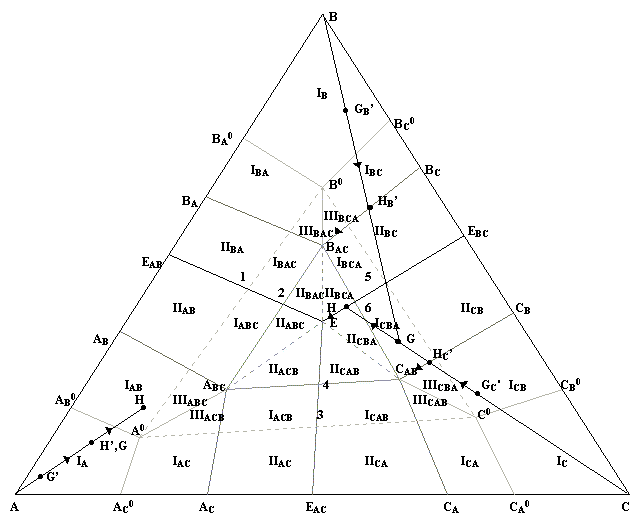 Рис. 7. Концентрационные поля и схемы кристаллизации 56: ŁàŁ’’+be+geàb’’+g’’àa’’+b’’+g’’; 6EABC: ŁàŁ’’+be+geàŁ’’’+b’’+g’’àŁE+aE+bE+gEàa’’+b’’+g’’; ABCABC0: ŁàŁ’+a’àa’àa’+a’’+b’’+g’’; BACBAC0: ŁàŁ’+b’àb’àb’+a’’+b’’+g’’; CABCAB0: ŁàŁ’+g’àg’àg’+a’’+b’’+g’’; ABCEABC: ŁàŁ’+a’àŁE+aE+bE+gEàa’’+b’’+g’’; BACEABC: ŁàŁ’+b’àŁE+aE+bE+gEàa’’+b’’+g’’; CABEABC: ŁàŁ’+g’àŁE+aE+bE+gEàa’’+b’’+g’’; EABC: ŁàŁE+aE+bE+gEàa’’+b’’+g’’. Изменения составов равновесных фаз визуализируются: в поле IA путь кристаллизации состоит из линии GH на qA и линии G’H’ на sA (H’G); в поле ICBA составы расплава и первичных кристаллов сначала меняются по лучу CG, пока не пересекут соответственно EBCEABC в H и CBCAB в H’, затем спуск идет по HEABC и H’CAB. Алгоритм {Проверка принадлежности полю} Если G принадлежит AEABEACEABC тогда Начало Если G принадлежит AB0ABC0ABCEABCEAB тогда 18 {Проверка принадлежности полям IAB, IIAB, IABC, IIABC, IIIABC} Если G принадлежит AС0ABC0ABCEABCEAС тогда {Проверка принадлежности полям IAС, IIAС, IACB, IIAСB IIIAСB} {проводится следующим способом} {Проверка принадлежности точки G(z1,z2,z3) полю IA} Если z3>0 и z2>0 тогда Если (z2-z2Ab0)(z3Abc0-z3Ab0)-(z3-z3Ab0)(z2Abc0-z2Ab0)<0 тогда Если (z2-z2Ac0)(z3Abc0-z3Ac0)-(z3-z3Ac0)(z2Abc0-z2Ac0)<0 тогда {Принадлежит полю} Конец … 7. БАЛАНС МАСС СОСУЩЕСТВУЮЩИХ ФАЗ И КРИСТАЛЛОВ РАЗЛИЧНОГО ПРОИХОЖДЕНИЯ Для заданных состав и температуры точки G рассчитываются массовые доли равновесных фаз (с учетом вклада кристаллов различного происхождения) как в конце кристаллизации, так и в любой момент одного из ее этапов. Определим фазовую область, в которую попадают продукты кристаллизации исходного расплава G при заданной температуре и построим схему всех предшествующих этапов кристаллизации: а) Для двухфазной области: LàSI’(рис. 8,а). При TH£Tj£TG ищем точку P на IG при T=Tj,где H -точка пересечения IG с EIJEABC или EIKEABC, G’- так называемая сопряженная G точка, лежащая на sI при Т=TG, P’ сопряженная P точка на IG’ при T=Tj, тогда L(Tj)=GP’/PP’ и SI‘(Tj)=GP/PP’; б) Для трехфазной области: LàSI’’+SJ’’(рис. 8,б). При TEABC£Tj£TH ищем точку Q на EIJH при T=Tj (где QI’ сопряженная Q точка на IjQ при T=Tj, а QJ’ сопряженная Q точка на JjQ при T=Tj). Ищем точку X являющуюся пересечением QG с QI’QJ’, тогда Ł(Tj)=GX/QX, SI’(Tj)+SI’’(Tj)+SJ’’(Tj)=QG/QX и (SI’+SI’’)/SJ’’=zIX/zJX; в) Для двухфазной области: SI’àSJ’’(рис. 8,в). Существует конодный отрезок GIGJ, на котором лежит точка G. Точки GI,GJ находятся из уравнений линий VIWI, VJWJ и уравнения пропорциональности GIVI/WIVI=GJVJ/WJVJ. Тогда SI(Tj)=GGI/GIGJ; SJ(Tj)=GGJ/GJGI; г) Для трехфазной области: SI’àSJ’’+SK’’(рис. 8,г). Существует конодный треугольник YIYJYK(YI принадлежит IJKIJK0 и т.д.), при температуре которого лежит точка G. Точки RI, RJ, RK являются пересечением отрезков YKYJ с IJKG, YIYK с JIKG и YIYJ с KIJG соответственно. Тогда SI(Tj)=GRI/RIIJK; SJ(Tj)=GRJ/RJJIK; SK(Tj)= 19 =GRK/RKKIJ. Алгоритм … Если G лежит в AEABEACEABC тогда Если TH£Tj£TG тогда Начало L(Tj)=GP’/PP’ S’A(Tj)=GP/PP’ Конец Если TEABC£Tj£TH тогда {Расчет баланса масс для трехфазной области} … 8. ВОССТАНОВЛЕНИЕ ЭЛЕМЕНТОВ ФД ПО РАЗРЕЗАМ 8.1. Восстановление координат тройной эвтектики. Даны 2 вертикальных разреза 1-2, 3-4 (рис. 9). Поскольку точки Qi принадлежат образующим qr, расположенным на sE, то точку ЕABC даст пересечение прямых Q1Q3 и Q2Q4. Алгоритм {алгоритм нахождения точки пересечения двух прямых} 8.2. Восстановление конод. Построить коноду по 2 вертикальным разрезам и принадлежащей ей точке G.  Рис. 8. Схемы расчета баланса масс Рис. 8. Схемы расчета баланса масс20 Имеются 2 вертикальных разреза. На одном из них известна принадлежащая коноде точка G. На искомую точку G’ накладываются условия: 1)TG=TG’; 2) (xG’-x3)/(x4-x3)=(yG’-y3)/(y4-y3) – G’ принадлежит второму разрезу; 3) (xG’-xG)/(xI-xG)=(yG’-yG)/(yI-yG) – G’ принадлежит прямой IG. Они определяют систему уравнений, решением которой и являются координаты точки G’. Алгоритм {основывается на предыдущих алгоритмах} 9. ИССЛЕДОВАНИЕ АДДИТИВНЫХ МОДЕЛЕЙ ТОПОЛОГИЧЕСКИХ АНАЛОГОВ ФД Ееее 9.1. Зависимость тройной точки от температуры двойных. В уравнении A1x+B1y+С1T+D1=0 проходящей через точки I, eIJ, eIK плоскости A1=(yeIJ-yI)(TeIK-TI)-(yeIK-yI)(TeIJ-TI), B1=(TeIJ-TI)(xeIK-xI)-(TeIK-TI)(xeIJ-xI), C1=(xeIJ-xI)(yeIK-yI)-(xeIK-xI)(yeIJ-yI), D1=-xI((yeIJ-yI)(TeIK-TI)-  Рис. 9. Вертикальные разрезы для восстановления ЕАВС -(yeIK-yI)(TeIJ-TI))-yI((TeIJ-TI)(xeIK-xI)-(TeIK-TI)(xeIJ-xI))-TI((xeIJ-xI)(yeIK-yI)-(xeIK-xI)(yeIJ-yI)), причем A1, B1 и D1 линейно зависят от TeIJ и TeIK. Рассмотрим точку E как решение системы линейных уравнений для IeIJeIK, JeIJeJK, KeIKeJK. Из соотношений  21 следует, что при изменении температуры одной бинарной эвтектики eIJ изменятся коэффициенты A1,B1,D1 и A2,B2,D2. Так как они линейно зависят от TeIJ, то xE, yE и TE являются кубическими функциями от TeIJ. Изменение двух бинарных точек eIJ, eIK дополнительно меняет и A3,B3,D3, причем A1,B1,D1 являются линейными функциями двух переменных TeIJ,TeIK. В этом случае зависимость xE или yE от TeIJ и TeIK третьей степени, а TE от TeIJ и TeIK - четвертой. При изменении температур трех эвтектик коэффициенты A1,B1,D1; A2,B2,D2 и A3,B3,D3 линейны соответственно от TeIJ,TeIK; TeIJ,TeJK, и TeIK,TeJK. Зависимость xE или yE от TeIJ , TeIK , TeJK третьей степени, а TE от TeIJ , TeIK и TeJK - четвертой. 9.2. Топологические аналоги тройных систем эвтектического типа с различным расположением нонвариантных точек. 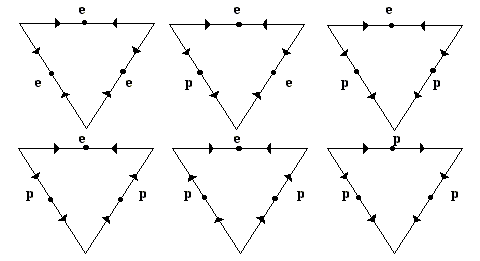 Рис. 10. Типы ФД, задаваемые бинарными (е, р) точками Помимо различия по типу тройной точки (E,Q,P) и заданной ею горизонтальной плоскости, Т-х-у диаграммы с 25 поверхностями отличаются характером взаимодействия в бинарных системах (рис. 10). Для каждого такого внешнего периметра у трех пересекающихся поверхностей qI возможно существование не более семи различных подтипов систем: один – с тройной точкой Е и по три - с Q и P(за счет ассиметричности линии ликвидуса относительно одной из бинарных систем). Исключив из их числа диаграммы с винтовым характером внешнего периметра, получим 24 подтипа систем (рис. 11), из которых 22 только всего 8 (Eeee, Qep>e, Qep> , Pep> , Ep> , Q e, Q , P p> ), могут быть построены с помощью аддитивной модели.: e e e e  |
