Луцык В.И. Конструирование многокомпонентных систем. В. И. Луцык конструирование многокомпонентных систем. I. Txy диаграммы с 25ю поверхностями учебнометодическое пособие
 Скачать 1.53 Mb.
|
|
а) декартовы координаты Для плоскости 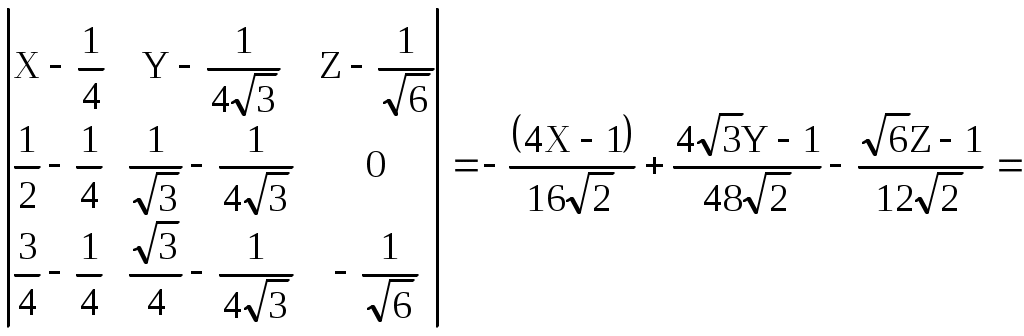 : 32 Р 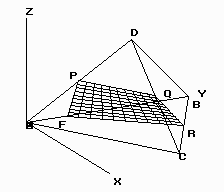 ис. 16. Плоскость (слева) и косая плоскость (справа) в тетраэдре . Аналогичное выражение получим и для плоскостей PRS, QRS, PQS (преобразуемое в тождество при подстановке координат четвертой точки плоскости PQRS). б) барицентрические координаты После раскрытия четырех определителей для плоскостей PQR, PSR, QRSи PQS получаем одинаковые коэффициенты в уравнении единой плоскости PQRS, преобразуемом в тождество при подстановке координат недостающей точки: 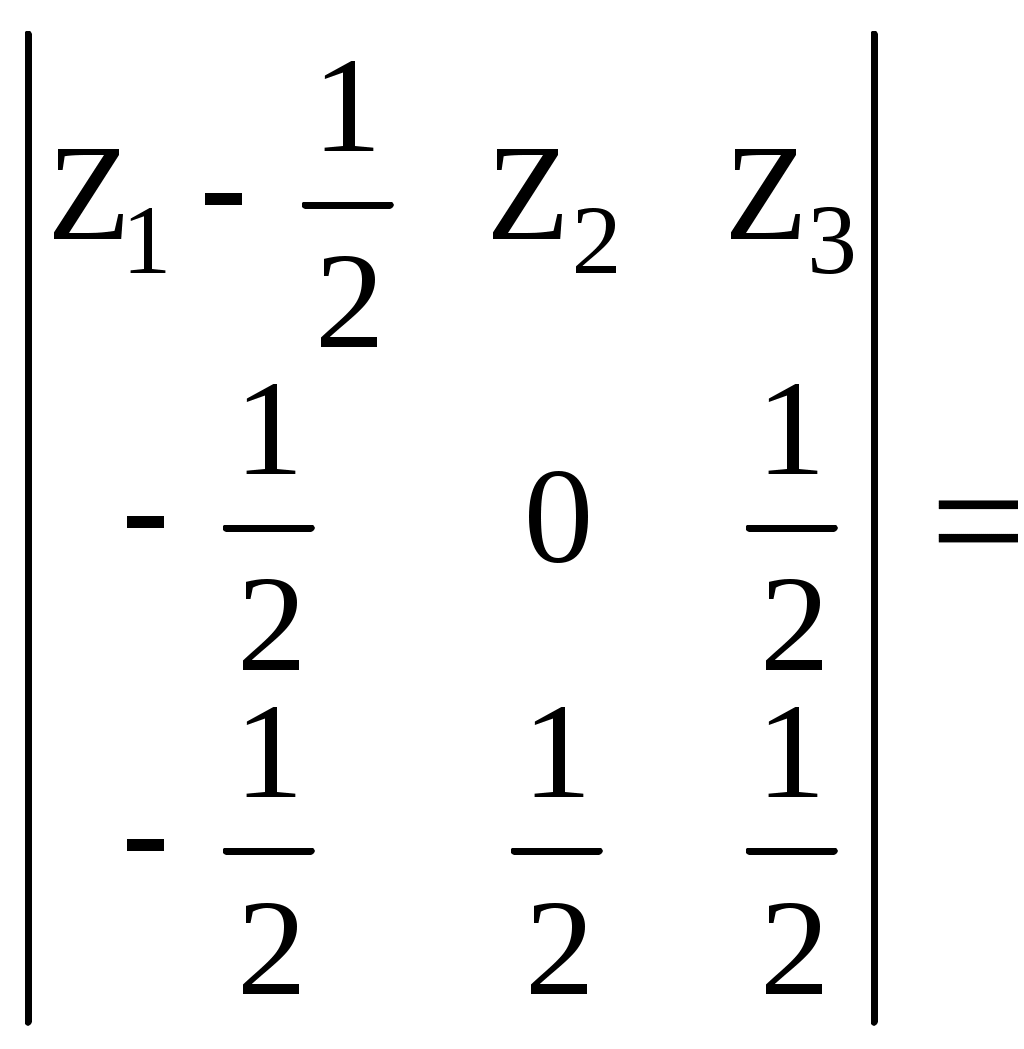 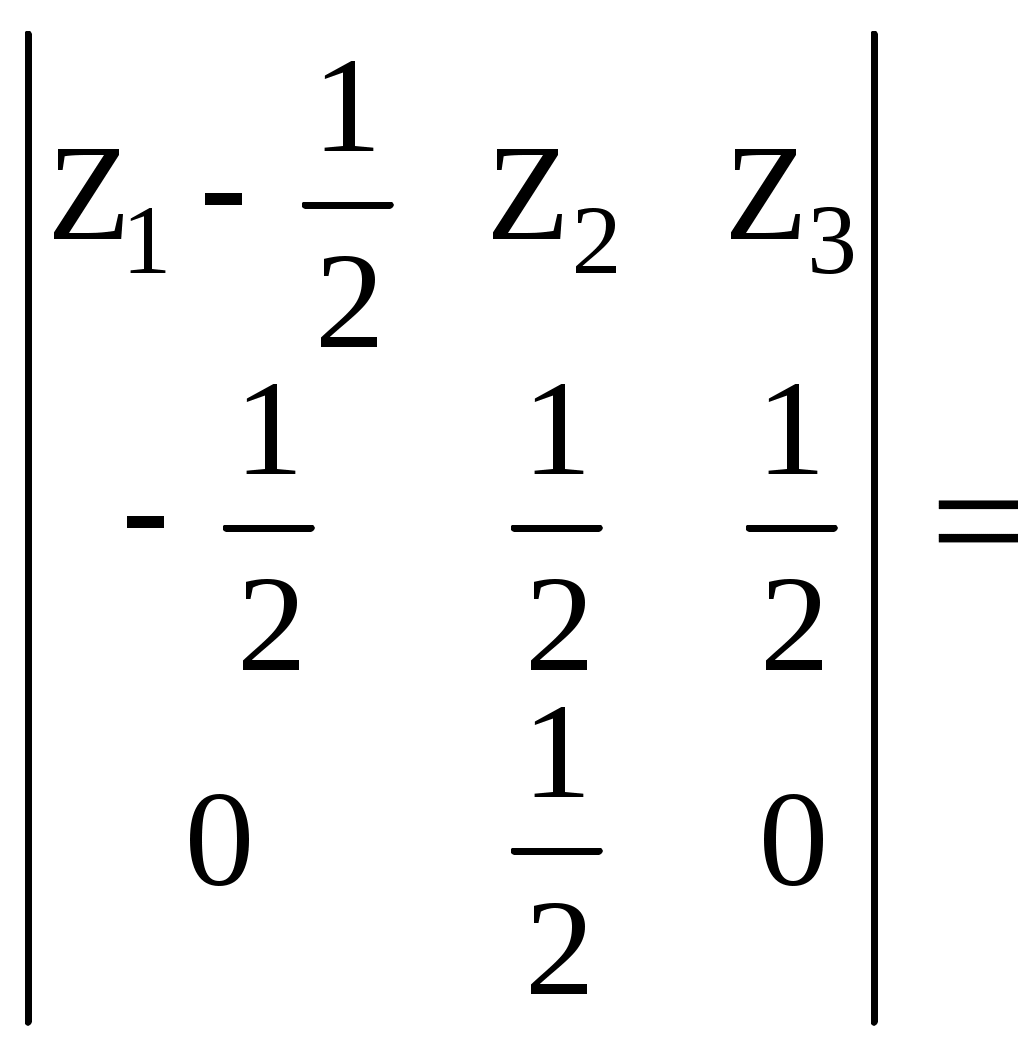 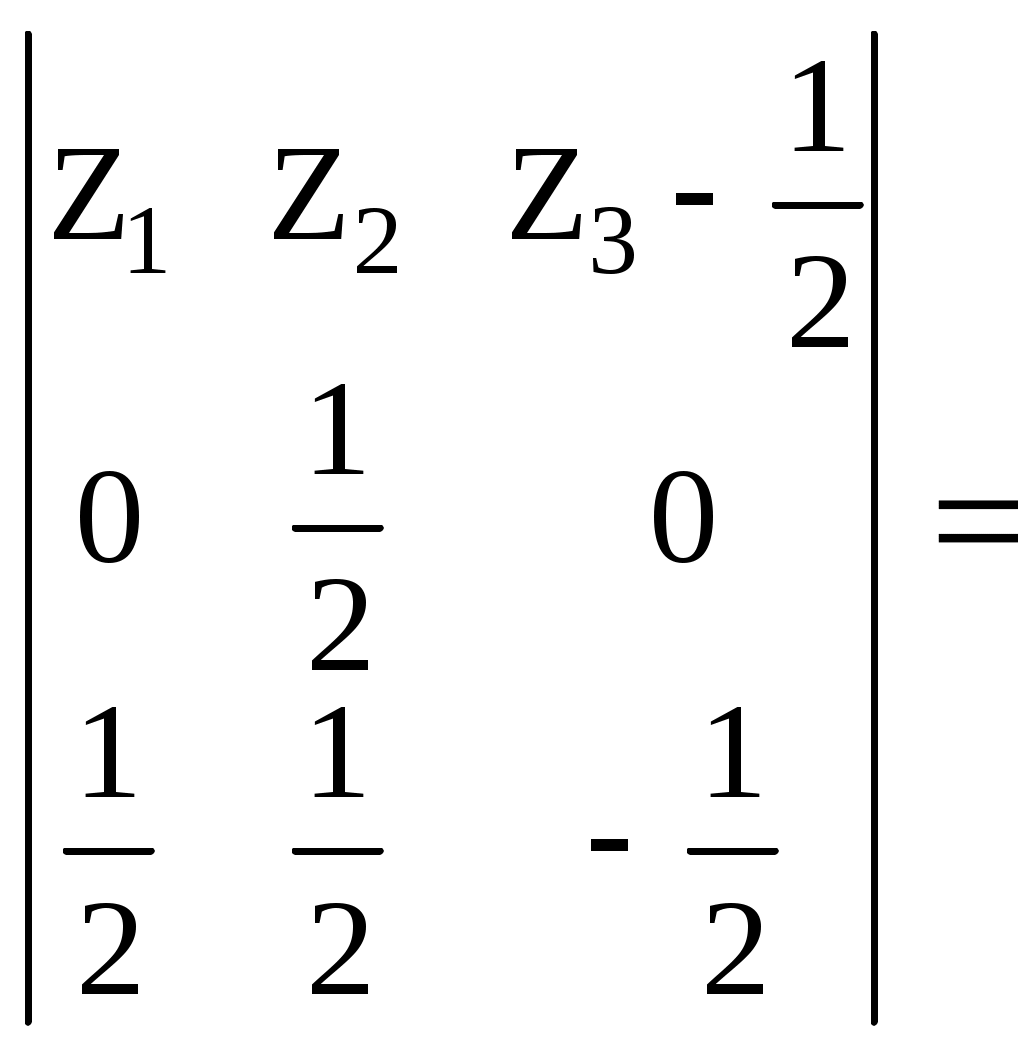 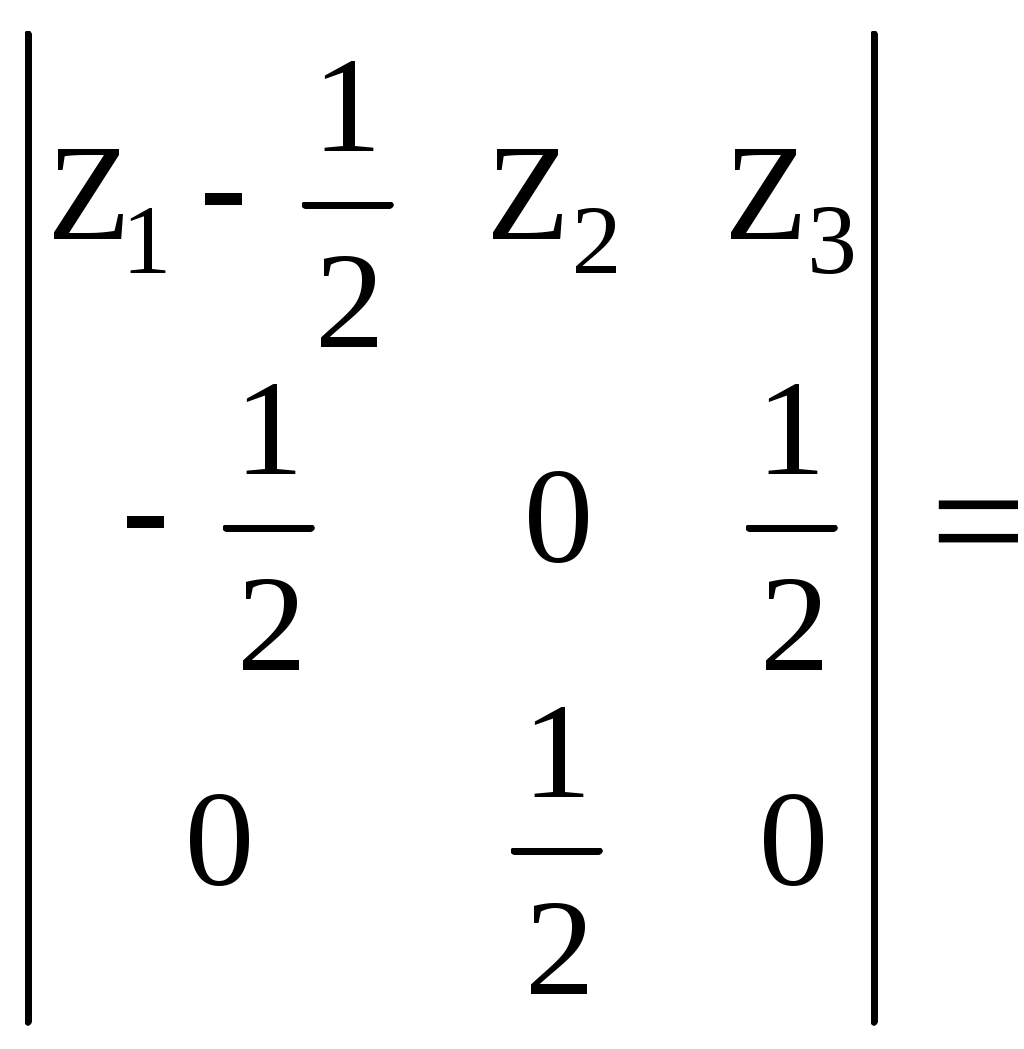 =2Z1+2Z3-1=0. Учитывая z1+z2+z3+z4=1, получаем еще одно эквивалентное выражение единого уравнения плоскости:  . Из чего следует, что рассматриваемая плоскость параллельна ребрам АС и ВD.10.1.2. Вывод нормального уравнения плоскости через произвольное положение образующего ее отрезка (инженерный способ). Пусть плоскость PQRS есть линейчатая поверхность, у которой  , - образующие, а  , - направляющие.  и  - концевые точки бегущего образующего отрезка  , де33 лящие направляющие 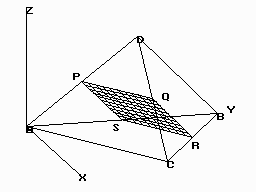и в отношении   , справедливом для любой проекции точек P, S, M и Q, R, N, а, следовательно, для любой их координаты (декартовой, барицентрической,…). Поэтому любую координату U точек M и N можно выразить через соответствующую координату U для точек P, S и Q, R. Например,  , откуда  .Если подставить в уравнение отрезка MN зависимости для каждой из координат точек М и N, то полученное уравнение будет выражать положение образующего отрезка при любом значении  . Следовательно это и будет уравнение всей линейчатой поверхности, а в данном случае - плоскости PQRS. Рассмотрим его вывод подробнее для заданных декартовых и барицентрических координат точек P, Q, R, S.a) декартовы координаты Подставим  ,  ,  ,  ,  ;  (табл. 1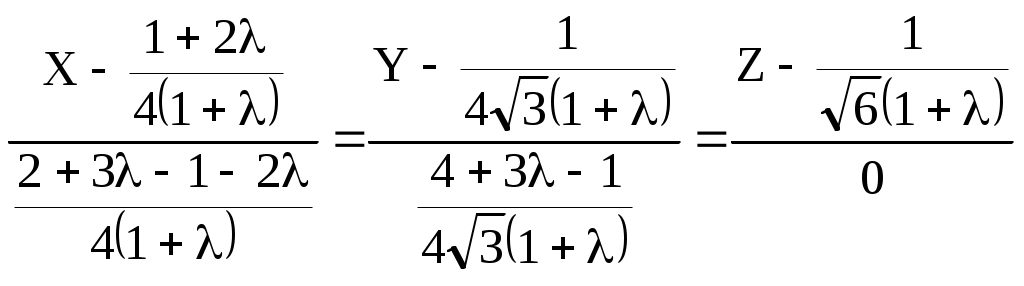) в уравнение образующей MN:  . Тогда  . Т.к. обращение в нуль одного из знаменателей означает и обращение в нуль числителя, то  . Преобразуем два первых члена :  34или  Получаем всё то же уравнение плоскости PQRS:  Повлияет ли на вид уравнения взаимная замена образующих и направляющих? Рассмотрим образующий отрезок M’N’, где M’QP и 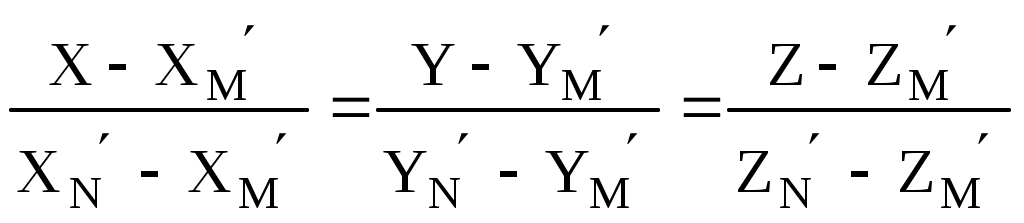 :  ,  ,  ,  ,  ,  ,   Поскольку в этом случае нет возможности выразить 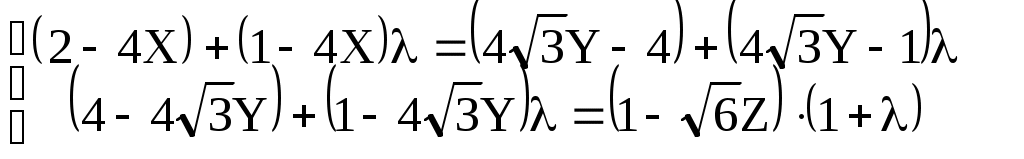 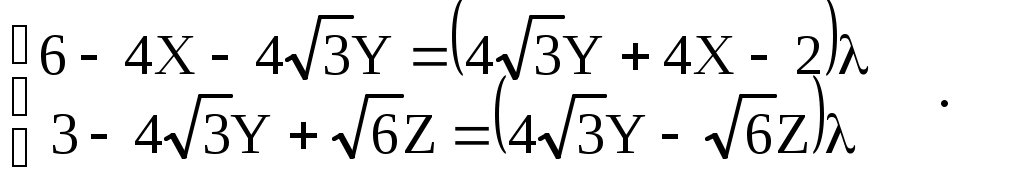проще, представим все выражение как систему двух уравнений, приравняв первую дробь ко второй и к третьей:  Откуда:  , а из равенства двух дробей в последнем выражении, получим в очередной раз всё то же уравнение плоскости PQRS:  .б) барицентрические координаты   Оставим в уравнении MN первую и третью дроби: Z1 - 0.5 = - Z3,35 откуда  . Это уравнение плоскости PQRS. Есть еще одна возможность получить его, но уже в эквивалентном виде, из выражения для числителей второй и четвертой дробей:  или  . Аналогичный результат получим и для образующего отрезка M’N’. 10.2. Косая плоскость. Проведем аналогичные рассуждения для косой плоскости PQRF (рис. 17, табл. 6). Получим уравнения второй степени в декартовых и барицентрических координатах:  ,20z42 + 8z1z4 - 4z1 - 8z4 - 33 = 0. 10.3. Некоторые свойства косой плоскости. На примере косой плоскости, вписанной в куб, удобно показать ее плоскости параллелизма. Пусть косая плоскость (рис. 17, справа) производна от плоскости B1D1H1F (рис. 17, слева) с уравнением в декартовых и барицентрических координатах: 1-2Х=0 и z1-z3=0. Таблица 5. Координаты вершин куба ABCDEFGH и заданной точками на его ребрах косой плоскости (рис.17) :
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
