дидактические материалы. Дидактические материалы по МПМ в нач. кл.. В. Н. Медведская Дидактические материалы по методике преподавания математики в начальных классах

• Название: В. Н. Медведская Дидактические материалы по методике преподавания математики в начальных классах
• Анкор: дидактические материалы
• Дата: 08.06.2020
• Размер: 1.28 Mb.
• Имя файла: Дидактические материалы по МПМ в нач. кл..doc
• Тип: Документы; #128875
• страница: 4 из 12

Б в раз М в раз

в) обобщение и формулирование правил

II ОЗНАКОМЛЕНИЕ СО СПОСОБОМ РЕШЕНИЯ

Выбор арифметического действия Запись Счёт

решения Ответ

Вычисление

III. ФОРМИРОВАНИЕ УМЕНИЯ решать задачи конкретного типа

Достаточно много. Рассредоточенно. Приём сравнения. Творческие задания.

3адания к схеме №10

1. 
   Перечислите типы задач (6 типов), входящих в данную группу.
   
2. 
   Охарактеризуйте содержание подготовительной работы к введению задач на увеличение числа в несколько раз.
   

3. Какие знания и умения учащиеся должны приобрести на этапе подготовки к решению задач на уменьшение числа в несколько раз, на кратное сравнение чисел?

4. С какой целью учитель предлагает практические упражнения вида: "Положите 2 круга, а ниже положите квадраты: 3 раза по 2 квадрата." Какие вопросы следует затем задать классу? Будет ли учитель в данной ситуации использовать метод сообщения новых знаний?

5. 
   Составьте алгоритм для практического способа решения задачи: "Имеется 6 квадратов. Кругов надо взять в 3 раза меньше. Сколько кругов надо взять?"
   
6. 
   Объясните смысл записи Б в □ М в □.
   
7. 
   Переформулируйте вопрос задачи на кратное сравнение чисел так, чтобы стало очевидно, что для ответа на этот вопрос нужно выполнять деление.
   

8. К каким обобщениям следует подвести детей в результате выполнения достаточного количества практических работ, аналогичных приведенным в схеме? Сформулируйте три соответствующих правила.

9. Прочитайте разными способами выражения 2·3, 6:3.

10. 
    Какие требования к наглядной интерпретации задачи должны быть выполнены, если цель вашей работы — "открыть" арифметический способ решения задач данного типа?
    

11. В каких ситуациях полезно, решив задачу арифметическим способом, предложить учащимся решить эту же задачу практическим способом?

12. Доказательство правильности выбора арифметического действия может быть: а) экспериментальным (на основе непосредственного восприятия практических действий с предметами или на основе представления об этих действиях), б) логическим (рассуждения на основе теоретических знаний: понятия, правила). Какому из этих двух способов доказательства вы отдадите предпочтение на уроках ознакомления с задачами в косвенной форме? Почему?

13. Назовите пары типов задач, которые целесообразно предлагать учащимся для сравнения на этапе формирования умения решать задачи из данной группы.

14. Какие дидактические функции выполняют задачи на увеличение (уменьшение) числа в несколько раз в косвенной форме?

15. Предложите творческие задания, способствующие формированию умения решать задачи на уменьшение числа в несколько раз.

СХЕМА № 11

МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ ПРОСТЫХ ЗАДАЧ НА НАХОЖДЕНИЕ НЕИЗВЕСТНЫХ

КОМПОНЕНТОВ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ
I. ПОДГОТОВИТЕЛЬНАЯ РАБОТА
а) решение задач на нахождение суммы и остатка;

б) усвоение названий компонентов и результатов арифметических действий (12 терминов);

в) знание правил нахождения неизвестных компонентов арифметических действий (8 правил).
II. ОЗНАКОМЛЕНИЕ СО СПОСОБОМ РЕШЕНИЯ

счёт

Выбор арифметического действия Запись решения Ответ

вычисление

а ) на сложение и вычитание — сюжетные б) на умножение и деление — с отвлечёнными числами

III. ФОРМИРОВАНИЕ УМЕНИЯ решать задачи конкретного типа

Достаточно много. Рассредоточенно. Приём сравнения. Творческие задания.

Задания к схеме №11

1. 
   Перечислите все типы задач, входящих в данную группу.
   
2. 
   Назовите этапы обучения решению задач на нахождение неизвестного уменьшаемого. Что можно утверждать о последовательности работы над другими типами задач данной группы?
   
3. 
   Охарактеризуйте содержание подготовительной работы к введению задач на нахождение неизвестного слагаемого (неизвестного делителя).
   
4. 
   Назовите 12 терминов и 8 правил, которые могут быть использованы при решении задач данной группы. Являются ли эти знания необходимыми?
   
5. 
   Чем объясняется, что в начальных классах задачи на нахождение неизвестных компонентов сложения и вычитания предлагаются сюжетные, а на нахождение неизвестных компонентов умножения и деления – с отвлеченными числами, т.е. с числами без наименований, взятыми не из описания какого-либо явления, события реальной действительности.
   
6. 
   Постройте графическую модель для задач на нахождение неизвестного вычитаемого. Оцените ее значимость для поиска решения задач данного типа. Опишите эту модель, используя термины «целое» и «часть».
   
7. 
   Постройте схематическую модель для задач на нахождение неизвестного уменьшаемого и дайте обоснование выбора сложения для ее решения.
   
8. 
   Назовите по три способа решения задач на нахождение неизвестного слагаемого, уменьшаемого, вычитаемого, которые могут быть использованы учащимися.
   
9. 
   Какие из этих способов применимы для решения задач на нахождение неизвестного множителя, делимого, делителя?
   
10. 
    Дайте обоснование выбора действия для решения задач на нахождение неизвестного делителя.
    
11. 
    Чем можно объяснить отсутствие практических работ учащихся на этапе подготовительной работы к решению задач данной группы?
    
12. 
    Почему задачи на нахождение неизвестного множителя, делимого и делителя в начальных классах решаются только алгебраическим способом?
    
13. 
    Дайте теоретико-множественное обоснование выбора арифметического действия для задач на нахождение неизвестного слагаемого, уменьшаемого, вычитаемого.
    
14. 
    Вы уже, конечно, обратили внимание, что на этапе формирования умения для любой группы типов задач используются одни и те же методические приемы. Дайте этому психолого-педагогическое обоснование.
    

СХЕМА №12

ИЗУЧЕНИЕ НУМЕРАЦИИ ЦЕЛЫХ НЕОТРИЦАТЕЛЬНЫХ ЧИСЕЛ


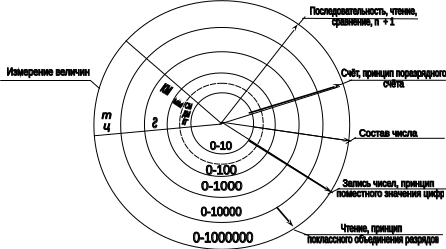
Задания к схеме №12

1. 
   О чем "говорят" концентрические круги на схеме?
   
2. 
   Какие концентры выделяются в учебниках белорусских авторов? Возможно ли выделение других концентров?
   

3. Что обозначают стрелки-радиусы? Назовите общие для всех концентров направления работы при изучении нумерации.

4. 
   Что на схеме обозначает запись п+1?Сформулируйте закодированный в ней принцип.
   
5. 
   Почему некоторые стрелки не выходят из общего центра кругов или имеют разную толщину? Какие направления работы в изучении нумерации они обозначают?
   
6. 
   Сформулируйте принцип поместного значения цифр и приведите конкретные примеры.
   
7. 
   Сформулируйте принцип поразрядного счета. Проиллюстрируйте его с помощью системы числовых равенств, а также с помощью различных моделей разрядных единиц.
   
8. 
   Сформулируйте принцип поклассного объединения разрядов. Какое отражение он находит в таблице разрядов и классов?
   

9. Почему знакомство с принципами поместного значения цифр и поразрядного счета начинается в теме "Двузначные числа"?

10. Помимо стрелок в концентрических кругах выделен общий сектор "Измерение величин". О какой особенности построения изучения нумерации он напоминает? Приведите конкретные примеры взаимосвязи нумерационных понятий и мер длины, массы.

11. Чем, по вашему мнению, объясняется введение I км и I г в концентре "Тысяча", а не в каком-либо другом?

12. Изучение каких величин может быть тесно связано с изучением нумерационных вопросов? Приведите конкретные примеры и дайте соответствующие обоснования. Верно ли аналогичное утверждение относительно такого раздела школьной программы, как "Время и его измерение"?

13. В процессе изучения чисел у учащихся постепенно расширяется представление о тех функциях, которые они могут выполнять. Назовите функции числа 9 в каждом из следующих математических описаний конкретной ситуации: 9 шаров, 9 см, 4•9, 9-й этаж.

14. Приведите несколько примеров, иллюстрирующих справедливость утверждения: "Знания по нумерации продолжают совершенствоваться при изучении арифметических действий".

15. Какие принципы позиционных систем удачно моделируются на счётах? На абаке? В таблице разрядов и классов?

СХЕМА № 13

ИЗУЧЕНИЕ СЛОЖЕНИЯ И ВЫЧИТАНИЯ В ПРЕДЕЛАХ ДЕСЯТКА

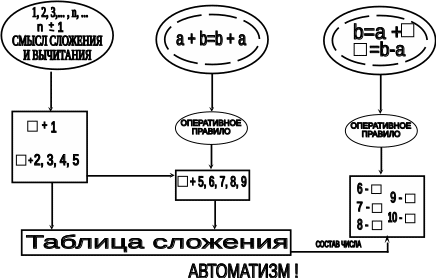
Задания к схеме №13

1. 
   При построении схемы использованы различные геометрические формы (овалы и прямоугольники), чтобы даже визуально подчеркнуть различие изучаемого материала по его характеру: теоретический (общее) и практический (частное). Сформулируйте обобщенные, теоретические знания, необходимые для осознанного применения и усвоения приемов сложения и вычитания чисел первого десятка: а) прибавления и вычитания по одному или по частям; б) перестановки слагаемых; в) вычитания на основе взаимосвязи вычитания со сложением.
   
2. 
   Какая из фигур (овал или прямоугольник) избранный: а) вопросы теории, б) практические вопросы данной темы?
   
3. 
   Почему каждый из овалов соединен стрелкой с каким-либо прямоугольником? Можно ли эту стрелку повернуть в противоположное направление? Что будет обозначать данная стрелка?
   
4. 
   Что обозначают стрелки, соединяющие прямоугольники? Можно ли их направить в противоположную сторону?
   
5. 
   Некоторые из вопросов арифметической теории уже в концентре "Десяток" доводятся до уровня обобщения, т.е. до формулировки и символической записи соответствующих правил, свойств, законов арифметических действий, а некоторые используются в практике вычислений неявно, т.е. на основе интуиции, здравого смысла и пока еще небольшого опыта детей. Какие из вопросов арифметической теории в первом классе применяются неявно? Как этот факт отражен в соответствующих овалах?
   
6. 
   Каким оперативным правилом, т.е. правилом, которое дети проговаривают и непосредственно применяют в практике вычислений, пользуются учащиеся при решении примеров вида 2+7 ?
   
7. 
   Правило нахождения неизвестного слагаемого (третий овал) также можно сформулировать в виде оперативного правила, используя для этого термины "целое" и "часть". Закончите его формулировку: "Если от целого отнять его часть, то ... "
   
8. 
   Назовите этапы работы по теме "Сложение и вычитание".
   
9. 
   Какой смысл имеет завершающее схему слово "Автоматизм"? Сформулируйте цель и задачи изучения темы "Сложение и вычитание в пределах десятка".
   
10. 
    Что включается в подготовительную работу к введению приемов: а) прибавления и вычитания числа по его частям; б) перестановки слагаемых; в) вычитания из чисел второго пятка?
    
11. 
    Объясните смысл термина «состав числа».
    
12. 
    С какой целью учитель предлагает систему заданий вида:
    

а) прочитать запись 5+3=8 слева направо и справа налево?

б ) дополнить записи числами 5+3= ; + =8; 5 + =8?

СХЕМА № 14

ИЗУЧЕНИЕ СЛОЖЕНИЯ И ВЫЧИТАНИЯ В ПРЕДЕЛАХ СОТНИ



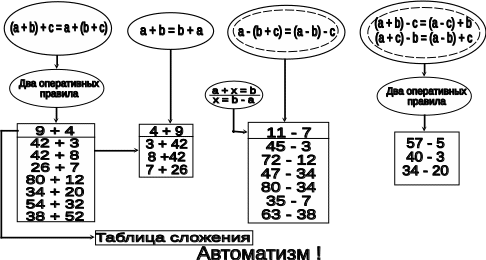
Задания к схеме №14

1. 
   Что обозначают овалы? Прямоугольники? Соединяющие их стрелки?
   
2. 
   Какие из вопросов арифметической теории в белорусских учебниках для первого класса вводятся в явном виде?
   
3. 
   Какие из вопросов арифметической теории используются неявно?
   
4. 
   Сформулируйте цель и задачи изучения темы "Сложение и вычитание в пределах 100".
   
5. 
   Термин "Автоматизм" в данной схеме относится как к табличному сложению и вычитанию, так и ко всем другим случаям, описанным в прямоугольниках. В чем же состоит различие в итогах работы над табличными и внетабличными случаями сложения и вычитания?
   
6. 
   Какие случаи сложения и вычитания в первом и в третьем прямоугольниках отделены от всех других?
   
7. 
   Почему стрелка к таблице сложения идет именно так, как изображено на схеме?
   
8. 
   Какое свойство сложения является теоретической основой приема прибавления числа по частям, в том числе и приема дополнения до десятка?
   
9. 
   Что является теоретической основой приема вычитания числа (однозначного или двузначного) по его частям?
   
10. 
    Какие другие приемы устного сложения и вычитания используются для двузначных чисел?
    
11. 
    Решите двумя способами каждый из следующих примеров:
    

13–8, 26+7, 45+23, 60–24.

12. 
    Почему третьему прямоугольнику соответствует два овала, а не один, как в других случаях?
    
13. 
    Как можно корректно на доступном детям языке сформулировать сочетательное и переместительное свойства сложения?
    
14. 
    Назовите этапы работы по теме "Сложение и вычитание в пределах сотни".
    
15. 
    Почему из всех прямоугольников стрелками соединены только первый и второй? Какую стрелку ещё можно провести? Почему?
    
16. 
    Сформулируйте по два оперативных правила для сложения и для вычитания, которыми будут оперировать учащиеся при решении удобным способом примеров из первого и из четвертого прямоугольников.
    
17. 
    Есть ли различия в работе по заучиванию таблиц сложения без перехода через десяток и с переходом через десяток?
    
18. 
    Как можно на уроке использовать калькулятор, чтобы мотивировать детей к запоминанию табличных результатов?
    

СХЕМА № 15

ИЗУЧЕНИЕ ПРИЁМОВ ПИСЬМЕННОГО СЛОЖЕНИЯ И ВЫЧИТАНИЯ


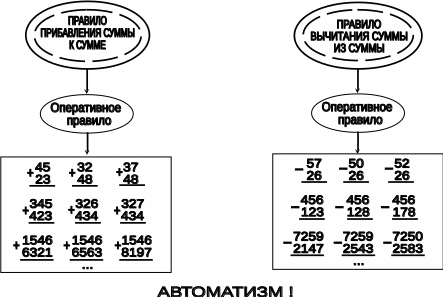
Задания к схеме №15

1. 
   Сформулируйте правила прибавления суммы к сумме и вычитания суммы из суммы. В качестве логических следствий из них выведите оперативные правила (в них находит отражение сущность приема поразрядного выполнения действий).
   
2. 
   Какие из этих четырех, сформулированных вами, правил используются в явном виде, а какие в неявном?
   

3. Назовите теоретическую основу для приема поразрядного сложения.

4. Почему вычитание можно тоже выполнять поразрядно? Есть ли другие приемы вычитания, например, двузначного числа из двузначного? Письменными или устными являются эти приемы?

5. Проанализируйте (по концентрам) цепочки примеров, записанные в первом прямоугольнике. Как в обучении письменному сложению реализуется принцип "от простого к сложному"?

6. 
   Действует ли этот принцип в обучении письменному вычитанию? Приведите соответствующие аргументы и примеры.
   
7. 
   Для концентра "Многозначные числа" составьте аналогичные цепочки примеров на сложение и примеров на вычитание.
   
8. 
   Какой из вариантов построения обучения письменному сложению и письменному вычитанию реализован в белорусских учебниках: последовательного или параллельного введения постепенно усложняющихся случаев сложения и вычитания?
   

9. Сформулируйте цель и задачи изучения приемов письменного сложения и вычитания. Что должно быть здесь доведено до уровня автоматизма?

10. Выполнение каких условий способствует формированию полноценных вычислительных навыков?

11. При переходе от одного концентра к другому для создания проблемной ситуации на уроках введения новых случаев письменного сложения или вычитания можно использовать методический прием "наращивания количества разрядов". Как в этом случае можно построить урок ознакомления со сложением трехзначных чисел? Четырехзначных? Многозначных?

12. Составьте несколько (по 2 – 3 для каждого из концентров) наиболее трудных для учащихся примеров на письменное вычитание.

13. Назовите два способа письменного сложения и письменного вычитания именованных чисел. Приведите соответствующие примеры.

СХЕМА № 16

ИЗУЧЕНИЕ ТАБЛИЧНОГО УМНОЖЕНИЯ И ДЕЛЕНИЯ



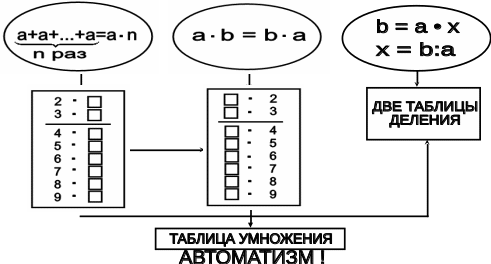
Задания к схеме №16

1. 
   Знание каких вопросов арифметической теории позволяет учащимся принимать непосредственное, активное участие в составлении таблиц умножения и деления?
   
2. 
   В явном или в неявном виде эти теоретические вопросы рассматриваются в начальном курсе математики?
   
3. 
   Сколько таблиц умножения по постоянному первому множителю зафиксировано в первом прямоугольнике? Какой основной способ нахождения произведений используется при их составлении?
   
4. 
   Можно ли некоторые из табличных произведений вычислять, не прибегая к замене умножения сложением одинаковых слагаемых? Приведите конкретные примеры.
   
5. 
   Назовите всевозможные способы нахождения табличных произведений.
   
6. 
   Почему второй прямоугольник соединен стрелками с овалом, изображающим переместительное свойство умножения, а также с первым прямоугольником?
   
7. 
   Сколько таблиц умножения по постоянному второму множителю зафиксировано во втором прямоугольнике? Нужно ли в этих случаях вычислять произведения? Приведите конкретные примеры.
   
8. 
   Изучение таблиц умножения с числами 2 и 3 дает числовой материал для наблюдения, сравнения и вывода по индукции переместительного свойства умножения. Как эта особенность отражена в первом и втором прямоугольниках?
   
9. 
   Какому из выражений 7∙3 или 3∙7 соответствует самая краткая форма их чтения: "Трижды 7"? Объясните, почему к сводной таблице умножения идет стрелка только от второго прямоугольника.
   
10. 
    С каким из прямоугольников соединен стрелкой последний прямоугольник? Чем вы это можете объяснить?
    
11. 
    Что является теоретической основой для составления таблиц деления? Нужны ли вычисления для нахождения частного в табличных случаях? Приведите несколько примеров из обеих таблиц деления.
    
12. 
    Какая из четырех таблиц, представленных в опорной схеме, является основной, исходной для всех других?
    
13. 
    Будут ли существенные различия в организации работы по запоминанию таблиц умножения (деления) и таблиц сложения (вычитания)?
    
14. 
    Какую роль может выполнить калькулятор в мотивации учащихся необходимости прочного запоминания таблиц?
    

СХЕМА № 17

ИЗУЧЕНИЕ ВНЕТАБЛИЧНОГО УМНОЖЕНИЯ И ДЕЛЕНИЯ В ПРЕДЕЛАХ СОТНИ



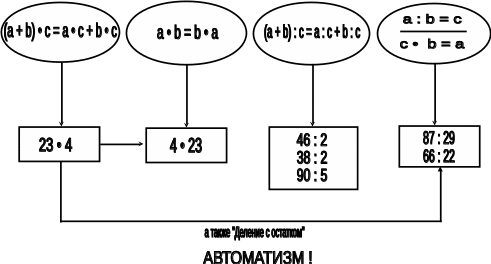
Задания к схеме №17

1. Какие законы умножения и деления в явном виде изучаются в данной теме?

2. Сформулируйте правило, отраженное в последнем овале. Где оно находит применение в начальном обучении математике?

3. Проанализируйте примеры, записанные в третьем прямоугольнике. Соответствует ли их последовательность принципу "от простого к сложному"? Какие отличия в способе их решения появляются при переходе от одного случая к другому?

4. Почему во всех других прямоугольниках отмечено по одному примеру?

5. Перечислите приемы вычислений, которые вводятся при изучении темы "Внетабличное умножение и деление". Назовите теоретическую основу для каждого из этих приемов.

6. Почему первый прямоугольник соединен стрелками со вторым и с четвертым прямоугольниками?

7. 
   Сформулируйте цель и задачи изучения темы "Внетабличное умножение и деление". Назовите этапы работы по данной теме и признаки их сходства.
   
8. 
   Что необходимо включать в подготовительную работу к введению способа подбора частного? Предложите несколько методических приемов, облегчающих детям подбор частного.
   

9. Дайте характеристику системы уроков по теме "Деление с остатком".

10. К чему в заданной схеме относится требование "Автоматизм!"?

11. В каких случаях умножения и деления в пределах ста формирование осознанности усвоения приема вычислений связано с использованием опоры (словесной модели вычислений) вида: "Заменю... Получился пример...Удобнее... ."? В белорусском учебнике "Математика 3" для этих способов вычислений найдите схематические модели.

12. Случаи вида 20 • 3, 80 : 2, 80 : 20 тоже относятся к внетабличным. Почему же они не включены в данную опорную схему?

13. В белорусском учебнике "Математика 3" помимо тех теоретических вопросов, которые уже отражены в опорной схеме, при изучении темы "Внетабличное умножение и деление" вводятся также правило деления числа на произведение и правило умножения числа на сумму. Найдите в этом учебнике соответствующие уроки и попытайтесь ответить на следующие вопросы: Где в данной теме применяются эти теоретические знания? Можно ли в концентре "Сотня" их вообще не рассматривать? Почему в концентре "Многозначные числа" эти (дополнительные) правила будут уже необходимы?

14. При изучении раздела "Умножение и деление" школьной программы очень четко просматривается принцип органического единства вопросов арифметической теории и практики вычислений. Проиллюстрируйте этот принцип на примере тем "Табличное умножение и деление" и "Внетабличное умножение и деление".

СХЕМА №18

ИЗУЧЕНИЕ УМНОЖЕНИЯ МНОГОЗНАЧНЫХ ЧИСЕЛ


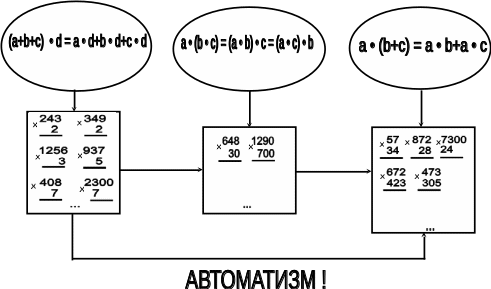
Задания к схеме №18

1. 
   Приобретают ли учащиеся при изучении темы "Письменное умножение" новые теоретические знания? Какие?
   
2. 
   Верно ли утверждение: "Знание учащимися правила умножения числа на произведение позволяет свести все случаи умножения на разрядные числа (т.е. на числа, оканчивающиеся нулями) к уже известным детям случаям умножения"? Как этот подход к введению новых приемов умножения отражен в опорной схеме? Находит ли он отражение в форме записи примеров вида 2300 • 7? 23 • 7000 ? 2300 • 7000 ?
   
3. 
   Что обозначают стрелки, соединяющие прямоугольники?
   
4. 
   Проанализируйте по рядам примеры, записанные в первом прямоугольнике, и охарактеризуйте, за счет чего идет усложнение условий применения алгоритма письменного умножения на однозначное число.
   
5. 
   Соблюдается ли этот подход при отработке умения умножать на разрядные числа? На двузначные и вообще на любые многозначные числа?
   
6. 
   К чему в данной опорной схеме относится требование "Автоматизм!"?
   
7. 
   Сформулируйте цель и задачи изучения темы "Письменное умножение".
   
8. 
   Назовите этапы работы по теме. Чем похожа работа на каждом из них?
   
9. 
   Почему отработке навыка применения алгоритма письменного умножения на однозначное число должно уделяться особенно много внимания?
   
10. 
    Какое практическое применение в теме "Письменное умножение" находят правила: умножения суммы на число, умножения числа на произведение, умножения числа на сумму?
    
11. 
    Охарактеризуйте содержание подготовительной работы к введению приема умножения на числа, оканчивающиеся нулями. Как вы определили, что обязательно следует включать в этап подготовки?
    
12. 
    При умножении именованного числа на отвлеченное, например, 23м 4см • 5, 23м 4см • 35, в алгоритм умножения включаются новые операции. Какие именно? Почему одна из них обязательно первая, а другая − последняя в этом новом алгоритме?
    
13. 
    Выполнение каких условий необходимо для совершенствования вычислительных навыков вообще и письменного умножения в частности?
    
14. 
    Каким образом принцип органической связи вопросов арифметической теории и практики вычислений отражен в заданной опорной схеме? В каких других опорных схемах он также очевиден?
    
15. 
    При переходе от одного концентра к другому на уроках введения новых случаев письменного умножения на однозначное число можно успешно использовать методический прием "наращивания количества разрядов". В чем вы усматриваете достоинства такого подхода к изложению нового материала? Можно ли этот же методический прием применить на других этапах изучения письменного умножения?
    

СХЕМА № 19

ИЗУЧЕНИЕ ПИСЬМЕННОГО ДЕЛЕНИЯ


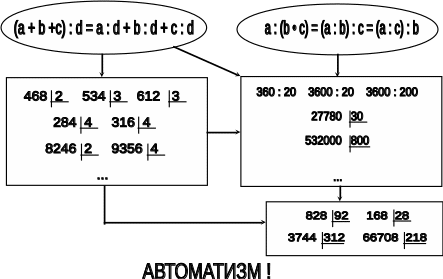
Задания к схеме №19

1. 
   По аналогии с заданиями для других схем по изучению арифметических действий самостоятельно сформулируйте вопросы к данной опорной схеме.
   
2. 
   Сравните все опорные схемы по изучению арифметических действий и сделайте несколько выводов об общности принципов построения обучения младших школьников устным и письменным вычислениям.
   
3. 
   Какое практическое применение в теме "Письменное деление" находят правила: деления суммы на число, деления числа на произведение.
   
4. 
   Выделите элементы нового на уроке ознакомления с алгоритмом письменного деления на однозначное число? Как в связи с этим можно подвести детей к новой форме записи деления?
   
5. 
   Почему отработке навыка применения алгоритма письменного деления на однозначное число следует уделять особенно много внимания?
   
6. 
   Какие новые операции включаются в алгоритм письменного деления на двузначное (многозначные) число? Предложите виды упражнений для отработки умения выполнять только эти новые операции.
   
7. 
   Какое место в системе изучения письменного деления занимают случаи деления с остатком?
   
8. 
   Каким способом выполняется деление значений величин, т.е. именованных чисел на отвлеченные числа? Какое место в системе обучения письменному делению занимают такие виды заданий?
   
9. 
   Объясните целесообразность такого построения изучения письменного умножения и письменного деления, когда сразу же после рассмотрения случая умножения на однозначное число (на разрядные числа, на двузначные и многозначные числа) вводится аналогичный случай деления.
   
10. 
    В каких случаях деления сначала находят пробные цифры частного, а потом окончательные? Почему их называют "пробные"? Проверку пробной цифры частного осуществляют путем умножения на делитель. Нужно ли в этих случаях произведение вычислять или достаточно только прикинуть его границы?
    
11. 
    В каких учебных ситуациях, по вашему мнению, можно и даже очень полезно предложить учащимся выполнить деление многозначных чисел на калькуляторе?
    
12. 
    Известно, что чаще всего учащиеся допускают ошибки в тех случаях письменного деления, когда в частном получаются нули (в середине или в конце). Какие методические приемы способствуют предупреждению подобных ошибок?
    

СХЕМА №20

МЕТОДИКА ИЗУЧЕНИЯ АЛГЕБРАИЧЕСКОГО МАТЕРИАЛА
Формирование ВУ и ВН. Развитие математической речи, логического, а также тео-

Обобщение знаний о числах, о свойствах арифметических теоретического мышления. Функциональная пропедевтика.

действий, о зависимостях между… Подготовка к дальнейшему изучению математики

записать, прочитать, вычислить, сравнить, преобразовать, доказать, составить по тексту задачи и наоборот

числовые


Математические выражения


с переменной





прочитать, определить значение истинности (верно или неверно), доказать, преобразовать неравенства в равенства


числовые


Равенства и неравенства



с переменной




записать, прочитать, решить (?способы), составить по тексту задачи

1. уравнения


2. тождества




вывести, прочитать, объяснить, применить

3. неравенства с переменной

3 см P - ?

4см S - ?




прочитать, решить способом подбора