дидактические материалы. Дидактические материалы по МПМ в нач. кл.. В. Н. Медведская Дидактические материалы по методике преподавания математики в начальных классах
 Скачать 1.28 Mb. Скачать 1.28 Mb.
|
ПРЕДИСЛОВИЕ Неравнодушный к своему делу молодой специалист, приступив к самостоятельной работе в школе, нередко начинает ощутимо осознавать недостатки и пробелы своей профессиональной подготовки. Обратившись за помощью и поддержкой к опытным коллегам, он иногда слышит совет: "Забудь всё, чему тебя учили". Звучит в нём отнюдь не пренебрежение к знаниям, не отрицание роли науки, а житейская мудрость: жизнь так сложна и многогранна, что для решения даже очень сходных практических задач не существует уже готового шаблона в виде заученных истин. В повседневной деятельности необходимы не догмы, а умелое, гибкое и творческое оперирование теоретическими знаниями. В связи с этим исключительную значимость для изучения любой частной методики приобретает психологическая установка студента. В методику следует "отправляться" не за готовой продукцией в виде указаний, что и как надо делать в одной или другой учебной ситуации (как в лес по грибы или ягоды), а за "инструментами" познания и за способами их разумного применения. Методическая наука – это не свод общепринятых законов, правил и не сборник проверенных педагогической практикой рекомендаций, рецептов, которыми надо неукоснительно руководствоваться при рассмотрении с учащимися того или иного вопроса школьной программы. Поэтому и работа с учебными пособиями по методике принципиально отличается от работы, например, с книгами "Уголовный кодекс", "Фармакология" и т.п. Усвоение методических знаний идёт совсем другими путями и способами: опора не на память, а на мышление, включение не механизмов запоминания, а глубокой аналитическо-синтетической переработки изучаемого материала на основе установления причинно-следственных связей методики со своими базовыми науками (психология, дидактика, математика) и выявления её существенных внутренних связей. Главный результат такой переработки учебной информации – психологическая и теоретическая готовность к действиям в постоянно изменяющихся условиях, т.е. к творческой профессиональной деятельности. Для её характеристики обычно выделяют следующие критерии: – гибкость ума, т.е. способность к выделению существенных признаков из множества случайных, способность варьировать идеи и быстро перестраиваться с одной идеи на другую; – систематичность и последовательность, т.е. способность анализировать известные идеи и сводить их в определённую систему, подвергать эти идеи преобразованию для нахождения решения конкретной методической задачи; – диалектичность мышления, т.е. способность видеть противоречия, формулировать их и находить способ разрешения; – самостоятельность и ответственность в принятии решений. Развивать в себе эти способности поможет в определённой мере и данное пособие, потому что выполнение тестов (раздел 2) непосредственно связано с анализом изучаемого материала и выделением в нём существенного и несущественного, с его перегруппировкой и преобразованием, с применением приобретённых знаний для решения частных методических задач. Но особую роль в этом процессе профессионального становления могут сыграть структурно-логические схемы (будем их называть также опорными) для изучения почти всех тем из программы курса "Методика преподавания математики в начальных классах" (раздел 1). Работа с ними начинается с изучения учебных пособий по методике математики и продолжается при выполнении заданий к каждой схеме. Это создаёт условия не только для продуктивного усвоения учебной информации, но и для осознанного непроизвольного запоминания самих схем, что поможет в воспроизведении соответствующего программного вопроса на экзамене. А глубокое осмысление и достигнутое в ходе многократного обращения к схемам понимание внутренних и внешних, логических, функциональных и структурных связей в изученном материале, надеемся, облегчит поиск профессионально грамотных и ответственных решений конкретных учебных задач в предстоящей самостоятельной работе в школе. Опорные схемы в пособии предлагаются уже в готовом виде. Следует, однако, иметь в виду, что каждая из них является лишь одним из возможных вариантов структурирования изучаемой темы. Приобретя определённый опыт использования схем, каждый сможет предпринять собственные поиски конструирования других наглядно-схематических изображений той или иной темы курса методики преподавания математики в начальных классах, а возможно и других учебных дисциплин. Раздел 3 «Конспекты фрагментов уроков» представляет собой практико-ориентированную составляющую данного пособия. Словарь терминов методики преподавания математики в начальных классах (раздел 4) является дидактическим средством, организующим усвоение научной лексики. Основными задачами данного пособия являются: управление самостоятельной работой студентов; обеспечение её соответствующими дидактическими материалами; содействие осмысленному освоению и систематизации обобщённого в методической науке педагогического опыта, который изложен в различных учебных пособиях по методике; формирование у будущего учителя начальных классов позиции творческого использования приобретаемых знаний; побуждение студентов к самостоятельному поиску конструктивных решений как частных, так и общих проблем начального обучения математике. 1. СТРУКТУРНО-ЛОГИЧЕСКИЕ СХЕМЫ ДЛЯ ИЗУЧЕНИЯ КУРСА МЕТОДИКИ ПРЕПОДАВАНИЯ МАТЕМАТИКИ В НАЧАЛЬНЫХ КЛАССАХ И ЗАДАНИЯ К НИМ Структурно-логические схемы являются специфическим средством наглядности и служат дидактическими ориентирами в изучении соответствующих вопросов. При разработке таких схем сначала путем обобщения принципиально сходных элементов знаний по конкретной теме создаются укрупненные единицы учебной информации, а затем между ними устанавливаются логические и функциональные связи. Полученная таким образом целостная дидактическая система знаний фиксируется в графической или в другой компактной форме, удобной для восприятия, осмысления, запоминания и последующего воспроизведения. Благодаря этому структурно-логические схемы расширяют объем внимания, обеспечивают его целенаправленность, облегчают анализ, синтез и обобщение приобретаемых студентами знаний, отражают структуру учебного материала и дают возможность мысленно исследовать ее рациональность. Средством, организующим понимание и усвоение запрограммированной в каждой схеме информации, являются задания к ним. Форма предъявления заданий обеспечивает выделение тех элементов знаний и отношений между ними, которые могли бы оказаться вне поля внимания студентов. Таким образом, задания к структурно-логическим схемам выполняют многообразные функции: организующую, координирующую, частично информационную, интегрирующую, а также функции контроля и самоконтроля. Последовательное выполнение заданий призвано содействовать повышению качества знаний и постепенному переходу от просто ориентировки в учебном материале к его творческому применению для решения конкретных задач обучения младших школьников математике. Приступая к работе с каждой из опорных схем, следует предварительно изучить соответствующую тему в учебном пособии по методике преподавания математики в начальных классах, установить, соответствует ли предложенная схема содержанию темы, сформулировать к схеме несколько вопросов вида: "Почему...?", "Как изображено...?". В дальнейшем изложении для краткости вместо термина "структурно-логическая схема" будем использовать термин "опорная схема". Такая замена терминов вполне оправдана не только соображениями экономности текста, но и той ролью, которую могут выполнять данные схемы – служить опорой восприятия, внимания, мышления (понимания), памяти. СХЕМА №1 МЕТОДИКА ПРЕПОДАВАНИЯ МАТЕМАТИКИ В НАЧАЛЬНЫХ КЛАССАХ КАК НАУКА 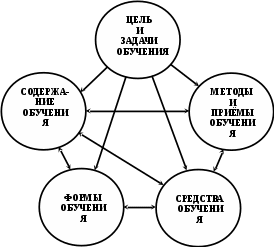 Задания к схеме №1 Назовите компоненты методической системы. На какие вопросы дает ответ методическая наука? Что на схеме означают стрелки? Почему от целей и задач стрелки только выходят? Почему все другие стрелки являются двухсторонними (обратимыми)? Отвечает ли методика преподавания математики на вопрос "Кого учить?" Какие из компонентов методической системы входят в содержание понятия "технология начального обучения математике"? Назовите отличительные признаки технологии развивающего обучения. Составьте план ответа на любой вопрос, формулировка которого начинается словами: «Методика изучения…». СХЕМА №2 СВЯЗЬ МЕТОДИКИ ПРЕПОДАВАНИЯ МАТЕМАТИКИ С ДРУГИМИ НАУКАМИ 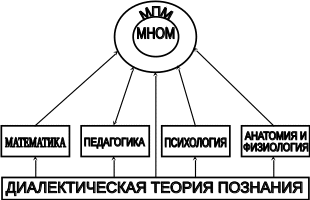 Задания к схеме №2 Почему методику преподавания математики только с педагогикой связывает двухсторонняя стрелка? Почему все остальные стрелки направлены только вверх – к методике преподавания математики? Какими блоками (науками) можно дополнить схему? Объясните. Что составляет методологическую основу всех наук? Приведите конкретные примеры взаимосвязи методики преподавания математики с логикой, психологией, анатомией и физиологией человека. Каким образом математическая наука влияет на методику начального обучения математике? Попытайтесь схематически изобразить взаимосвязь методики преподавания математики в начальных классах с другими науками с помощью кругов Эйлера. В каком отношении находятся всевозможные пары представленных здесь множеств? Объясните, почему? Дополните вашу схему кругом – множеством, пересечение которого с методикой преподавания математики пусто. Каким наукам, на ваш взгляд, он мог бы соответствовать? СХЕМА №3 НАЧАЛЬНЫЙ КУРС МАТЕМАТИКИ КАК УЧЕБНЫЙ ПРЕДМЕТ 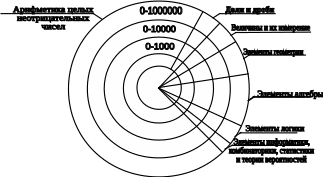 Задания к схеме №3 Что обозначает круг наибольшего диаметра? Почему сектор "Арифметика целых неотрицательных чисел" имеет наибольшую площадь? Назовите другие компоненты содержания начального курса математики. Какие из них можно отнести к традиционным? В пособии "Математика" для первого класса найдите по одному примеру заданий, которые можно отнести к элементам комбинаторики, логики, информатики, теории вероятностей. Какие из принципов построения начального курса математики нашли наглядное отражение в схеме? Сравните по составу содержания традиционный начальный курс математики и предлагаемый в белорусских учебниках. Верно ли, что обновление начального курса математики в Республике Беларусь пошло по следующим направлениям: а) расширение традиционного содержания; б) включение элементарных сведений из относительно новых в историческом аспекте математических наук? Каким образом в связи с таким обновлением содержания можно избежать перегрузки детей? В чем состоит сущность принципа органического единства арифметического материала с другими компонентами содержания начального курса математики? СХЕМА № 4 УТОЧНЕНИЕ ПРОСТРАНСТВЕННЫХ ПРЕДСТАВЛЕНИЙ   2) НАД, ПОД, ВВЕРХУ, ВНИЗУ, СЛЕВА, СПРАВА. ВЕРХНИЙ ПРАВЫЙ УГОЛ И Т.П.  3)  ВНУТРИ, ВНЕ, ЗА.  4) Задания к схеме №4 Назовите термины, характеризующие порядковые отношения. Линейное расположение последовательности предметов в этом случае обязательно? Какие термины учащиеся учатся правильно понимать и употреблять в работе с прямоугольной таблицей? Какие новые термины учащиеся учатся правильно понимать и употреблять, работая с одним обручем? Приведите примеры заданий разного вида для работы учащихся в прямоугольной таблице, для работы с одним обручем. Проиллюстрируйте в предметной деятельности с набором геометрических фигур справедливость законов Какие логические операции учатся выполнять учащиеся, характеризуя свойства множеств, образуемых при заполнении таблиц или кругов геометрическими фигурами, а также другим дидактическим материалом? СХЕМА № 5 ОБУЧЕНИЕ СРАВНЕНИЮ МНОЖЕСТВ 1   ) НА ГЛАЗ (ПО МЕСТУ, ЗАНИМАЕМОМУ НА ПЛОСКОСТИ) ) НА ГЛАЗ (ПО МЕСТУ, ЗАНИМАЕМОМУ НА ПЛОСКОСТИ)НАЛОЖЕНИЕ ПРИЛОЖЕНИЕ  СОЕДИНЕНИЕ ЛИНИЯМИ ИСПОЛЬЗОВАНИЕ МНОЖЕСТВА ПОСРЕДНИКА СЧЁТ  2  ) СТОЛЬКО ЖЕ АВС n(А)= =n(В)=n(С)=4 ) СТОЛЬКО ЖЕ АВС n(А)= =n(В)=n(С)=4 3) АВ Б М Б на … М на … 4 больше, чем 3 на 1, а 3 меньше, чем, 4 на 1 4) РАЗНООБРАЗИЕ УПРАЖНЕНИЙ 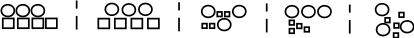 5   ) УРАВНИВАНИЕ МНОЖЕСТВ ) УРАВНИВАНИЕ МНОЖЕСТВЗадания к схеме №5 Назовите способы сравнения множеств. Почему в дочисловой период операция счета не может быть использована для ответа на вопрос: "Чего больше (меньше)?" С какой целью в дочисловой период сравнение, выполненное способом непосредственного образования пар элементов заданных множеств, полезно сопровождать счетом? В  какой последовательности вводятся отношения "больше", "меньше", "столько же"? Почему? какой последовательности вводятся отношения "больше", "меньше", "столько же"? Почему?Что в схеме означает запись Б М ? Ч 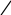 то означает запись: АВС => "столько же", А В => "больше", "меньше"? то означает запись: АВС => "столько же", А В => "больше", "меньше"?Назовите два способа уравнивания численности множеств. Докажите, что требования "достаточно много" и "разнообразные упражнения" являются необходимыми условиями для формирования умения сравнивать множества. Какие отношения между множествами являются прообразом отношений "равно", "больше", "столько же", "одинаково", "поровну", "меньше" между натуральными числами? Почему в схеме не используются общепринятые знаки "=", ">'', "''? Предложите упражнения в сравнении множеств с целью введения и первичного закрепления понятий "столько же", "больше", "меньше". Назовите общие и отличительные признаки таких упражнений. Проиллюстрируйте разнообразие видов заданий на сравнение множеств, отличительными признаками которых являются: а) состав элементов (неоднородные, однородные); б) характеристические свойства (размер, цвет, назначение и т.п.); в) пространственное размещение элементов (по горизонтали, по вертикали, произвольное). Какие дидактические функции выполняют упражнения на уравнивание множеств по их численности? В схеме отражены два основных способа уравнивания численности множеств. Возможны ли другие способы? При каком условии? Приведите соответствующие примеры. СХЕМА № 6 ОБУЧЕНИЕ СЧЁТУ I  ПОДГОТОВИТЕЛЬНАЯ РАБОТА ПОДГОТОВИТЕЛЬНАЯ РАБОТА а) A = x P(x) ; A U B ; Aв ; n(A) n(B) б) один, два, три, . . . . II ОБУЧЕНИЕ СЧЁТУ о   дин, два, три, четыре, пять, шесть… дин, два, три, четыре, пять, шесть…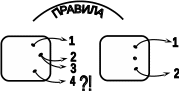 А  КСИОМА СЧЁТА: КСИОМА СЧЁТА: П 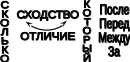 1 П 2 1 П 2III ФОРМИРОВАНИЕ УМЕНИЯ СЧИТАТЬ Достаточно много. Разнообразные. Во всех концентрах Задания к схеме № 6 Прочитайте первую строку в схеме и дайте теоретико-множественное толкование содержанию работы на подготовительном этапе? Зачем ученикам надо предлагать задания вида: "Покажите всё желтые фигуры "и ". Как одним словом можно назвать все эти предметы? " Приведите примеры заданий разного рода, которые связаны с подготовкой детей к счету. Назовите виды заданий, помогающих детям запомнить последовательность имен чисел первого десятка. Найдите в схеме определение операции счета. Сформулируйте правила счета. Имеют ли они место для порядкового счета? С помощью двух слов охарактеризуйте особенности работы на этапе формирования навыка счета. Дайте соответствующее обоснование. Ч   то на схеме обозначает символ ? то на схеме обозначает символ ?В чем отличие порядкового и количественного счета? На основе анализа определения и правил счета выявите возможные затруднения и ошибки учащихся при счете. Предложите такие упражнения в счете, чтобы при их выполнении могла возникнуть проблемная ситуация, разрешение которой ведет к открытию и формулированию правил счета. Как вы понимаете методическое требование: "Правила и аксиома счета устанавливаются практически"? Приведите примеры упражнений в счете, отличительными признаками которых являются: а) состав элементов множеств (однородные, неоднородные); б) характеристическое свойство (цвет, размер, назначение и т.п.); в) пространственное размещение (линейное, по замкнутому контуру, по иным конфигурациям); г) опора на различные анализаторы (органы чувств), выполняющие ведущую роль при счете; д) единицы счета (счет парами, тройками и т.п.); е) опора на представление множества, элементы которого пересчитываются. Исходя из теоретико-множественного определения понятия "натуральное число", а также из психологических особенностей младших школьников, докажите, что упражнения в счете должны быть разнообразны. СХЕМА №7 КЛАССИФИКАЦИЯ АРИФМЕТИЧЕСКИХ ЗАДАЧ В НКМ  Задания к схеме №7 По какому признаку арифметические задачи делятся на простые и на составные? По какому признаку многообразие всех простых задач делят на 3 большие группы? Почему в первую группу простых задач входят 5 типов, а не 4 (ведь арифметических действий всего 4!)? Назовите термины, которые обязательно есть в условии или вопросе задач, относящихся ко второй группе? Докажите, не перечисляя типы задач, что ко второй группе простых задач относится 12 типов. Докажите чисто логическим путем, что в третью группу простых задач должно входить именно 8 типов. Назовите 3 основных типа составных задач с пропорциональными величинами. Простыми или составными являются задачи следующих типов: на встречное движение, на совместную работу? Можно ли отнести их к задачам с пропорциональными величинами? Есть ли другие типы составных задач? Существуют ли составные задачи, не относящиеся ни к одному из известных вам типов? Зачем учителю знать классификацию арифметических задач? Следует ли учащимся, на ваш взгляд, знать названия типов задач и уметь подводить конкретную задачу под соответствующий тип? Возможна ли классификация всех составных задач? Проведите классификацию простых арифметических задач по способу их решения, т.е. по используемому в решении арифметическому действию. Проанализируйте следующую схему. по а взяли с раз ? по а взяли с раз значит, надо умножать I – а, это в с раз меньше. II – ? если в I в с раз меньше, чем во II, то во II в с раз больше чем в I. Значит, надо умножать I – а II – ?, в с раз больше во II по а взяли с раз. Значит надо умножать 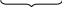      х : а = с чтобы найти неизвестное делимое, надо частное умножить на делитель  В какой последовательности могут вводиться эти задачи при теоретико-множественном подходе в трактовке смысла арифметических действий. СХЕМА № 8 МЕТОДИКА ОБУЧЕНИЯ РЕШЕНИЮ ПРОСТЫХ ЗАДАЧ, РАСКРЫВАЮЩИХ СМЫСЛ АРИФМЕТИЧЕСКИХ ДЕЙСТВИЙ I. ПОДГОТОВИТЕЛЬНАЯ РАБОТА а) операции над множествами 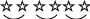 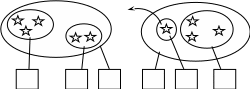 2 3 6 2 (по) 6 3 (на) 3 2 = ? 4 1 = ? б 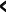      ) ) в) овладение приёмами сложения и вычитания и заучивание таблиц II ОЗНАКОМЛЕНИЕ СО СПОСОБОМ РЕШЕНИЯ |
