Уменьшаемое Вычитаемое Разность
5 — 2 = 3
Задания к схеме №20
Назовите задачи изучения алгебраического материала в начальном обучении математики.
Перечислите алгебраические понятия, включаемые в содержание начального курса математики.
Фрагменты листа школьной тетради в клеточку напоминают вам о необходимости конкретизировать каждое из этих понятий. Приведите такие примеры числовых выражений, выражений с переменной, числовых равенств и неравенств, уравнений, тождеств, неравенств с переменной, чтобы в каждом их наборе нашел отражение общий принцип обучения "от простого к сложному".
В начальном обучении математике ни одно из алгебраических понятий не доводится до уровня их формального определения. Какие вопросы в связи с этим не следует задавать учащимся?
Формирование правильных представлений о каждом из перечисленных в данной схеме алгебраических понятий осуществляется в практической деятельности с соответствующим математическим материалом. Назовите виды упражнений, выполняя которые учащиеся уясняют смысл понятий "числовое выражение", "выражение с переменной".
Что в данной опорной схеме обозначают прямоугольники? Найдите прямоугольник, относящийся к понятиям "числовое равенство" и "числовое неравенство". Охарактеризуйте виды практических действий с этими понятиями и приведите конкретные примеры.
Что в данной схеме обозначают овалы и стрелки, соединяющие их с тем или другим прямоугольником? Какими уже обобщенными, т.е. теоретическими знаниями пользуются учащиеся при определении значений истинности числовых равенств или неравенств (например, 23<32, 9·8 < 9·3, 8·4=8·3+8, 22<53-38, 51-13 >60)?
Какую информацию дает нижний ряд данной опорной схемы?
Рассмотрите верхний овал. О каких терминах и математических символах здесь идет речь? Какие демонстрационные средства наглядности используются для обеспечения запоминания учащимися названий компонентов и результатов арифметических действий? Есть ли образец такого средства наглядности в заданной схеме? Предложите аналогичные для сложения, умножения и деления.
Знание математических терминов и символов необходимо учащимся для того, чтобы записывать и читать сначала математические выражения, а затем и составленные из них разного вида равенства и неравенства. Укажите практическое применение в работе с математическими выражениями других теоретических знаний, перечисленных в верхнем овале.
Сколькими способами вы сами можете прочитать, например, выражение 12:3? Какими знаниями вы при этом пользуетесь? Следует ли учить детей читать выражения разными способами? Почему?
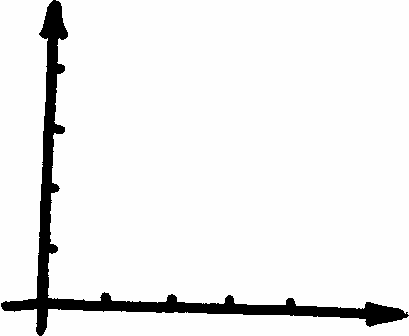
Найдите в данной схеме изображение абака с подвижной лентой. Для каких целей можно использовать подобные средства наглядности? В чем состоит конкретный смысл понятия "переменная"? Способствует ли решение уравнений и неравенств с переменной способом подбора формированию у детей представления о переменной?
Назовите способы решения уравнений в начальном курсе математики. Какие знания необходимы учащимся, чтобы решать уравнения каждым из этих способов?
Определите дидактические функции заданий по заполнению прямоугольных таблиц, аналогичных приведенной в нижнем ряду данной опорной схемы.
Охарактеризуйте содержание подготовительной работы к решению уравнений на основе знания зависимостей между компонентами и результатами арифметических действий.
Проанализируйте решение неравенств 70204>у>70199 и 120:а<3 и выделите знания и умения, которые формируются, закрепляются и совершенствуются в процессе выполнения учащимися таких заданий.
Арифметические понятия, например, "натуральное число", "сложение" и другие вводятся путем абстрагирования непосредственно из действительности. При введении же алгебраических понятий в качестве наглядности используются разного вида математические записи, а не реальные объекты или их модели. Чем можно объяснить такой подход?
Можно ли утверждать, что изучение алгебраического материала вносит существенный вклад в развитие абстрактного мышления учащихся, в развитие математической речи и математического стиля мышления? Свой ответ проиллюстрируйте конкретными примерами.
Найдите в данной опорной схеме графическую модель уравнения х+3=9. Постройте аналогичные модели для уравнений на нахождение неизвестного уменьшаемого и неизвестного вычитаемого. Удобно ли использовать отрезки для моделирования уравнений, содержащих действия умножения и деления? Какую модель для них вы можете предложить.
Охарактеризуйте место и значение в начальном курсе математики алгебраического способа решения текстовых задач.
Назовите типы арифметических задач, при решении которых учащиеся знакомятся с прямой и обратной пропорциональной зависимостью, т.е. с функциями у=k⁄x и у=к/х.
СХЕМА № 21
МЕТОДИКА ИЗУЧЕНИЯ ГЕОМЕТРИЧЕСКОГО МАТЕРИАЛА
№
п/п
| Содержание |
Рекомендуемые методы и приёмы
|
Деятельность учащихся (мыслительная и практическая)
| Результаты изучения | Применение |
1
|
2
|
3
|
4
|
5
|
6
|
1
| П о н я т и я

|
объяснительно-иллюстративный, варьирование несущественных признаков
|
анализ, синтез, сравнение, конкретизация, классификация; находят, показывают, моделируют, считают, вычисляют, называют
|
термины и их геометрические образы
|
в жизни, для счёта, в обучающих играх, для моделирования арифметических понятий
|
2
|
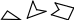
 многоугольник многоугольник
|
частично-поиско-вый, демонстрация, варьирование несущественных признаков, сопоставление, эвристическая беседа, самостоятельная работа
|
анализ, синтез, сравнение, абстрагирование, обобщение, конкретизация, аналогия; дают название, распознают, классифицируют, моделируют, чертят, доказывают
|
термины, существенные признаки сходства многоугольников из одного класса, доказательства, геометрическая форма предметов и их частей
|
при изучении нумерации, при анализе формы сложных фигур, при построении чертежей, для обучения предматематическим доказательствам
|
3
|
|
объяснительно-иллюстративный, самостоятельная практическая работа
|
анализ, синтез; находят, показывают, называют, отрывают углы, моделируют, вычерчивают, считают, измеряют
|
термины и их геометрические образы: вершина (точка), сторона (отрезок), угол, умение пользоваться линейкой
|
при анализе многоугольников, при построении чертежей
|
4
|
|
частично-поисковый, моделирование, варьирование несущественных признаков, противопоставление
|
сравнивают, называют, находят, моделируют, рисуют, чертят
|
термины и их геометрические образы, отличительные свойства
|
в жизни, при построениях, на уроках изоискусства, при письме цифр и букв
|
5
|
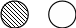
|
объяснительно- иллюстративный, практическая работа, противопоставление
|
показывают, называют, находят, моделируют, строят
|
термины и их геометрические образы, признаки, отличия, умение пользоваться циркулем
|
для развития математически грамотной речи, для дальнейшего изучения геометрии, при построении, при чтении и построении диаграмм
|
6
|

|
частично-поисковый, моделирование, варьирование несущественных признаков, сравнение, обобщение
|
изготавливают модели, сравнивают, делают индуктивный вывод
|
термин и его геометрический образ, свойство прямых углов, умение пользоваться угольником
|
для классификации углов, треугольников, четырёхугольников, при построении
|
7
|
длина периметр
|
объяснительно-иллюстративный, моделирование, эвристическая беседа
|
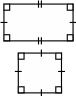
анализ, синтез, сравнение, конкретизация, дедуктивные умозаключения; находят, моделируют, называют, измеряют, вычисляют длину ломаной и периметр
|
термины и их геометрические образы, определение периметра многоугольника
|
в жизни, при решении задач на вычисление периметра, для формирования вычислительных навыков, для обучения дедуктивным рассуждениям
|
8
|
|
частично-поисковый, построение, демонстрация, варьирование несущественных признаков, сравнение (углов и сторон), практическая работа, эвристическая беседа
|
анализ, синтез, сравнение, индуктивные умозаключения; измеряют, перегибают, наблюдают, обобщают, строят, доказывают, находят в окружающей обстановке
|
определения, родовидовые отношения, свойства сторон, способы вычисления периметра и площади, дедуктивные доказательства
|
в жизни, при построении, при решении вычислительных задач
|
9
|
|
объяснительно-иллюстративный, сравнение (сторон)
|
анализ, синтез, сравнение, классификация; измеряют стороны, называют, распознают, моделируют, чертят, доказывают
|
определения, чтение чертежей, дедуктивные доказательства
|
при построении, при решении задач на вычисление периметра, для дедуктивных предматематических доказательств и развития математического стиля мышления
|
В
С А
10
|
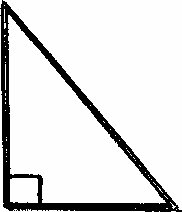 
|
объяснительно-иллюстративный, сравнение (углов)
|
анализ, синтез, сравнение, классификация; сравнивают углы с моделью прямого угла, называют, находят, моделируют, чертят, доказывают
|
определения, чтение чертежей, дедуктивные доказательства
|
при построении, при анализе чертежей, для дедуктивных доказательств и развития математического мышления
|
11
|
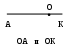
|
объяснительно-иллюстративный, варьирование несущественных признаков, противопоставление
|
называют, вычленяют на чертеже, сравнивают с отрезком и прямой, чертят, доказывают
|
определение, геометрический образ, отличительные признаки
|
при построении и чтении чертежей, для подготовки к изучению курса геометрии
|
12
|
Отношения
на множестве геометрических фигур: “одинаковые”–“разные” (по форме)
|
частично-поисковый, демонстрация, варьирование несущественных признаков, сопоставление
|
анализ, синтез; сравнение, абстрагирование, конкретизация; сравнивают (на глаз, по числу элементов), классифицируют, находят, чертят, доказывают
|
умение классифицировать по форме
|
для счёта, в повседневной жизни, при анализе чертежей, для моделирования дробей, при введении геометрических понятий
|
13
|
на множестве геометрических величин (длина, площадь, величина угла): “рав-но”-”больше“-”меньше“
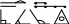
|
объяснительно–иллюстративный, сравнение, моделирование
|
сравнивают (на глаз, наложением, путём измерения), чертят, моделируют, доказывают
|
пространственное воображение, моделирование отношений ”больше“-”меньше“-“равно” с помощью отрезков
|
в повседневной жизни, при введении геометрических понятий, единиц измерения длины и площади, для моделирования текстовых задач
|
14
|
Н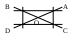 а множестве прямых: “║” ,┴”, “пересечение” а множестве прямых: “║” ,┴”, “пересечение”
|
объяснительно–иллюстративный, сравнение
|
анализ, синтез, сравнение, конкретизация, дедуктивные умозаключения; находят, называют, чертят, доказывают
|
определения, чтение чертежей, дедуктивные доказательства
|
при построении и чтении чертежей, для предматематических доказательств и подготовки к изучению курса геометрии
|
1 5 5
| П ОСТРОЕНИЕ ОСТРОЕНИЕ
на на
на на
Без учёта размеров и с учётом размеров
|
практическая работа
|
анализ, синтез, подведение под понятие; строят, измеряют, контролируют, доказывают
|
пространственные представления, навыки пользования чертёжными инструментами
|
в жизни, при изучении нумерации, приёмов сложения и вычитания, при моделировании свойств сложения и вычитания, для подготовки к изучению курса геометрии
|
16
| ИЗМЕРЕНИЕ
длины, периметра, площади

|
лабораторно-практическая работа
|
сравнивают на глаз, наложением, с помощью посредника, путём инструментальных измерений
|
навыки использования измерительных инструментов
|
в жизни, при построении чертежей, на уроках трудового обучения, для расширения понятия натурального числа
|
17
|
К  ОНСТРУИРОВАНИЕ И ПРЕОБРАЗОВАНИЕ ОНСТРУИРОВАНИЕ И ПРЕОБРАЗОВАНИЕ
|
практическая работа
|
разрезают, составляют новые фигуры, разбивают на чертеже на указанные части, вычленяют, считают, строят
|
пространственное воображение, представление о равновеликих и равносоставленных фигурах,о геометрических преобразованиях
|
в жизни, для подготовки к изучению курса геометрии, на уроках трудового обучения, для развития творческого мышления
|
18
| В ЫЧИСЛЕНИЕ ЫЧИСЛЕНИЕ |
частично-поисковый, эвристическая беседа
|
находят рациональный способ и выводят правила (формулы), применяют их при решении текстовых задач
|
правила (формулы) для нахождения периметра и площади прямоугольника (квадрата)
|
в жизни, для моделирования свойств умножения, для формирования вычислительных навыков, для обучения дедуктивным рассуждениям
| |
 Скачать 1.28 Mb.
Скачать 1.28 Mb.

 многоугольник
многоугольник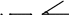



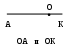
 а множестве прямых: “║” ,┴”, “пересечение”
а множестве прямых: “║” ,┴”, “пересечение” 5
5 ОСТРОЕНИЕ
ОСТРОЕНИЕ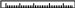


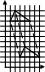 ОНСТРУИРОВАНИЕ И ПРЕОБРАЗОВАНИЕ
ОНСТРУИРОВАНИЕ И ПРЕОБРАЗОВАНИЕ  ЫЧИСЛЕНИЕ
ЫЧИСЛЕНИЕ