Занимательные задачи для 5-6 классов. В семье четверо детей. Им 5, 8, 13 и 15 лет, а зовут их Аня, Юра, Света и Лена. Сколько лет каждому из них, если одна девочка ходит в детский сад, Аня старше, чем Юра, а сумма лет Ани и Светы делится на три
 Скачать 182.5 Kb. Скачать 182.5 Kb.
|
|
часть страны. Учащимся достаточно показать, что съедено менее половины всех жителей. Оксана сказала, что чашку разбила Соня. Лена и Соня сказали, кто разбил чашку, но каждая говорила очень тихо и их не услышали. Известно, что одна из трех девочек разбила чашку, и только она и сказала правду. Как ее зовут? Ответ объясните. Ответ. Лена. Раз одна из трех девочек разбила чашку, и только она и сказала правду, то эта девочка призналась в том, что именно она разбила чашку. Оксана говорила не о себе, значит, она сказала неправду. А это означает, что чашку не могла разбить ни Оксана, ни Соня. Рядом сидят мальчик и девочка. «Я мальчик», — говорит черноволосый ребенок. «Я девочка», — говорит рыжий ребенок. Выясните цвет волос мальчика и цвет волос девочки, если известно, что хотя бы кто-то из них обязательно говорит неправду. Ответ. Очевидно, что если лжет один ребенок, то лжет и другой. Поэтому черноволосый ребенок — девочка, рыжий ребенок — мальчик. В одной сказке хозяин, нанимая работника, предложил ему испытание: «Вот тебе бочка, наполни ее водой ровно наполовину, не испольвуя никаких измерительных приборов». Работник исполнил задание. Как он это сделал? Ответ. Нужно наклонить бочку, как показано на рисунке. Объем воды под горизонтальной чертой равен половине объема бочки. 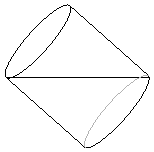 Имеются два пустых бидона — трехлитровый и пятилитровый. Как, пользуясь этими бидонами, набрать из реки 1 л воды? Ответ. Один из способов показан в таблице:
Сошлись два пастуха, Иван и Петр. Иван и говорит Петру: «Отдай-ка ты мне 1 овцу, тогда у меня овец будет вдвое больше, чем у тебя"! А Петр ему отвечает: "Нет! Лучше ты мне отдай одну овцу, тогда у нас будет овец поровну"! Сколько же было у каждого овец? Ответ. У Ивана — 7 овец, а у Петра — 5 овец. Как бы вы назвали известный роман Жюля Верна «20 000 лье под водой» в существующих ныне единицах длины (1 морское лье = - 5 км 555 м)? Ответ. 111 100 км под водой. «Ну, погоди!» — зарычал волк, заметив в 30 м зайца, бросился за ним, когда тому оставалось до места укрытия 333 м. Догонит ли волк зайца, если он пробегает за минуту 600 м, а заяц — 550 м? Ответ обоснуйте. Ответ. Да догонит. Скорость сближения волка и зайца 50 м/мин. Значит, волку, чтобы догнать зайца, надо Двое часов начали и закончили бить одновременно. Первые бьют через каждые 2 с, вторые — через каждые 3 с. Всего было сделано 13 ударов (совпавшие удары воспринимались за один). Сколько времени прошло между первым и последним ударами? Ответ. 18 с. В морской порт теплоход «Счастливый» прибывает один раз в 3 дня, теплоход «Удачный» - один раз в 4 дня, теплоход «Надежный» — один раз в 6 дней. Третьего марта все три теплохода были в этом порту. Какого числа они все снова прибудут в этот порт? Ответ. 15 марта. По улице шла Катя. Встретив старичка, она поздоровалась. Старичок в ответ сказал: «Здравствуй, маленькая девочка». Катя возразила: «Я не маленькая. Я в три раза младше мамы, а мама на 2 года младше отца. Вместе нам 100 лет». Так сколько лет Кате? Ответ. 14 лет. Над цепью озер летела стая гусей. На каждом озере садилась половина имевшегося в этот момент количества гусей и еще полгуся, а остальные летели дальше. Все гуси сели на семи озерах. Сколько гусей было в стае? Ответ. 127 гусей. Не трудно догадаться, что на седьмое озеро сел один гусь. И тогда: на шестое озеро прилетело 3 гуся, из которых 2 осталось на этом озере, до пятого озера долетело 7 гусей, до четвертого - 15, до третьего - 31, до второго - 63, до первого - 127 гусей. Валя и Таня должны были встретиться на станции, чтобы вместе поехать на поезде, который отправляется в 8 ч утра. Валя думает, что ее часы спешат на 35 мин, хотя в действительности они отстают на 15 мин. А Таня думает, что ее часы идут правильно, хотя они на самом деле отстают. На сколько минут отстают часы Тани, если две девочки пришли на станцию одновременно? И когда они встретились? Ответ. На 50 мин. девочки встретятся в 8 ч 50 мин. Вася вырвал три листа из дневника. Некоторые из них (может быть и все) он разорвал на три части или на пять частей. Некоторые из получившихся кусков бумаги он опять разорвал на три или пять частей, и так далее. Мог ли Вася, действуя таким образом, получить ровно 2000 кусочков бумаги? Ответ объясните. Ответ. Нет, не мог. Если разорвать любой лист бумаги натри части, то количество кусков увеличится на 2, а если его разорвать на пять частей, то количество кусков увел ичится на 4. Так как было три листа, то после каждого действия Васи количество кусочков бумаги останется нечетным, следовательно, получится ровно 2000 кусочков не может. Двое мальчиков катались на лодке. К берегу подошёл отряд солдат. Лодка так мала, что на ней могли переправиться двое мальчиков или только один солдат. Смогли ли солдаты переправиться через реку? Ответ. Мальчики на лодке плывут к другому берегу. Один из них остается там, а другой возвращается. Один солдат переправляется; вылезает, а мальчик возвращает лодку. Таким образом, чтобы переправить одного солдата, лодка 4 раза плывёт от берега до берега. Улитка ползёт вверх по столбу высотой 10 м. За день она поднимается на 5 м, а за ночь — опускается на 4 м. За какое время улитка доберётся от подножья до вершины столба? Ответ. Через 5,5 суток. Кот в Сапогах поймал четырех щук и ещё половину улова. Сколько щук поймал Кот в Сапогах? Ответ. 8 щук. Кирпич весит 2 кг и ещё треть собственного веса. Сколько весит кирпич? Ответ. 3 кг. Три слога в слове. Первый слог — Большой снеговика кусок. Осуществляют слог второй Слоны, придя на водопой. А третий слог зовётся так, Как прежде звался твёрдый знак. Соедини все три как надо — Получишь ЭВМ в награду! Ответ. КОМ + ПЬЮТ + ЕР = КОМПЬЮТЕР Три купчихи — Сосипатра Титовна, Олимпиада Карповна и Поликсена Уваровна — сели пить чай. Олимпиада Карповна и Сосипатра Титовна выпили вдвоём 11 чашек, Поликсена Уваровна и Олимпиада Карповна — 15, а Сосипатра Титовна и Поликсена Уваровна — 14. Сколько чашек чая выпили все три купчихи вместе? Ответ. 20 чашек. В книжном шкафу стоят по порядку четыре тома собрания сочинений Астрид Линдгрен, по 200 страниц в каждом томе. Червячок, живущий в этом собрании, прогрыз путь от первой страницы первого тома до последней страницы четвёртого тома. Сколько страниц прогрыз червячок? Ответ. 400 страниц. Зайцы распилили несколько брёвен. Они сделали 10 распилов и получили 16 чурбачков. Сколько брёвен они распилили? Ответ. 6 брёвен. Старый сапожник Карл сшил сапоги и послал своего сына Ганса на базар — продать их за 25 талеров. На базаре к мальчику подошли два инвалида (один без левой ноги, другой — без правой) и попросили продать им по сапогу. Ганс согласился и продал каждый сапог за 12,5 талера. Когда мальчик пришёл домой и рассказал всё отцу, Карл решил, что инвалидам надо было продать сапоги дешевле — каждому за 10 талеров. Он дал Гансу 5 талеров и велел вернуть каждому инвалиду по 2,5 талера. Пока мальчик искал на базаре инвалидов, он увидел, что продают сладости, не смог удержаться и истратил 3 талера на конфеты. После этого он нашёл инвалидов и отдал им оставшиеся деньги — каждому по одному талеру. Возвращаясь домой, Ганс понял, как нехорошо он поступил. Он рассказал всё отцу и попросил прощения. Сапожник сильно рассердился и наказал сына, посадив его в тёмный чулан. Сидя в чулане, Ганс задумался. Получалось, что раз он вернул по одному талеру, то инвалиды заплатили за каждый сапог по 11,5 талера: 12,5 — 1 = 11,5. Значит, сапоги стоили 23 талера: 11,5+'11,5 = 23. И 3 талера Ганс истратил на конфеты, следовательно, всего получается 26 талеров: 23 + 3 = 26. Но ведь было-то 25 талеров! Откуда же взялся лишний талер? Ответ. 3 талера, которые Ганс истратил на конфеты, надо не прибавить к стоимости сапог, а вычесть из неё. Тогда мы получим 20 талеров — ту сумму, которую в итоге получил Карл. Белоснежка вырезала из батиста большой квадрат и положила его в сундук. Пришёл Первый Гном, достал квадрат, разрезал его на четыре квадрата и положил все четыре снова в сундук. Потом пришёл Второй Гном, достал один из квадратов, разрезал его на четыре квадрата и положил все четыре снова в сундук. Потом пришёл Третий Гном. И он достал один из квадратов, разрезал его на четыре квадрата и положил все четыре снова в сундук. То же самое проделали все остальные гномы. Сколько квадратов лежало в сундуке после того, как ушёл Седьмой Гном? Ответ. 22 квадрата. Когда Гулливер попал в Лилипутию, он обнаружил, что там все вещи ровно в 12 раз короче, чем на его родине. Сможете ли вы сказать, сколько лилипутских спичечных коробков поместится в спичечный коробок Гулливера? Ответ. 1728 Коробков. На каждом километре шоссе между сёлами Ёлкино и Палкино стоит столб с табличкой, на одной стороне которой написано, сколько километров до Елкина, а на другой — до Палкина. Вдумчивый Наблюдатель заметил, что на каждом столбе сумма равна 13. Каково расстояние от Ёлкина до Палкина? Ответ. 13 км. За книгу заплатили 100 руб. и осталось заплатить ещё столько, сколько осталось бы заплатить, если бы за неё заплатили столько, сколько осталось заплатить. Сколько стоит книга? Ответ. Книга стоит 200 руб. Эта задача насчитывает много сотен лет, но до сих пор поражает воображение своей красотой и неожиданностью. Три брата получили в наследство от отца 17 верблюдов. Старшему отец завещал половину стада, среднему — треть, а младшему — девятую часть. Братья пытались поделить наследство и выяснили, что старшему брату придётся взять 8 верблюдов и кусок верблюда, среднему — 5 верблюдов и кусок верблюда, а младшему — верблюда и кусок верблюда. Естественно, разрезать верблюдов не хотелось никому, и братья решили попросить помощи у Мудреца, проезжавшего мимо них на верблюде. Мудрец спешился и присоединил своего верблюда к стаду братьев. От нового стада из 18-ти верблюдов Мудрец отделил половину — 9 верблюдов для старшего брата, затем треть — 6 верблюдов для среднего брата, и, наконец, девятую часть — 2-х верблюдов для младшего брата. После успешной делёжки Мудрец сел на своего верблюда и продолжил путь. А братья стали думать, почему же каждый из них получил больше верблюдов, чем полагалось. Сможете ли вы объяснить, что же произошло? Ответ. Наследники с самого начала не заметили, что завещанные им доли составляют не 100%, а всего 17/18 от общего количества. Одно трехзначное число состоит из различных цифр, следующих в порядке возрастания, а в его названии все слова начинаются с одной и той же буквы. Другое трехзначное число, наоборот, состоит из одинаковых цифр, но в его названии все слова начинаются с разных букв. Какие это числа? Ответ. 147 и 111. Путешественник, сняв в гостинице комнату на неделю, предложил хозяину в уплату цепочку из семи серебряных колец — по кольцу за день, с тем, однако, условием, что будет рассчитываться ежедневно. Хозяин согласился, оговорив со своей стороны, что можно распилить только одно кольцо. Как путешественнику удалось расплатиться с хозяином гостиницы? Ответ. Путешественник должен распилить 3-е кольцо. Тогда он получит три звена: первое — из одного кольца, второе — из двух, третье — из четырех. В первый день путешественник даст хозяину гостиницы 1 кольцо. Во второй — даст 2 кольца, заберёт 1. В третий — даст 1 кольцо. В четвёртый — даст 4, заберёт 2 и 1 кольцо. В пятый — даст 1 кольцо. В шестой — даст 2 кольца, заберёт 1. В последний (седьмой) день даст 1 кольцо. Если Конёк-Горбунок не будет семь суток есть или не будет семь суток спать, то лишится своей волшебной силы. Допустим, он в течение недели не ел и не спал. Что он должен сделать в первую очередь к концу седьмых суток — поесть или поспать, чтобы не потерять силу? Ответ. Он должен сделать не то, что делал перед началом отсчёта первых суток. Дядька Черномор написал на листке бумаги число 20. Тридцать три богатыря передают листок друг другу, и каждый или прибавляет к числу или отнимает от него единицу. Может ли в результате получиться число 10? Ответ. Нет, не может. После того как листок побывает в руках у богатыря, число, на нём написанное, будет менять свою чётность, т. е. станет чётным, если было нечётное, и наоборот. Это значит, что после 33-х изменений число станет нечётным, т.е. никак не сможет равняться 10. Имеются чашечные весы, любые гири и десять мешков с монетами. Все монеты во всех мешках одинаковы по внешнему виду, но в одном из мешков все монеты фальшивые и каждая весит по 15 г, а в остальных девяти мешках все монеты настоящие и каждая весит по 20 г. Как при помощи одного взвешивания определить, в каком мешке фальшивые монеты? Ответ. Возьмём из первого мешка 1 монету, из второго — 2, из третьего — 3, ..., из последнего — 10. Взвесим их. Если фальшивая монета в первом мешке — будет не хватать 5 г, если во втором — 10, ... если в последнем — 50 г. Отличник Поликарп купил общую тетрадь объёмом 96 листов и пронумеровал все её страницы по порядку числами от 1 до 192. Двоечник Колька вырвал из этой тетради 25 листов и сложил все 50 чисел, которые на них написаны. В ответе у Кольки получилось 2002. Не ошибся ли он? Ответ. Сумма номеров на одном листе нечётна, поскольку это — сумма двух последовательных чисел. Всего страниц 25. Сумма 25 нечётных чисел должна быть нечётной, а у Кольки получилось чётное число. Значит, Колька ошибся в своих вычислениях. Фома и Ерёма нашли на дороге по пачке 11-рублевок. В чайной Фома выпил 3 стакана чая, съел 4 калача и 5 бубликов. Ерёма выпил 9 стаканов чая, съел 1 калач и 4 бублика. Стакан чая, калач и бублик стоят по целому числу рублей. Оказалось, что Фома может расплатиться 11-рублевками без сдачи. Покажите, что это может сделать и Ерёма. Ответ. Фома смог за свою покупку расплатиться 11-рублёвыми купюрами. Если мы к его покупке добавим 33 ч и 11 б (т. е. 33 стакана чая и 11 бубликов), то за всё в сумме тоже можно будет расплатиться 11-рублевками. Но эта покупка составляет 36 ч + 4 к + 16 б, т. е. ровно в 4 раза больше покупки Еремы. Но числа 4 и 11 взаимно просты, поэтому и за четверть большой покупки (за покупку Еремы) можно расплатиться 11-рублевками без сдачи, что и требовалось доказать. Собрался Иван-царевич на бой со Змеем Горынычем, трехглавым и треххвостым. — Вот тебе меч-кладенец, — сказала царевичу Баба Яга. — Одним ударом ты можешь срубить Змею либо одну голову, либо две головы, либо один хвост, либо два хвоста. Запомни: срубишь голову — новая вырастет; срубишь хвост — два новых вырастут; срубишь два хвоста — голова вырастет; срубишь две головы — ничего не вырастет. За сколько ударов Иван-царевич может срубить Змею Горынычу все головы и все хвосты? |
