Дипломная работа «Формирование познавательных универсальных учебных действий младших школьников в процессе обучения».. Дипломная работа. В современном обществе стремительно развиваются наука и техника, создаются новые информационные технологии, коренным образом меняющие жизнь людей

• Название: В современном обществе стремительно развиваются наука и техника, создаются новые информационные технологии, коренным образом меняющие жизнь людей
• Анкор: Дипломная работа «Формирование познавательных универсальных учебных действий младших школьников в процессе обучения»
• Дата: 05.04.2022
• Размер: 372.01 Kb.
• Имя файла: Дипломная работа.docx
• Тип: Документы; #444283
• страница: 4 из 5

2.3 Динамика сформированности познавательных универсальных учебных действий младшего школьника

Целью контрольного этапа стало выявление динамики развития уровня сформированности познавательных универсальных учебных действий после проведения системы уроков по математике. Для этого мы использовали те же методики, что и на констатирующем этапе:

1. 
   "Диагностика универсального действия общего приёма решения задач" (А.Р. Лурия, Л.С. Цветкова)
   
2. 
   "Нахождение схем к задачам" (А.Н. Рябинкина)
   

В результате проведения первой методики мы видим, что в 3 классе повысился уровень сформированности приёма решения задач. Полученные данные были оформлены в общую таблицу (табл. 3) и отражены в диаграмме.

Таблица 3

Результаты повторного проведения методики "Диагностика универсального действия общего приёма решения задач" (А.Р. Лурия, Л.С. Цветкова)

Уровни	Кол-во учащихся	%
Низкий	1	8%
Средний	3	25%
Высокий	8	67%

Процентное соотношение результатов повторного проведения методики "Диагностика универсального действия общего приёма решения задач" (А.Р. Лурия, Л.С. Цветкова) показано на рисунке 3.

Рисунок 3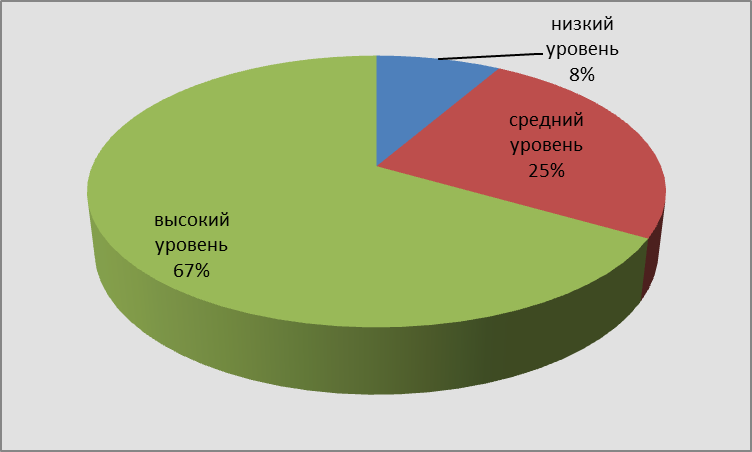


В результате проведения второй методики мы также наблюдаем некоторые изменения, которые представлены в таблице 4. Мы можем сделать вывод, что разработанная система уроков позволила испытуемым экспериментальной группы освоить действие моделирования.

Таблица 4

Результаты повторного проведения методики "Нахождение схем к задачам" (А.Н. Рябинкина)

Уровни	Кол-во учащихся	%
Низкий	1	8%
Средний	4	34%
Высокий	7	58%

Процентное соотношение результатов повторного проведения методики "Нахождение схем к задачам" (А.Н. Рябинкина) показано на рисунке 4

Рисунок 4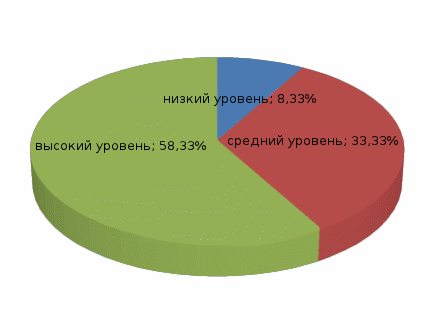


В связи с полученными результатами мы можем судить об общем повышении познавательных универсальных учебных действий.

Полученные результаты позволяют говорить о положительной динамике формирования уровня познавательных универсальных учебных действий.
Обобщённые результаты можно увидеть в таблице 5

Таблица 5

Процентное соотношение результатов

Диагностики	Низкий уровень		Средний уровень		Высокий уровень
	Перв.	Втор.	Перв.	Втор.	Перв.	Втор.
Диагностика универсального действия общего приёма решения задач" (А.Р. Лурия, Л.С. Цветкова)	33%	8%	50%	25%	17%	67%
"Нахождение схем к задачам" (А.Н. Рябинкина)	25%	8%	42%	34%	33%	58%

По данным контрольной диагностики можно сделать вывод о том, что уровень сформированности познавательных универсальных учебных действий учащихся значительно повысился по сравнению с первичной диагностикой.

Выводы по 2 главе

Экспериментальную работу по формированию познавательных универсальных учебных действий мы разделили на три этапа: констатирующий, формирующий и контрольный.

Констатирующий этап был связан с определением наличного уровня сформированности познавательных универсальных учебных действий младших школьников. Уровень сформированности универсальных учебных действий учащихся (высокий, средний, низкий) в нашем исследовании был избран в качестве интегрального критерия. Результаты констатирующего этапа позволяют нам с достаточной степенью уверенности утверждать о преобладании низкого и среднего уровней.

Формирующий этап направлен на формирование познавательных универсальных учебных действий на уроках математики в 3 классе, с помощью решения задач и действие моделирования.

Контрольный этап был посвящен оценке достигнутого уровня сформированности познавательных универсальных учебных действий учащихся.

Полученные результаты математической статистики подтвердили наше предположение, что формирование познавательных универсальных учебных действий в процессе обучения математике в начальной школе будет происходить эффективнее, если:

-применение общего приёма решения задач и действие моделирования, направлено на формирование познавательных УУД младших школьников в процессе обучения математике;

- применение общего приёма решения задач и действие моделирования, направленные на развитие познавательных универсальных учебных действий будет систематическим.

Заключение

Актуальность исследования проблемы формирования универсальных учебных действий (УУД) у младших школьников обусловлена изменением образовательной парадигмы в соответствии с логикой компетентностного подхода: от цели усвоения учащимся конкретных предметных ЗУН( знаний, умений, навыков) в рамках отдельных учебных дисциплин к цели развития познавательных способностей школьников, обеспечивающих у них такую ключевую компетенцию, как умение учиться и благоприятствующих их саморазвитию и самосовершенствованию. Достижение данной цели становиться возможным благодаря формированию учащихся системы универсальных учебных действий как эффективного средства обучения на уроках математики.

Проблема эффективного формирования универсальных учебных действий обучающихся – одна из сложных и противоречивых проблем современной педагогической науки. С одной стороны, она отражает потребность общества, выраженную в образовательном заказе на учащихся, способных к полноценной самореализации, самостоятельному добыванию знаний и эффективному осуществлению различного рода деятельности; показывает заинтересованность учёных в нахождении путей формирования надпредметных действий школьников. С другой стороны, отражено, что современная система школьного образования с традиционной организацией учебного процесса и соответствующим методическим обеспечением ещё не готова справиться с объективными факторами, которые определяют формирование общепознавательных действий учащихся, и грамотно, на научной основе, обеспечить формирование надпредметных действий младших школьников в оценочной деятельности.

В ходе теоретического и экспериментального исследования в дипломной работе были решены все поставленные задачи.

На основе анализа психологической, педагогической, методологической литературы по изучаемой проблеме и изучения современного состояния практики образования были определены теоретические предпосылки формирования универсальных учебных действий у младших школьников. Проведённое исследование доказало наличие рассматриваемой проблемы и указало на её недостаточную изученность в теории, в практике современного образования.

Сравнительно – сопоставительный анализ научной литературы по проблеме исследования позволил уточнить содержание понятия "познавательные универсальные учебные действия младших школьников ". Под " универсальными учебными действиями младших школьников" мы понимаем совокупность обобщённых действий учащегося, а также связанных с ними умений и навыков учебной работы, обеспечивающих способность субъектов к самостоятельному усвоению новых знаний, умений и компетентностей, к сознательному и активному присвоению нового социального опыта, к саморазвитию и самосовершенствованию".

В основу дипломной работы положена классификация универсальных учебных действий, предложенная разработчиками федерального государственного образовательного стандарта второго поколения.

В ходе изучения научной литературы было установлено, что универсальный характер познавательных действий проявляется в том, что они:

1) носят надпредметный и метапредметный характер;

2) лежат в основе организации и регуляции любой деятельности учащегося независимо от её специально – предметного содержания;

3) обеспечивают этапы усвоения учебного содержания и формирования психологических способностей учащегося;

4) обеспечивают целостность общекультурного, личностного и познавательного развития, саморазвития и самосовершенствования личности.

Интегративный характер способности к саморазвитию позволяет определить систему универсальных учебных действий как ключевую компетенцию, обеспечивающую у учащихся как " умение учиться". Основы формирования " умение учиться" закладываются в период начального обучения ребёнка в школе: полученный в это время опыт предопределяет успешность обучения учащихся в течение всей последующей жизни.

Математика как школьный предмет имеет большие потенциальные возможности для формирования всех видов УУД. Реализация этих возможностей на этапе начального математического образования зависит от способов организации учебной деятельности младших школьников, которые позволяют не только обучать математике, но и воспитывать математикой, не только учить мыслям, но и учить мыслить.

Одним из эффективных способов формирования познавательных УУД является включение в работу специальной системы заданий, в нашем случае нестандартных логических задач, повышающее познавательный интерес младших школьников на уроках математики, обладающее значительным воспитательным потенциалом, создающее зону ближайшего развития для всех учащихся.

Гипотеза данного исследования подтверждена.формирование познавательных универсальных учебных действий в процессе обучения математике в начальной школе будет происходить эффективнее, если:

- применение общего приёма решения задач и действие моделирования, направлено на формирование познавательных УУД младших школьников в процессе обучения математике;

- применение общего приёма решения задач и действие моделирования, направленные на развитие познавательных универсальных учебных действий будет систематическим.

Список литературы:

1. 
   Асмолов, А.Г. «Формирование универсальных действий: от действия к мысли» / А.Г. Асмолов, Г.В. Бурменская. – М.: просвещение, 2010. – 159 c.
   
2. 
   Бордовская Н.В. Педагогика: учебное пособие. /Н.В.Бордовская, А.А.Реан. – Гриф МО. – СПб.: Питер, 2008. – 299 с..
   
3. 
   Василевский А.Б. Обучение решению задач поматематике.  М., Просвещение, 2001. - 406 с.
   
4. 
   Видинеев Н.В. Природа интеллектуальных способностей человека. - М., 2006. – 173 c.
   
5. 
   Возрастная и педагогическая психология: учебно-методический комплекс в 2 частях. Часть 1: учебное пособие по возрастной и педагогической психологии / О. В. Кузьменкова, М. М. Елфимова, М. Н. Олекс и др.; под ред. О. В. Кузьменковой. — Оренбург: Изд-во ОГПУ, 2005. — 288 с.
   
6. 
   Гальперин П.Я., Кабыльницкая С.Л. Экспериментальное формирование внимания. М.: Издательство Московского Университета, 2000. 124 с.
   
7. 
   Григорьева Г.И. Логика. Занимательные материалы для развития логического мышления. 3 класс. - Учитель - АСТ, 2004. - 112с.
   
8. 
   Давыдов В.В. Теория развивающего обучения М.,ИНТОР, 1996 г. – 544 с.
   
9. 
   Еланская З.А. Активизация познавательной деятельности // Начальная школа. - 2001. - №6. - С.52 - 54.
   
10. 
    Зайцев Т.Г. Теоретические основы обучения решению задач в начальной школе. – М.: Педагогика, 2002. – 99 с.
    
11. 
    Зак А.З. 600 игровых задач для развития логического мышления детей. - Ярославль: Академия развития, 2004. - 192с.
    
12. 
    Зак А.З. Развитие умственных способностей младших школьников. М.: Просвещение, Владос, 2005. – 102 с.
    
13. 
    Истомина Н.Б. Активизация учащихся на уроках математики в начальных классах: Пособие учителя. М.,: Просвещение, 2002. – 64 с.
    
14. 
    Как проектировать универсальные учебные действия в начальной школе. От действия к мысли: пособие для учителя / [А. Г. Асмолов, Г. В. Бурменская, И. А. Володарская]; под ред. А. Г. Асмолова. — М.: Просвещение, 2011. — 152 с.
    
15. 
    Канцева М.Н. Развитие младших школьников в теории и практике начального обучения. Оренбург. Изд.ООИУУ, 2003 г.  – 35 с.
    
16. 
    Керова Г.В. Нестандартные задачи по математике 1 - 4 классы. Москва: ВАКО, 2008. - 237с.
    
17. 
    Крайг Г., Бокум Д. Психология развития. — СПб.: Питер, 2005. — 940 с.
    
18. 
    Крутецкий В. А. Психологические особенности младшего школьника / Возрастная и педагогическая психология: учебно-методический комплекс в 2 частях. Часть 2: Хрестоматия по возрастной и педагогической психологии / под ред. О. В. Кузьменковой. — Оренбург: Изд-во ОГПУ, 2005. — 240 с.
    
19. 
    Лихтарников Л.М. Занимательные логические задачи. Для учащихся начальной школы. - СПб.: "Лань", "Мик", 1996. – 125 с.
    
20. 
    Люблинская А.А. Учителю о психологии младшего школьника М., «Просвещение» 2007 г.  – 224 с.
    
21. 
    Матюхина М. В., Михальчик Т. С., Прокина Н. Ф. Возрастная и педагогическая психология. — М.: Просвещение, 2009.—256с.
    
22. 
    Мухина В. С. Возрастная психология. Феноменология развития. — М.: Издательский центр «Академия», 2006. — 608 с.
    
23. 
    Мельникова Т. А. и др. Математика. Развитие логического мышления 1-4 классы. Комплекс упражнений и задач. Волгоград: « Учитель» , 2011 г. – 131 с.
    
24. 
    Оценка достижения планируемых результатов в начальной школе: Система заданий: В 3 ч. Ч.1 / под ред. Г. С. Ковалевой, О. Б. Логиновой. - М.: Просвещение, 2011. – 215 с.
    
25. 
    Павлова Т.Л. Диагностика мышления младших школьников. ТЦ «Сфера». 2006. – 64 с.
    
26. 
    Педагогический энциклопедический словарь./ под ред. Л.М.Лузиной. Псков: ПГПИ, 2003 – 71 с.
    
27. 
    Планируемые результаты начального общего образования / под ред. Г. С. Ковалевой, О. Б. Логиновой. - М.: Просвещение, 2011. – 120 с.
    
28. 
    Примерная основная образовательная программа образовательного учреждения. Основная школа / [сост. Е.С. Савинов]. — М.: Просвещение, 2011. — 342 с.
    
29. 
    Репкин В.В. Формирование учебной деятельности в младшем школьном возрасте. «Начальная школа», №7 – 2003 г.
    
30. 
    Репкина Н.В. Что такое развивающее обучение? – Научно-популярный. - Томск: Пеленг. 2002 г. – 60 с.
    
31. 
    Рождественская Н. В., Толшин А. В. Креативность: пути развития и тренинги. — СПб.: Речь, 2006. — 320 с.
    
32. 
    Стратегия модернизации содержания общего образования. Материалы для разработки документов по обновлению общего образования. – М.: ООО «Мир книги», 2001. – 95 с.
    
33. 
    Сухин И.Г. 800 новых логических и математических головоломок. – СПб.: Альфа, 1998. – 164 с.
    
34. 
    Тихомирова Л.Ф., Басов А.В. Развитие логического мышления детей. - Ярославль: ТОО Академия развития, 2008. - 240с.
    
35. 
    Тонких А.П., Кравцова Т.П., Лысенко Е.А., Стогова Д.А., Голощапова С.В. Логические игры и задачи на уроках математики. - Ярославль: Академия развития, 1997. - 240 с.
    
36. 
    Ушинский К.Д. Человек предмет воспитания. Собрание сочинений. М., 1979 г.
    
37. 
    Федеральный образовательный стандарт начального общего образования. - М.: Просвещение, 2010.- 251 с.
    
38. 
    Формирование универсальных учебных действий в основной школе. От действия к мысли. Система заданий: пособие для учителя / [А. Г. Асмолов, Г. В. Бурменская, И. А. Володарская]; под ред. А. Г. Асмолова. — М.: Просвещение, 2011. — 159 с.
    
39. 
    Царева С.Е. Нестандартные виды работы с задачами на уроке как средство реализации современных педагогических концепций и технологий // Начальная школа. - 2004. - №4. - С. 49 - 51.
    
40. 
    Эльконин Д.Б. Избранные  психологические труды/ Д.Б. Эльконин. – М.:Педагогика, 1989. - 560 с.
    

Приложение 1.

Диагностика универсального действия общего приема решения задач

(по А. Р. Лурия, Л. С. Цветковой)

Цель: выявление сформированности общего приема реше­ния задач.

Оцениваемые универсальные учебные действия: прием решения задач; логические действия.

Возраст: 6,5—10 лет.

Метод оценивания: индивидуальная или групповая рабо­та детей.

Описание задания: все задачи (в зависимости от возраста учащихся) предлагаются для решения арифметическим (не ал­гебраическим) способом. Допускаются записи плана (хода) решения, вычислений, графический анализ условия. Учащий­ся должен рассказать, как он решал задачу, доказать, что по­лученный ответ правильный.

Критерии оценивания: умение выделять смысловые еди­ницы текста и устанавливать отношения между ними, созда­вать схемы решения, выстраивать последовательность опера­ций, соотносить результат решения с исходным условием за­дачи.

Уровни сформированности общего приема решения за­дач:

1. При анализе задачи выделяют не только существенные, но и несущественные смысловые единицы текста; создают не­адекватные схемы решения; применяют стереотипные спосо­бы решения; не умеют соотносить результат решения с ис­ходным условием задачи.

2. При анализе выделяют только существенные смысловые единицы текста; при создании схемы решения не учитывают все связи между данными условия и требованием; применя­ют стереотипные способы решения; испытывают трудности (допускают ошибки) в соотнесении результата решения с ис­ходными данными задачи.

3. При анализе выделяют только существенные смысловые единицы текста; создают различные схемы решения; используют разные способы решения; обосновывают соответствие полученных результатов решения исходному условию задачи. А.Р. Лурия и Л.С. Цветкова предложили набор задач с постепенно усложняющейся структурой, который дает воз­можность диагностировать сформированность обобщенного способа решения задач.

1. Наиболее элементарную группу составляют простые за­дачи, в которых условие однозначно определяет алгоритм ре­шения, типа а + Ь = х или а — Ь = х. Например:

• У Маши 5 яблок, а у Пети 4 яблока. Сколько яблок у них обоих?

• Коля собрал 9 грибов, а Маша — на 4 гриба меньше, чем Коля. Сколько грибов собрала Маша?

• В мастерскую привезли 47 сосновых и липовых досок. Липовых было 5 досок. Сколько сосновых досок привезли в мастерскую?

2. Простые инвертированные задачи типа а — х = Ь или х — а = Ь, существенно отличающиеся от задач первой груп­пы своей психологической структурой. Например:

• У мальчика было 12 яблок; часть из них он отдал. У не­го осталось 8 яблок. Сколько яблок он отдал?

• На дереве сидели птички. 3 птички улетели; осталось 5 птичек. Сколько птичек сидело на дереве?

3. Составные задачи, в которых само условие не опреде­ляет возможный ход решения, типа а + (а + Ь) = х или а + (а – Ь) = х. Например:

У Маши 5 яблок, а у Кати на 2 яблока больше (мень­ше). Сколько яблок у них обеих?

• У Пети 3 яблока, а у Васи в 2 раза больше. Сколько яблок у них обоих?

4. Сложные составные задачи, алгоритм решения которых распадается на значительное число последовательных опера­ций, каждая из которых вытекает из предыдущей, типа а + (а + Ь) + [(а + Ь) — с] = х. Например:

• Сын собрал 15 грибов. Отец собрал на 25 грибов боль­ше, чем сын. Мать собрала на 5 грибов меньше отца. Сколь­ко всего грибов собрала вся семья?

• У фермера было 20 га земли. С каждого гектара он снял по 3 т зерна. 1/2 зерна он продал. Сколько зерна осталось у фермера?

5. Сложные задачи с инвертированным ходом действий, од­на из основных частей которых остается неизвестной и долж­на быть получена путем нескольких операций. Например:

• Сыну 5 лет. Через 15 лет отец будет в 3 раза старше сы­на. Сколько лет отцу сейчас?

• Одна ручка и один букварь стоят 37 рублей. Две ручки и один букварь стоят 49 рублей. Сколько стоят отдельно од­на ручка и один букварь?

• Три мальчика поймали 11 кг рыбы. Улов первого и вто­рого был 7 кг; улов второго и третьего — 6 кг. Сколько ры­бы поймал каждый из мальчиков?

• Отцу 49 лет. Он старше сына на 20 лет. Сколько лет им обоим вместе?

6. Задачи на прямое (обратное) приведение к единице, на разность, на части, на пропорциональное деление. Например:

• 15 фломастеров стоят 30 рублей. Купили 8 таких фло­мастеров. Сколько денег заплатили?

• Купили кисточек на 40 рублей. Сколько кисточек купи­ли, если известно, что 3 такие кисточки стоят 24 рубля?

• Надвухполкахстояло 18 книг. На одной из них было на 2 книги больше. Сколько книг было на каждой полке?

• Двое мальчиков хотели купить книгу. Одному не хвата­ло для ее покупки 7 рублей, другому не хватало 5 рублей. Они сложили свои деньги, но им все равно не хватило 3 рублей. Сколько стоит книга?

• По двору бегали куры и кролики. Сколько было кур, если известно, что кроликов было на 6 больше, а у всех вмес­те было 66 лап?

Существенное место в исследовании особенностей развития интеллектуальной деятельности имеет анализ того, как учащийся приступает к решению задачи и в каком виде стро­ится у него ориентировочная основа деятельности. Необходимо обратить внимание на то, как ученик составляет план или общую схему решения задачи, как составление предваритель­ного плана относится к дальнейшему ходу ее решения. Кроме того, важным является анализ осознания проделанного пути и коррекция допущенных ошибок, а также фиксация обучающей помощи при затруднениях во время выполнения уроков учащегося и анализ того, как он пользуется помощью, насколько продуктивно взаимодействует со взрослым.

Приложение 2

Методика «Нахождение схем к задачам»

(noA.H. Рябинкиной)

Цель: определение умения ученика выделять тип задачи и способ ее решения.

Оцениваемые универсальные учебные действия: модели­рование, познавательные логические и знаково-символические действия.

Возраст: 7—9 лет.

Метод оценивания: фронтальный опрос или индивиду­альная работа с детьми.

Описание задания: учащемуся предлагается найти со­ответствующую схему (рис. 4, 5) к каждой задаче. В схемах числа обозначены буквами. Предлагаются следующие за­дачи:

1. Миша сделал 6 флажков, а Коля — на 3 флажка боль­ше. Сколько флажков сделал Коля?

2. На одной полке 4 книги, а на другой — на 7 книг боль­ше. Сколько книг на двух полках?

3. На одной остановке из автобуса вышли 5 человек, а на другой вышли 4 человека. Сколько человек вышли из авто­буса на двух остановках?

4. На велогонке стартовали 10 спортсменов. Во время со­ревнования со старта сошли 3 спортсмена. Сколько велоси­педистов пришли к финишу?

5. В первом альбоме 12 марок, во втором — 8 марок. Сколько марок в двух альбомах?