Обратимые и необратимые процессы. В термодинамике для описания состояния систем, состоящих из большого числа атомов и молекул, используются макроскопические величины, например давление, температура, объем, внутренняя энергия и др
 Скачать 387.88 Kb. Скачать 387.88 Kb.
|
|
Введение В термодинамике для описания состояния систем, состоящих из большого числа атомов и молекул, используются макроскопические величины, например давление, температура, объем, внутренняя энергия и др. Эти понятия вводятся на основе физического эксперимента, он же является основой всех закономерностей, обуславливающих их связь между собой для конкретных макроскопических систем - газов, жидкостей или твердых тел. Одна из важнейших задач теории и эксперимента - нахождение уравнения состояния вещества. В школьном курсе физики хорошо известно уравнение состояния идеального газа: 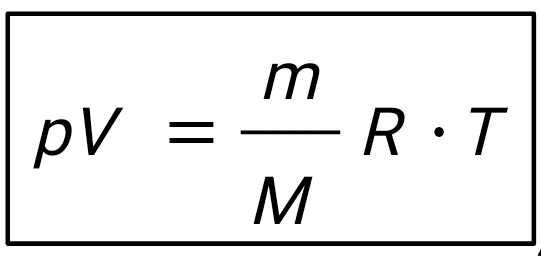 ,(1) ,(1)связывающее его давление р и объем V с массой m, молярной массой М, абсолютной температурой Т и универсальной газовой постоянной R. Важно подчеркнуть, что это уравнение справедливо для газа, находящегося в состоянии термодинамического равновесия, когда давление и температура по всему объему одинаковы. Для смеси разных газов, содержащихся в некотором объеме, давление определяется суммой парциальных давлений газов - закон Дальтона. Этот закон выполняется при условии не только равенства температур газов, но и однородности смеси по всему объему. С известными ограничениями - не очень большая плотность, не очень низкие или высокие, по сравнению с «нормальными», температуры - уравнение состояния идеального газа используется для описания реальных газов, в том числе многоатомных. Часто оно же применяется и для типично неравновесных систем - таких, например, как земная атмосфера. Хотя в реальной атмосфере с высотой сложным образом изменяются давление, температура и химический состав газов, уравнение состояния достаточно точно описывает ее поведение на какой-то высоте или в небольшом объеме - например, в пределах одной комнаты. Отметим, наконец, что уравнение состояния идеального газа используют для описания поведения паров, в том числе и насыщенных. При этом необходимо отчетливо понимать, чем ограничены возможности такого описания. Так, для насыщенного пара, если он таковым остается в течение всего процесса, давление определяется только температурой, причем для разных жидкостей величины давлений при одних и тех же температурах могут сильно отличаться. Однако с помощью уравнения состояния можно найти, например, массу пара в данном объеме, если известны давление и температура. Важное значение в термодинамике имеет понятие квазистатического, или обратимого процесса изменения состояния макроскопической системы. В ходе такого процесса состояние системы должно изменяться так медленно, чтобы каждое промежуточное состояние было равновесным. Обратимый процесс допускает возможность возвращения системы в первоначальное состояние через ту же последовательность промежуточных состояний, что и в прямом процессе. Основным законом, описывающим обратимые процессы, является закон сохранения энергии - первое начало термодинамики: Q = ∆U + A,(2) Здесь Q - подведенное в процессе количество теплоты. ∆U - изменение внутренней энергии системы и А - работа системы против внешнего давления. Внутренняя энергия системы - функция состояния, так что если начальное и конечное состояния системы равновесны, то изменение внутренней энергии не зависит от процесса перехода системы между ними. Для идеального газа внутренняя энергия зависит только от температуры: 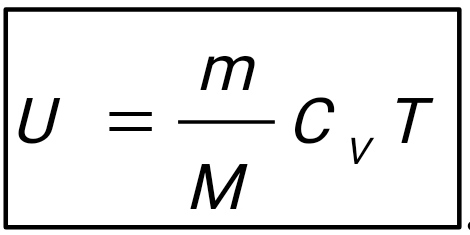 .(3) .(3)Коэффициент СV называют молярной теплоемкостью при постоянном объеме. Для одноатомного газа он равен ЗR/2, а для двухатомного 5R/2. Работа и подведенное количество теплоты существенно зависят от способов перевода системы из начального состояния в конечное. Более того, изобразить процесс наглядно, например, в виде графика зависимости давления от объема системы, и вычислить работу по известным формулам возможно только для обратимых процессов. Ввиду важности адиабатического процесса приведем вывод его уравнения для идеального газа. Закон сохранения энергии в адиабатическом процессе, записанный для двух Близких состояний, отличающихся по температуре и объему на малые величины dT и dV, имеет вид 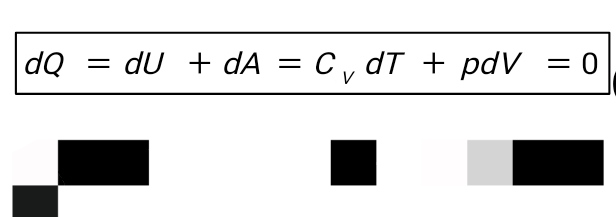 (4) (4)Используя уравнение состояния для моля газа pV = RT, имеем: 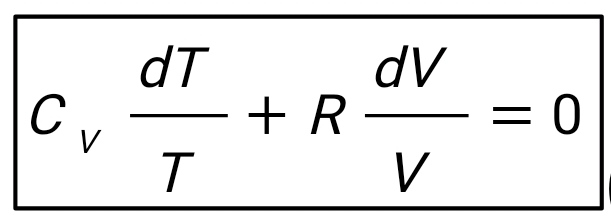 (5) (5)Вспомним формулу для производной логарифмической функции: 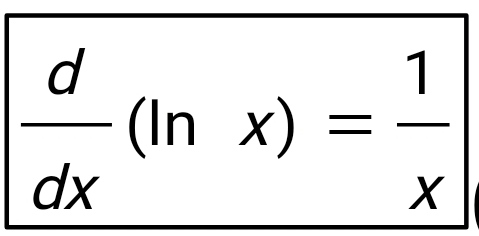 (6) (6)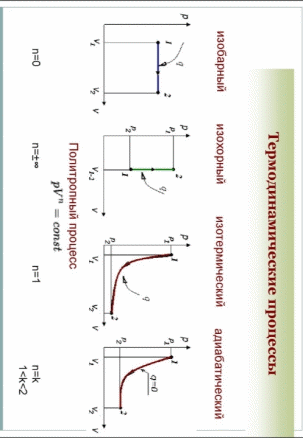 Термодинамический процесс представляет непрерывное изменение состояний системы, которое происходит в итоге ее взаимодействий с окружающей средой. Внешним признаком процесса будет считаться в таком случае изменение хотя бы одного параметра состояния. Реальные процессы изменения состояния проистекают при условии присутствия значительных скоростей и разностей потенциалов (давлений и температур), существующих между системой и средой. В подобных условиях появится сложное неравномерное распределение параметров и функций состояния, исходя из объема системы, пребывающей в неравновесном состоянии. Термодинамические процессы, предусматривающие прохождение системы через ряд неравновесных состояний, будут называться неравновесными. Изучение неравновесных процессов считается сложнейшей для ученых задачей, поскольку разработанные в рамках термодинамики методы приспособлены в основном для исследования равновесных состояний. К примеру, неравновесный процесс весьма сложно рассчитывается посредством уравнений состояния газа, применимых для равновесных условий, в то время, как в отношении всего объема системы давление и температура обладают равными значениями. Возможно было бы выполнять приближенный расчет неравновесного процесса путем подстановки в уравнение средних значений параметров состояния, но в большинстве случаев осреднение параметров по объему системы становится невозможным. В технической термодинамике в рамках исследования реальных процессов условно принимают распределение параметров состояния равномерным образом. Это, в свою очередь, позволяет воспользоваться уравнениями состояния и иными расчетными формулами, полученными с целью равномерного распределения в системе параметров. В некоторых конкретных случаях погрешности, обусловленные подобным упрощением, незначительны и при расчете реальных процессов их возможно не учитывать. Если в результате неравномерности процесс ощутимо отличается от идеальной равновесной модели, то в расчет внесут соответствующие поправки. Условия равномерно распределенных параметров в системе при изменении ее состояния, по существу подразумевают взятие идеализированного процесса в качестве объекта исследования. Подобный процесс при этом состоит из бесконечно большого количества равновесных состояний. Такой процесс возможно представить в формате протекающего настолько медленно, что в каждый конкретный момент времени в системе установится практически равновесное состояние. Степень приближения такого процесса к равновесному окажется тем большей, чем меньшей будет при этом скорость изменения системы. В пределе мы приходим к бесконечно медленному процессу, предоставившему непрерывную смену для состояний равновесия. Подобный процесс равновесного изменения состояния будет называться квазистатическим (или как бы статическим). Такому виду процесса будет соответствовать бесконечно малая разность потенциалов между системой и окружающей средой. При обратном направлении квазистатического процесса система будет проходить через состояния, аналогичные тем, что происходят в прямом процессе. Такое свойство квазистатических процессов называют обратимостью, а сами процессы при этом являются обратимыми.  Обратимый процесс (равновесный) – представляет термодинамический процесс, способный к прохождению и в прямом, и в обратном направлении (за счет прохождения через одинаковые промежуточные состояния), система при этом возвращается в исходное состояние без энергетических затрат, а в окружающей среде не остается никаких макроскопических изменений. Обратимый процесс возможно в абсолютно любой момент времени заставить протекать в обратном направлении, за счет изменения какой-либо независимой переменной на бесконечно малую величину. Обратимые процессы могут давать наибольшую работу. Большую работу от системы получить невозможно ни при каких условиях. Это придает теоретическую важность обратимым процессам, реализовать которые на практике также нереально. Такие процессы протекают бесконечно медленно, и становится возможным лишь приблизиться к ним. Важно отметить существенное отличие термодинамической обратимости процесса от химической. Химическая обратимость будет характеризовать направление процесса, а термодинамическая – способ, при котором он будет проводиться. Понятия обратимого процесса и равновесного состояния играют очень значимую роль в термодинамике. Так, каждый количественный вывод термодинамики будет применим исключительно в отношении равновесных состояний и обратимых процессов. Необратимые процессы термодинамики Необратимый процесс невозможен к проведению в противоположном направлении посредством все тех же самых промежуточных состояний. Все реальные процессы считаются в физике необратимыми. В качестве примеров таких процессов выступают следующие явления: Диффузия — явление, при котором происходит взаимное проникновение молекул или атомов одного вещества между частицами другого. Термодиффузия — термодинамический эффект, который приводит к появлению в смеси градиента концентрации компонентов постоянных изменений температуры. Теплопроводность — способность материальных объектов проводить (теплоту) от более нагретых частей к менее нагретым путем диффузии. Вязкое течение — течение вещества, при котором взаимодействие отдельных его частей приводит к совершению работы и уменьшению энергии. Переход кинетической энергии (для макроскопического движения) в теплоту через трение (во внутреннюю энергию системы) будет представлять собой необратимый процесс. Все осуществляемые в природе физические процессы подразделяются на обратимые и необратимые. Пусть изолированная система вследствие некоего процесса осуществит переход из состояния А в состояние В и затем возвратится в свое изначальное состояние. Процесс, в таком случае, станет обратимым в условиях вероятного осуществления обратного перехода из состояния В в А через аналогичные промежуточные состояния таким путем, чтобы при этом не оставалось совершенно никаких изменений в окружающих телах. Если осуществление подобного перехода невозможно и при условии сохранения по окончании процесса в окружающих телах или внутри самой системы каких-либо изменений, то процесс окажется необратимым. Любой процесс, сопровождающийся явлением трения, станет необратимым, поскольку, в условиях трения, часть работы всегда превратится в тепло, оно рассеется, в окружающих телах сохранится след процесса – (нагревание), что превратит процесс (с участием трения) в необратимый. Идеальный механический процесс, выполняемый в консервативной системе (без сил трения), стал бы обратимым. Примером подобного процесса можно считать колебания на длинном подвесе тяжеловесного маятника. По причине незначительной степени сопротивления среды, амплитуда маятниковых колебаний становится практически неизменной на протяжении продолжительного времени, кинетическая энергия колеблющегося маятника при этом оказывается полностью переходящей в его потенциальную энергию и обратно. В качестве важнейшей принципиальной особенности всех тепловых явлений (где участвует громаднейшее количество молекул), будет выступать их необратимый характер. Примером процесса такого характера можно считать расширение газа (в частности, идеального) в пустоту. Итак, в природе наблюдается существование двух видов принципиально различных процессов: Обратимых; Необратимых. Согласно заявлению М. Планка, сделанного однажды, различия между такими процессами, как необратимые и обратимые, будут лежать значительно глубже, чем, к примеру, между электрическими и механическими разновидностями процессов. По этой причине, его с большим основанием (сравнительно с любым другим признаком) имеет смысл выбирать как первейший принцип в рамках рассмотрения физических явлений. 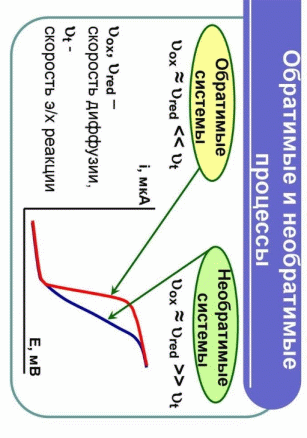 Литература 1.Шеронов А., Обратимые и необратимые процессы в термодинамике. 2.https://spravochnick.ru/fizika/termodinamika/obratimye_i_neobratimye_processy_v_termodinamike/#termodinamicheskiy-process План: Введение Термодинамические процесс Обратимые процессы Необротимые процессы Литература |
