тер мех 25 вариант. В виде плоского многозвенного механизма изображена на рисунке 5 в масштабе 1 10

• Название: В виде плоского многозвенного механизма изображена на рисунке 5 в масштабе 1 10
• Анкор: тер мех 25 вариант
• Дата: 02.11.2022
• Размер: 0.76 Mb.
• Имя файла: zadanie_2.docx
• Тип: Документы; #767342

Постановка задачи. Механическая система в виде плоского многозвенного механизма изображена на рисунке 5 в масштабе 1:10.

Механизм состоит из шести подвижных звеньев различной формы, установленных в неподвижном цилиндрическом корпусе. В точках А, В, К, М соответствующие звенья соединены между собой шарнирами.

Два колеса с неподвижными осями вращения О₁ и О₂

кинематически связаны между собой намотанной на них нитью. Третье колесо катится по неподвижной цилиндрической поверхности корпуса без проскальзывания, при этом его подвижная ось В движется по дуге окружности радиусом СВ. Ползун перемещается по криволинейной направляющей корпуса так, что его точка М движется по дуге окружности радиусом СМ.

Ведущее колесо механизма вращается вокруг неподвижной оси О₁, перпендикулярной плоскости рисунка с постоянным угловым ускорением ε1,

. имея в указанном на рисунке положение угловую скорость ω1.

Дано:

ω₁  3

_с-1_,

ε₁  5

с^-2, положительное направление отсчета

угла поворота φ₁ ведущего колеса – против хода часовой стрелки.

Требуется:

1. 
   Определить для заданного положения механизма скорости точек А, В, D, Е, К, М и угловые скорости звеньев механизма с помо- щью мгновенных центров скоростей;
   
2. 
   Определить для заданного положения механизма аналити- ческим методом ускорения точек А, В, D и угловое ускорение звена ABD.
   

Определение скоростей точек и угловых скоростей звеньев

По заданной отрицательной величине угловой скорости

ω₁ с

учетом принятого положительного направления отсчета угла φ₁ уста-навливаем, что ведущее колесо вращается вокруг неподвижной осиО₁ по часовой стрелке. Поэтому на кинематической схеме механизма

изображаем угловую скорость го направления (рис.6).

ω₁ дуговой стрелкой соответствующе-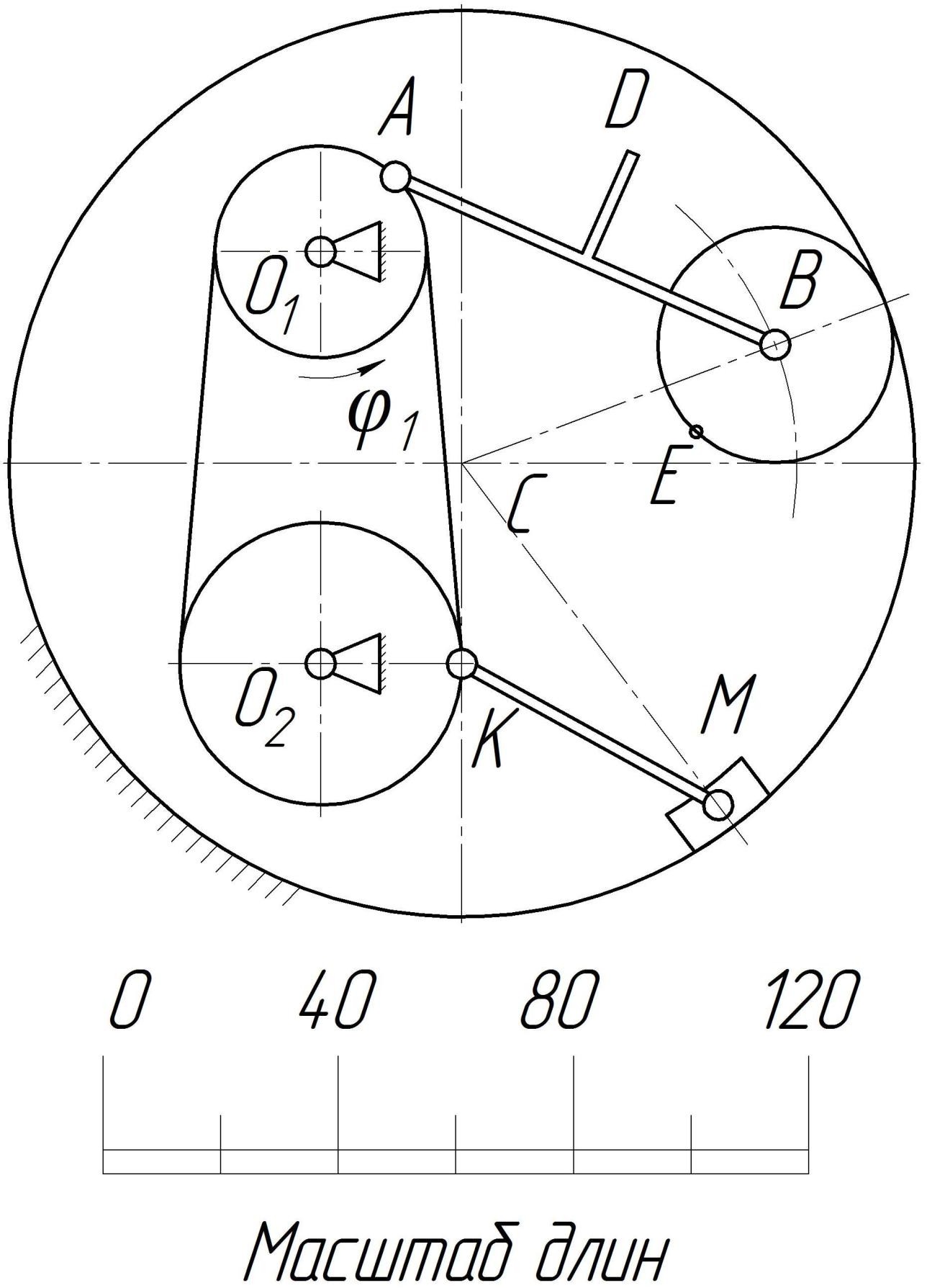

Рис. 5. Вариант плоского многозвенного механизма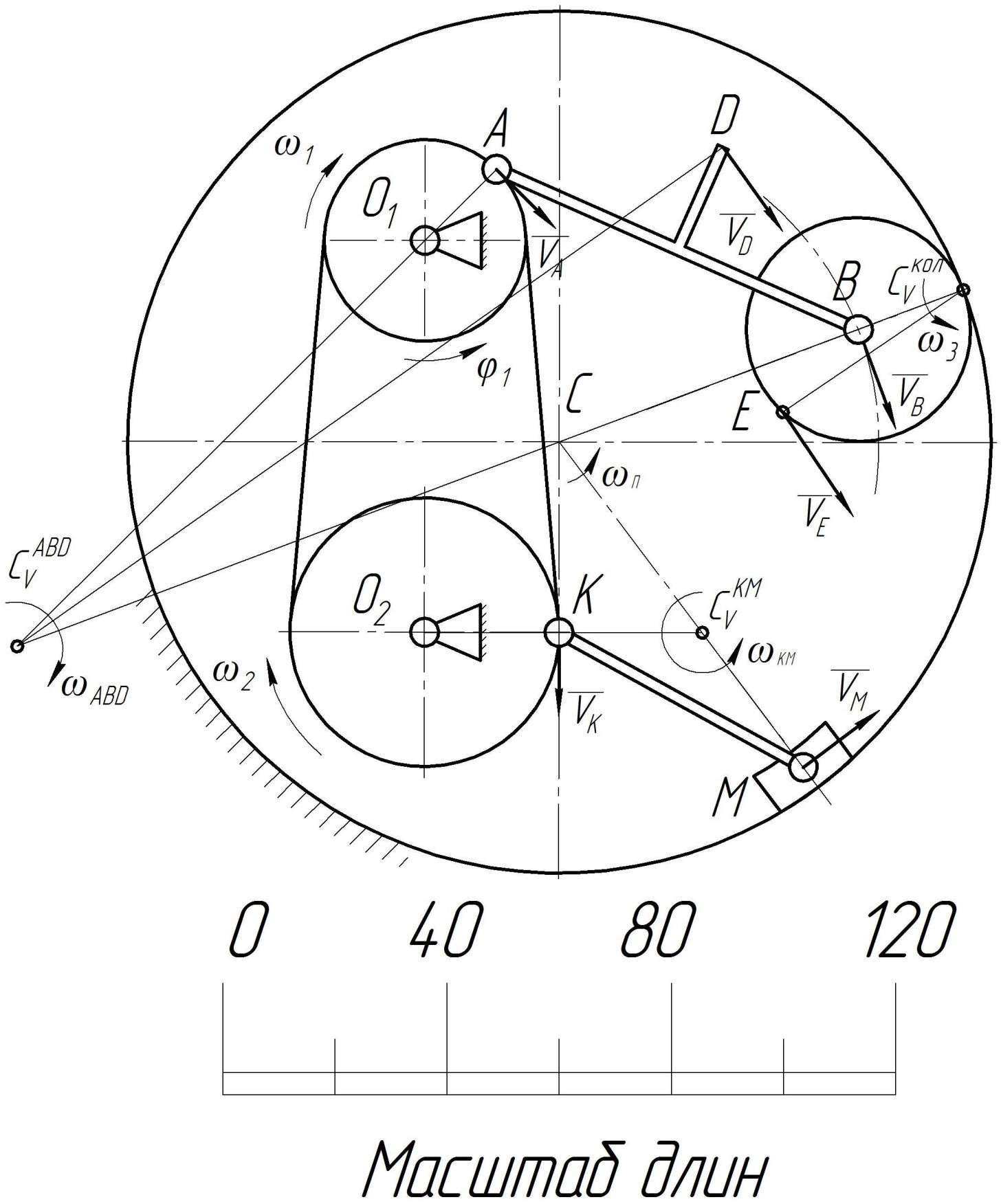



Рис. 6. К определению скоростей точек и угловых скоростей звеньев механизма

Зная величину и направление угловой скорости

ω₁ находим ве-

личину и направление скорости точки А на ободе ведущего колеса. Радиус окружности О₁А по которой движется точка А измеряем с точ- ностью до 1 мм на кинематической схеме механизма (рис. 6) О₁А = 18 мм. С учетом масштаба 1:10 истинный размер О₁А = 18 см = 0,18 м. Отрицательный знак угловой скорости ω₁ уже учтен при определении направления ω₁, поэтому вычисляем модуль скорости точки А:

V_A ω₁  O₁A 3 0,18  0,54

м/с,

но вектор V_A

направляем перпендикулярно радиусу О₁А в сторону,

соответствующую направлению

ω₁.

C
Кроме ведущего колеса точка А принадлежит ещё звену ABD, совершающему плоскопараллельное движение. В заданном положе- нии механизма (в данный момент времени) движение звена ABD можно представить как мгновенно вращательное вокруг оси, прохо-

дящей через мгновенный центр скоростей

ABD V

этого звена перпен-

дикулярно плоскости рисунка. Для определения положения точки

C
ABD V

необходимо знать кроме направления вектора

V_A ещё линию,

вдоль которой направлен вектор скорости другой точки звена ABD. Точка B звена ABD принадлежит ещё и третьему колесу, которое ка- тится по неподвижной цилиндрической поверхности корпуса. Поэто- му траекторией точки В является окружность радиусом СВ. Тогда вектор скорости точки В должен быть направлен по касательной к этой окружности, то есть перпендикулярно радиусу СВ.

Находим положение мгновенного центра скоростей звена ABD.

Для этого из точки А проводим перпендикуляр к вектору V_A

и из точ-

ки В перпендикуляр к линии, вдоль которой направлен вектор скоро- сти точки В. На пересечении этих перпендикуляров находим точку


V
C ^ABD– мгновенный центр скоростей звена ABD.

В соответствии с направлением вектора V_A

направляем угловую

C
скорость звена ω_ABDпри его повороте вокруг оси

ABD V

по часовой

стрелке. Вектор скорости точки В V_B

направляем уже в соответствии

с направлением

ω_ABD . Замеряем на схеме (рис. 6) расстояние от точки

C
А до мгновенного центра скоростей

ABD V

(мгновенный радиус) с уче-

том масштаба

AC ^ABD 120

см = 1,2 м и находим величину угловой

V
скорости звена ABD:

ω
_ V_A
 0,54

 0,45
_с-1_.

V
ABD _ACABD

1,2

C
Соединяем точку D с мгновенным центром скоростей

ABD V

и
направляем вектор скорости V_D

из точки D перпендикулярно мгно-

V
венному радиусу DC ^ABD

в сторону, соответствующую направлению

^ωABD ^.

Замеряем мгновенные радиусы
BC ^ABD 160
см = 1,6 м,

V

V
DC ^ABD 154

см=1,54 м и находим величины скоростей точек В и D,

пропорциональные этим расстояниям:


V
V_B  ω_ABD  BC ^ABD 0,45 1,6  0,72


V
V_D ω_ABD DC^ABD 0,45 1,54  0,69
м/с; м/с.

Третье колесо с подвижной осью В совершает плоскопараллель-

ное движение. Мгновенный центр скоростей колеса

кол


C
V

находится в

точке касания его с неподвижной поверхностью корпуса, так как из условия колесо катится по этой поверхности без проскальзывания. Учитывая свойства мгновенного центра скоростей записываем соот- ношение между скоростями точек В, Е и угловой скоростью колеса:

ω₃ 

V_B


V
_BCкол

 ^VE .


V
_ECкол

Замеряем с учетом масштаба мгновенные радиусы

V
BC^кол  20

см = 0,2 м,

EC^кол  38

см = 0,38 м и находим величины

V

V
скорости точки Е и угловой скорости третьего колеса:

V
V_E 

V_B  EC^кол _BCкол

_ 0,72  0,38

0,2

 1,37
м/с;

ω₃ 

V_B


V
_BCкол

_ 0,72

0,2

 3,6

_с-1_.

В соответствии с известным направлением вектора скорости V_B

направляем угловую скорость колеса против хода часовой стрелки, а

вектор скорости V_E

– перпендикулярно мгновенному радиусу ЕС_V

уже в соответствии с направлением

ω₃ .

Так как проскальзывание между нитью и ободами первого и второго колес отсутствует, то точки на ободах колес, как и все точки нити, имеют одинаковые по величине скорости, следовательно:

V_K  V_A  0.54

м/с.

Угловые скорости колес

ω₁ и

ω₂ совпадают по направлению,

поэтому вектор скорости точки К V_K

направляем перпендикулярно

радиусу О₂К в соответствии с направлением угловой скорости ω₂

второго колеса, которому точка К принадлежит. С учетом масштаба замеряем О₂К = 2,4 см = 0,24 м и находим:

ω₂ 

V_K O₂K

_ 0,54

0,24

 2,25

_с-1_.

Вектор скорости точки МV_M

направляем перпендикулярно ра-

С
диусу СМ окружности, по которой движется точка вместе с ползуном.

Мгновенный центр скоростей

^KM звена КМ находим на пересече-

V
нии перпендикуляров, восстановленных из точек К и М к векторам их

С
скоростей. Угловую скорость

^ωKM

звена КМ при его мгновенном по-

вороте вокруг оси

^KM направляем против часовой стрелки в соот-

V
ветствие с направлением вектора

V_K , а вектор

V_М , перпендикуляр-

ный радиусу СМ и мгновенному радиусу

МС ^KM,

– в сторону, соот-

V

V
ветствующую направлению

^ωKM ^.

Замеряем с учетом масштаба

_KCKM

 26

см = 0,26 м,

V
_MCKM

тельно:

 30

см = 0,3 м, СМ = 73 см = 0,73 м. Вычисляем последова-

ω  ^VK

_ 0,54

 2,01

_с-1_;

V
KM _KCKM



V
0,26

V_М  ω_KM

 MC^KM

 2,01 0,3  0,6 м/с;

и угловую скорость ползуна:

V_M
ω_П  <sub>CM

</sub> 0,6

0,73

 0.82

_с-1_.

Определение ускорений точек и углового ускорения звена

ABD

Вновь строим кинематическую схему механизма в заданном по- ложении в масштабе 1:10 (рис. 7). В соответствии с принятым поло- жительным направлением отсчета угла поворота φ₁ и положительным знаком заданной величины углового ускорения ведущего колеса на- правляем ε₁ против хода часовой стрелки.

Ускорение точки А на ободе ведущего колеса находим по фор- муле сложения ускорений при вращательном движении тела:


A

A

W
W_A  W ^τ  Wⁿ. (6)

Вектор

^τ тангенциальной (касательной) составляющей абсо-

A
лютного ускорения точки А направляем перпендикулярно радиусу окружности О₁А, по которой движется точка А, в соответствие с на-

правлением углового ускорения

ε₁. Величину тангенциальной состав-

ляющей ускорения точки А находим по формуле:

W ^τ  ε  O A  5 0,18  0,9 м/с².


W
A 1 1

Вектор

ⁿ нормальной составляющей ускорения точки А на-

A
правляем по радиусу окружности от точки А к оси вращения, а мо- дуль этой составляющей ускорения:

W ⁿ ω²  O A  3²  0,18  1,62 м/с².

A 1 1

Находим модуль абсолютного ускорения точки А:

W_A 

   1,85

м/с².

Приступаем к определению ускорения точки В звена ABD, тра- ектория которой известна, в отличие от траектории точки D. Выбира- ем за полюс точку А и записываем для точки В векторную формулу сложения ускорений при плоскопараллельном движении звена ABD:

W_B  W_AW_BA. (7)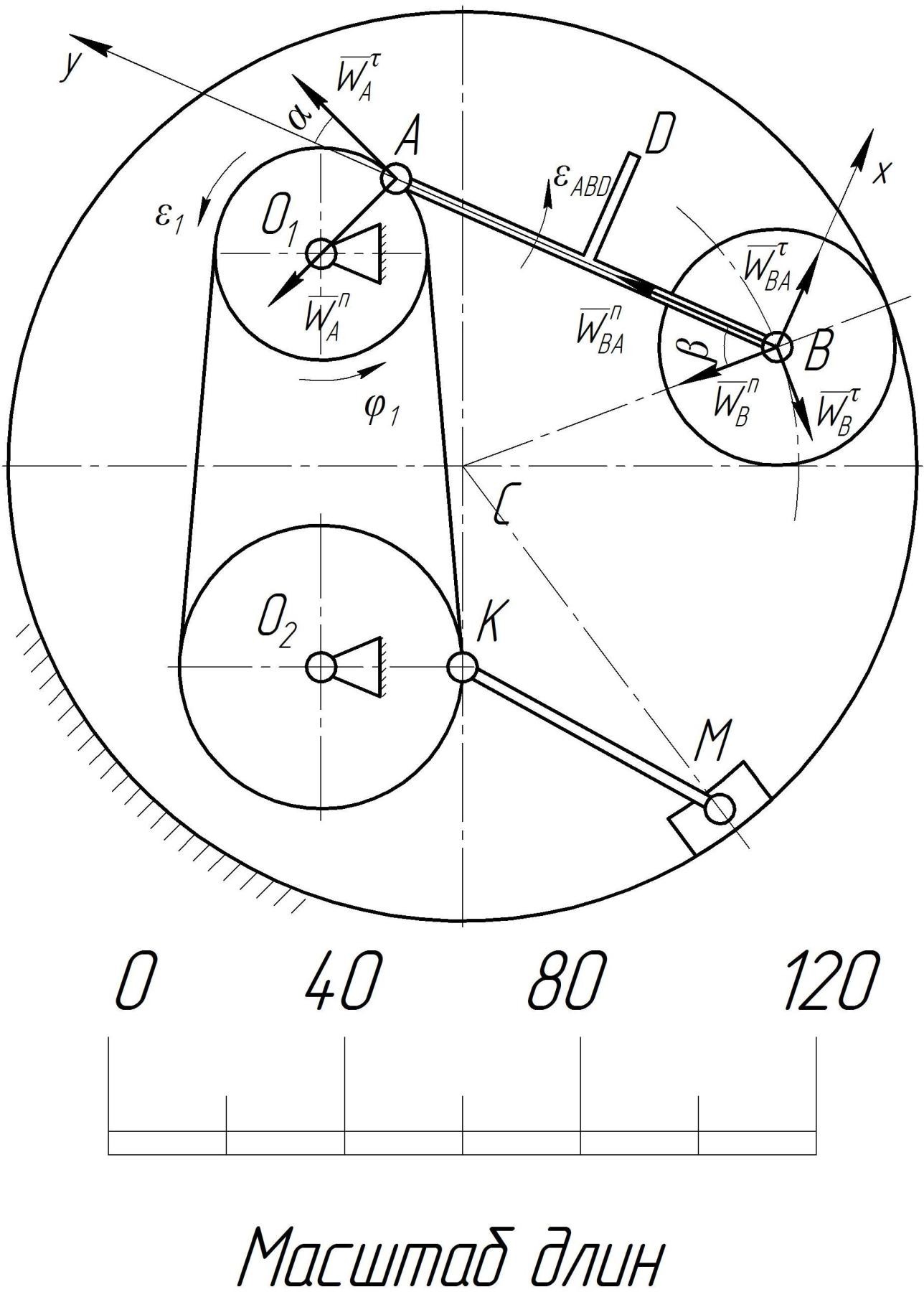

Рис. 7. К определению ускорений точек А и В и углового ускорения звена

Аналитическое определение ускорения точки В сводится к по- следовательному проектированию векторного равенства (7) на оси х, у условно неподвижной системы отсчета.

Для этого сначала определяем направления всех входящих в ра- венство векторов ускорений или их составляющих. Кроме звена ABD точка В находится на оси колеса, которое катится по цилиндрической поверхности неподвижного корпуса. Поэтому траекторией точки В является окружность радиусом СВ и, как следствие:


W

B

B
W_B  W ^τ Wⁿ. (8)




Вектор тангенциальной составляющей ускорения точки В ^τ


B
при движении точки по окружности направляем перпендикулярно ра-




диусу СВв любую сторону. Вектор нормальной составляющей ⁿ


W

B
направляем по радиусу из точки В к точке С.

Вектор ускорения точки В при вращении вокруг условно непод- вижного полюса А, также раскладываем на составляющие:

BA

 W

BA
W_BA  W^{τ n}

(9)

Вектор тангенциальной составляющей W ^τ

направляем из точки

BA
В перпендикулярно АВ в любую сторону, так как направление углово-

го ускорения звена ABD

^ε ABD

пока неизвестно. Вектор нормальной

составляющей W ⁿ

направляем по АВ от точки В к полюсу А.

BA
Подставляя (6), (8) и (9) в (7) получаем векторное равенство:

W ^τ W ⁿ W ^τ W ⁿW ^τ Wⁿ

(10)

B B A A BA BA

где направления всех составляющих векторов известны. Выбираем оси х, у условно неподвижной системы отсчета и после последова- тельного проектирования векторного равенства (10) на эти оси полу- чаем два скалярных уравнения, в которых известны лишь величины

A

A

W
^τ и W ⁿ:

W^ cos Wⁿsin   W^ sin  Wⁿcos   W^ ;

(11)

В В А А ВА

W^ sin   Wⁿcos  W^ cos   Wⁿsin   Wⁿ.

(12)

В В А А ВА

Так как уравнения (11), (12) позволяют найти только две неиз- вестные величины, поэтому предварительно находим величины нор-

мальных составляющих ускорений

n n


W

и

W
B BA

, с учетом найденных в

предыдущем пункте V_B

 0,72

м/с и

ω_ABD  0,45

_с-1_:

_{n V}2

0,72² ₂

W_B ^B

OB

0,57

 0,91

м/с ;

 ω

W
n 2

BA ABD

 AB 0,45²  0,7  0,14

м/с².

Замеряем на схеме механизма (рис. 7) необходимые линейные и угловые размеры AB = 70 см = 0,7 м; OB = 57 см = 0,57 м; α = 22˚; β=45˚, находим sinα=0,37; cosα=0,93; sinβ=0,71; cosβ=0,71 и остав- шиеся неизвестные величины тангенциальных составляющих ускоре- ний.

Из уравнения (12):


^τ B B A BA

W
W ⁿcosβ  W ^τ cos α W ⁿsin α W ⁿ

_B  

sin β

_ 0,91 0,71  0,9  0,93 1,62  0,37  0,14

0,71

 1,31

м/с²;

из уравнения (11)

W^τ  W^τ cosβ Wⁿsinβ W^τ sin α  Wⁿcos α 

BA B B A A

 (1,31)  0,71  0,91 0,71  0,9  0,37 1,62  0,93  1,46 м/с²;

Знаки величин

τ τ


W

и

W
B BA

свидетельствуют о том, что на рис. 7

показано истинное направление вектора

^τ и направление вектора

BA

B

W

W
^τ противоположное действительному.

Модуль абсолютного ускорения точки В:

W_B 

 1,24

м/с².

Учитывая, вместе с тем, известную зависимость W <sup>τ

 ε</sup> ABD

 AB

BA
находим угловое ускорение звена ABD:

_W τ

_{ε ABD }BA

AB

_ 1,46

0,7

 2,09

_с-2_.

Направляем угловое ускорение

^ε ABD

против хода часовой

BA


стрелки в соответствие с направлением вектора W ^τ .