Идз. Вариант 1 1
 Скачать 2.01 Mb. Скачать 2.01 Mb.
|
Вариант № 11№ 1. Для данного повторного интеграла написать уравнения кривых, ограничивающих области интегрирования, вычертить эти области и поменять порядок интегрирования: 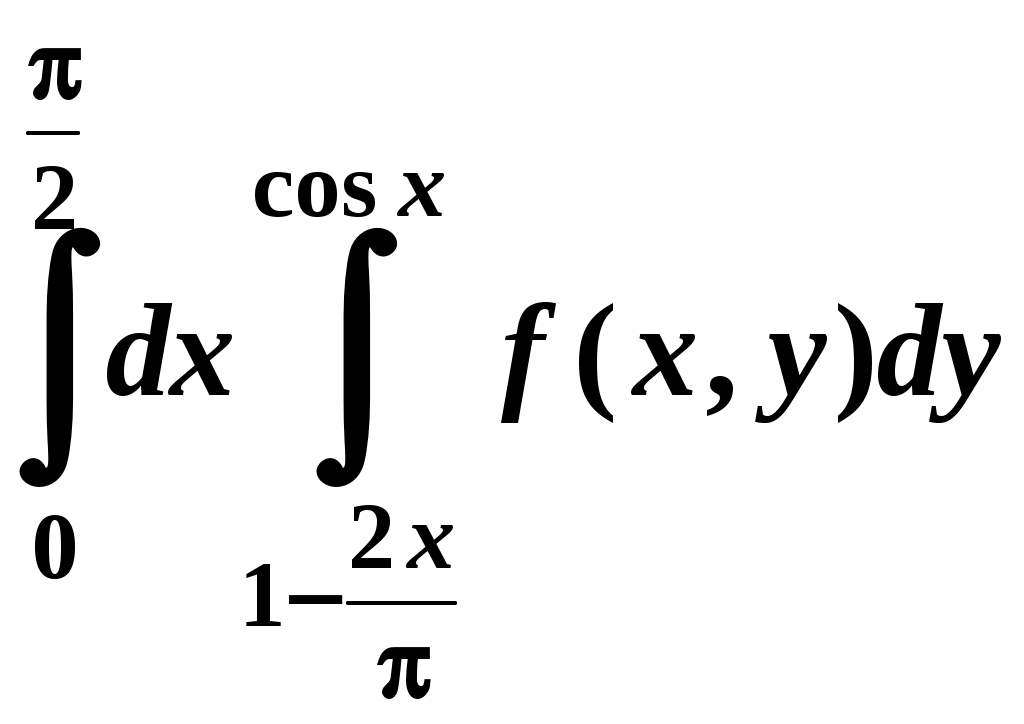 . .№ 2. Расставить пределы интегрирования в том и другом порядке в двойном интеграле 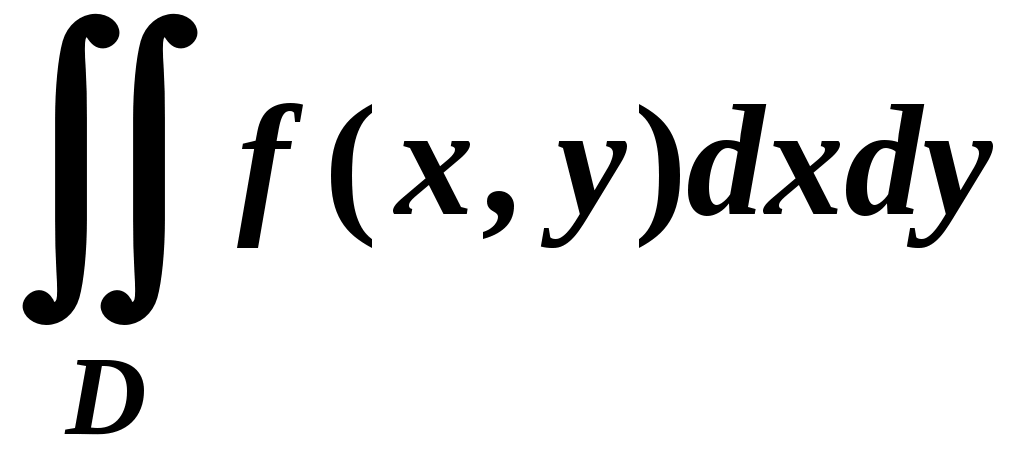 , если D – параллелограмм A(–1, –2), B(–1, 2),C(1, 4),D(1, 0). , если D – параллелограмм A(–1, –2), B(–1, 2),C(1, 4),D(1, 0).№ 3. Вычислить массу пластины D с поверхностной плотностью D : треугольник A(0, –1), B(0, 2),C(3, –1). № 4. Вычислить двойной интеграл по области D, ограниченной линиями: 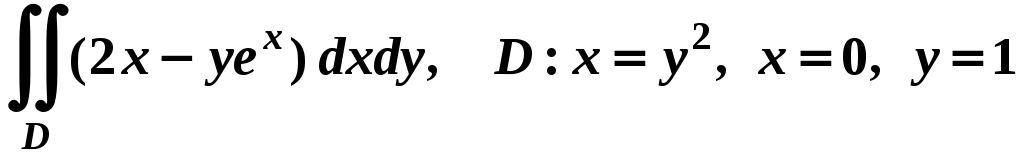 . .№ 5. Переходя к полярным координатам вычислить интеграл по области D, ограниченной заданными линиями: 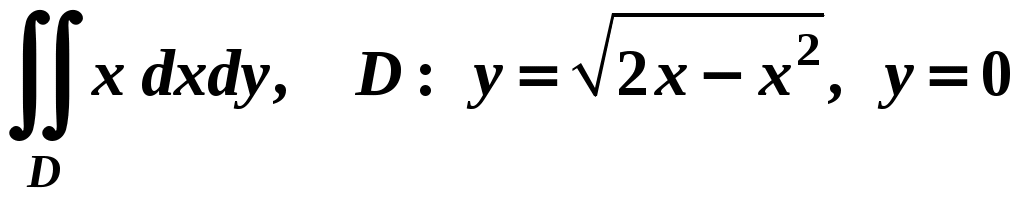 . .№ 6. Найти площадь фигуры, ограниченной линиями: № 7. Найти координаты центра тяжести однородной плоской фигуры, ограниченной линиями: № 8. С помощью двойного интеграла вычислить объём тела, ограниченного поверхностями: параболоид № 9. Для данного интеграла написать уравнения поверхностей, ограничивающих область интегрирования, и вычертить эту область: 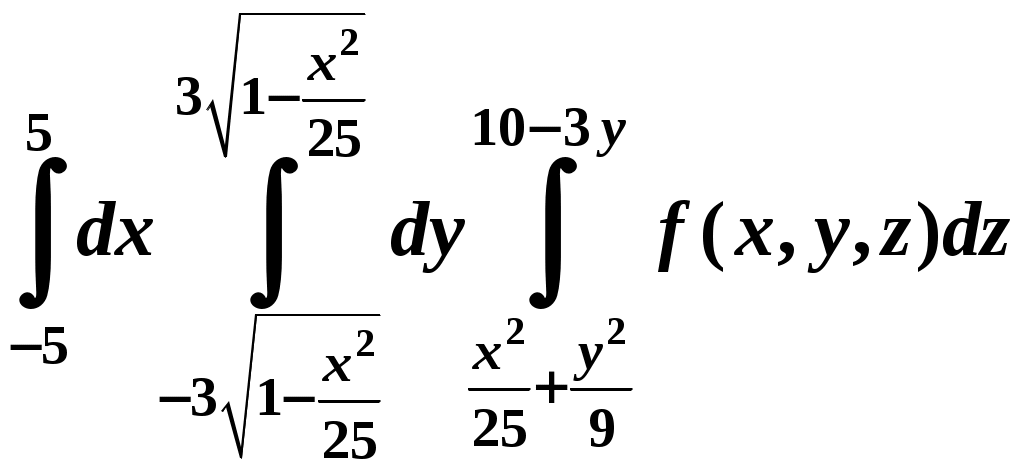 . .№ 10. Вычислить 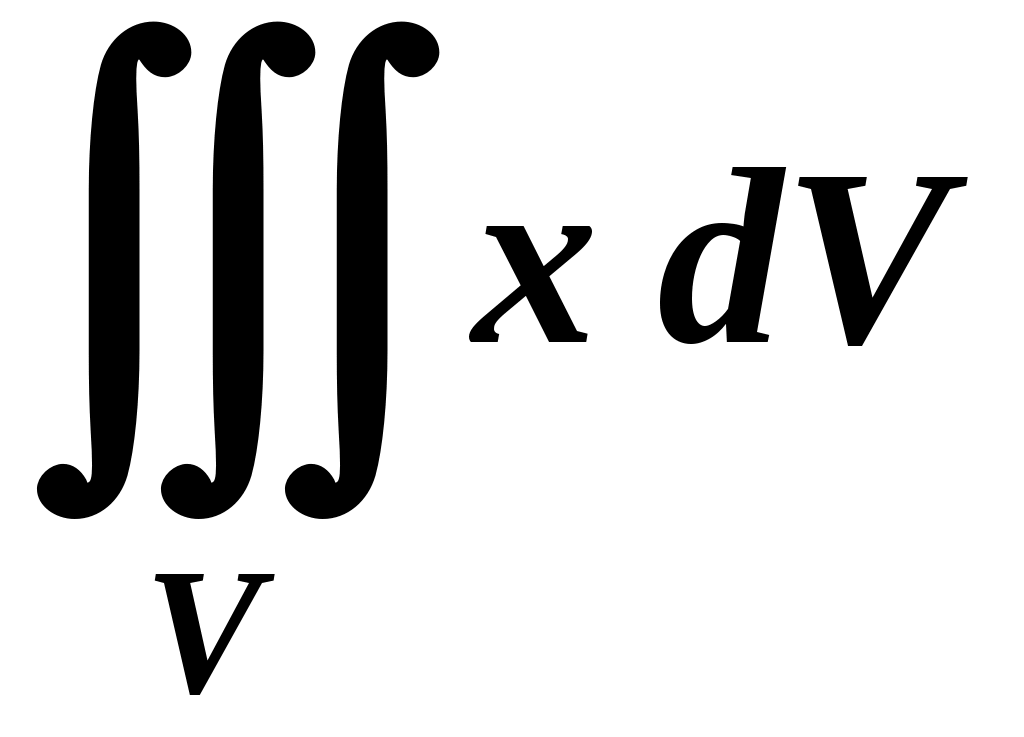 , если , если 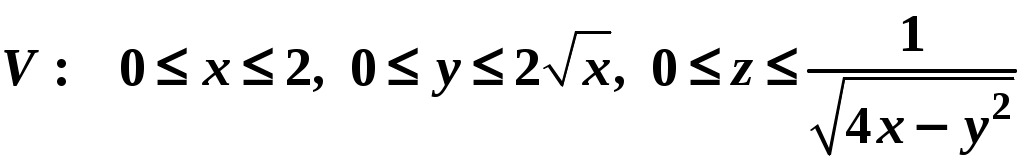 . .№ 11. Вычислить 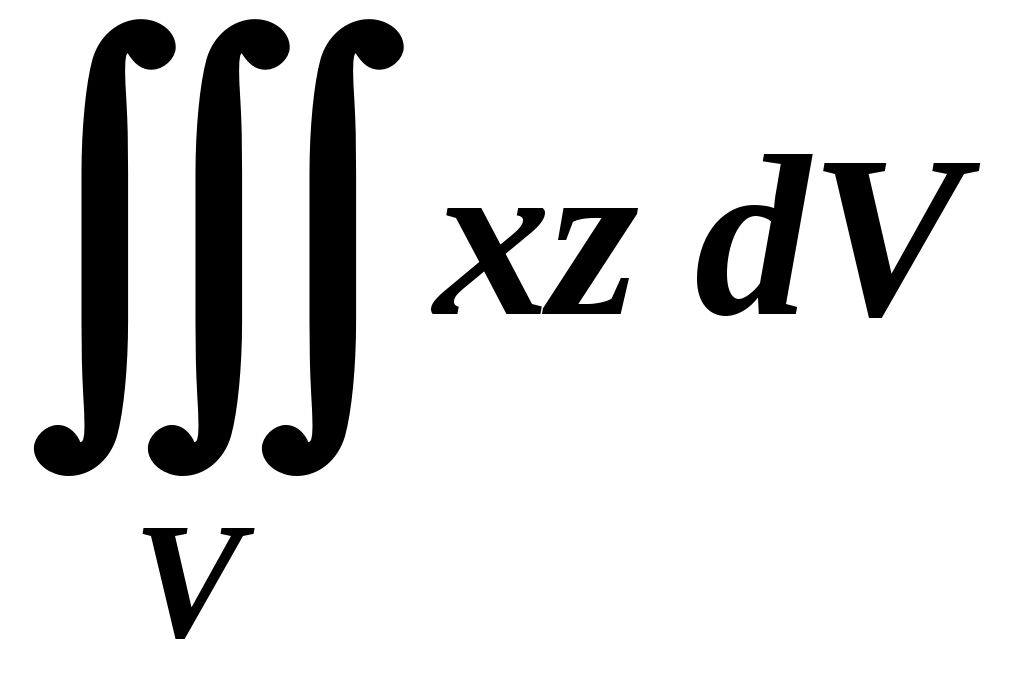 , сведением к однократному и двойному интегралам: , сведением к однократному и двойному интегралам: № 12. Вычислить тройной интеграл 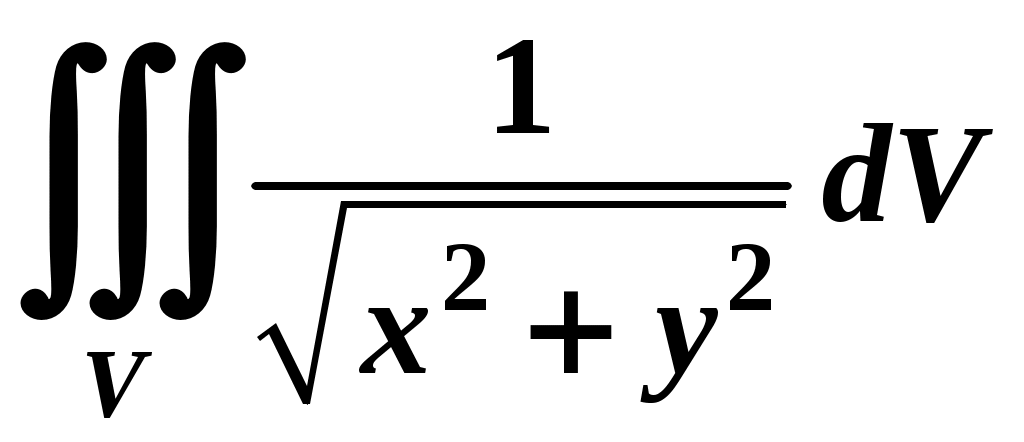 , перейдя к цилиндрическим координатам: , перейдя к цилиндрическим координатам: № 13. Вычислить тройной интеграл 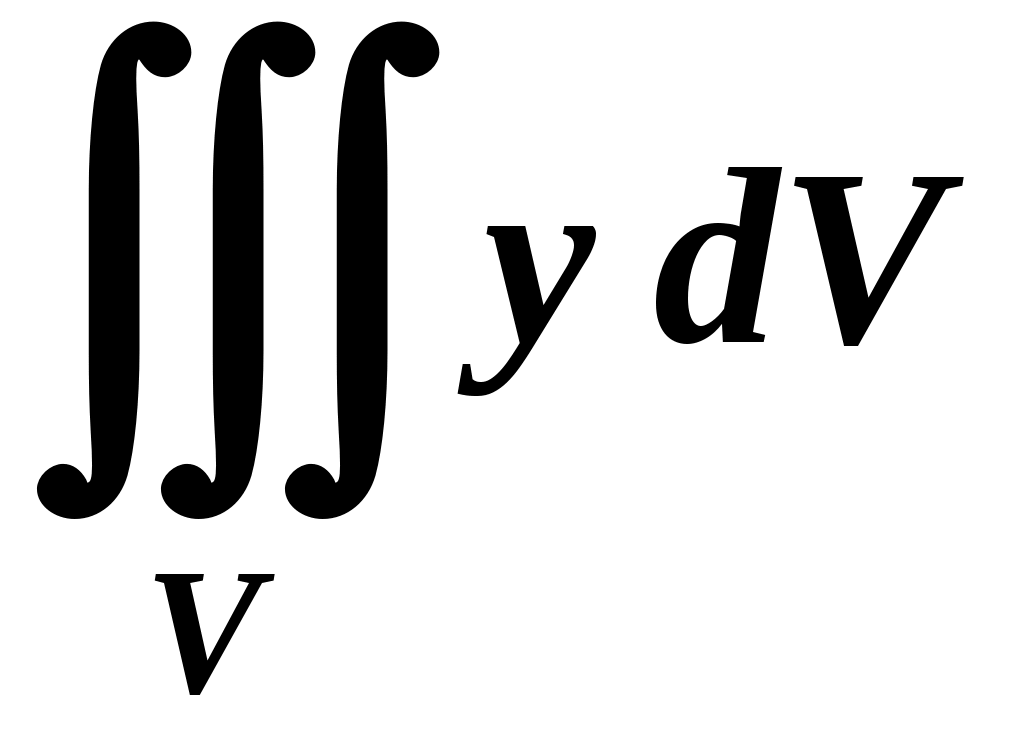 , перейдя к сферическим координатам: , перейдя к сферическим координатам: № 14. Приложения тройного интеграла в геометрии. Найти объём тела, ограниченного заданными поверхностями: № 15. Вычислить криволинейный интеграл 1-го рода по ломаной ABC: № 16. Вычислить криволинейный интеграл 1-го рода: 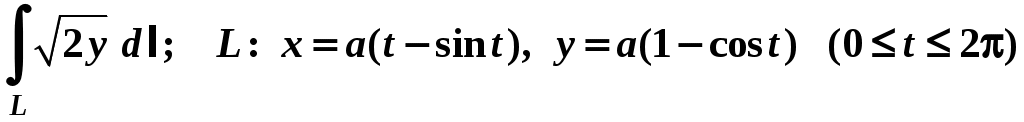 . .№ 17. Вычислить криволинейный интеграл второго рода 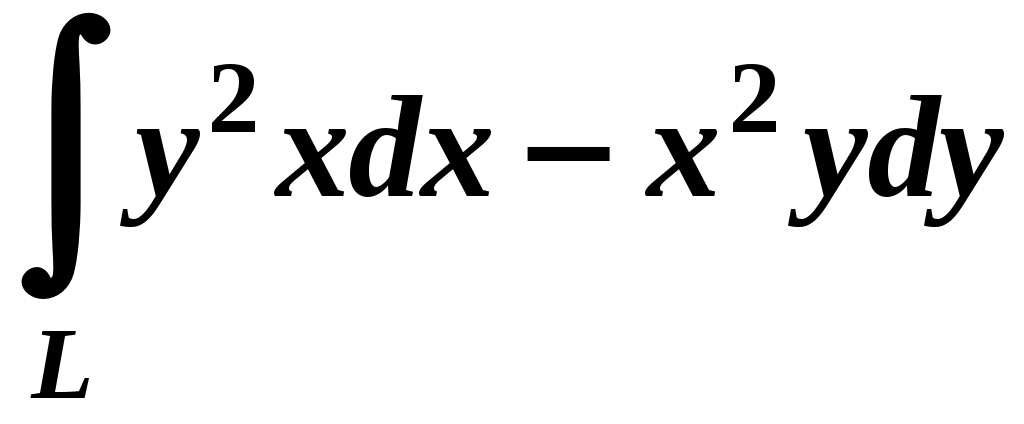 по кривой по кривой № 18. Вычислить криволинейный интеграл второго рода 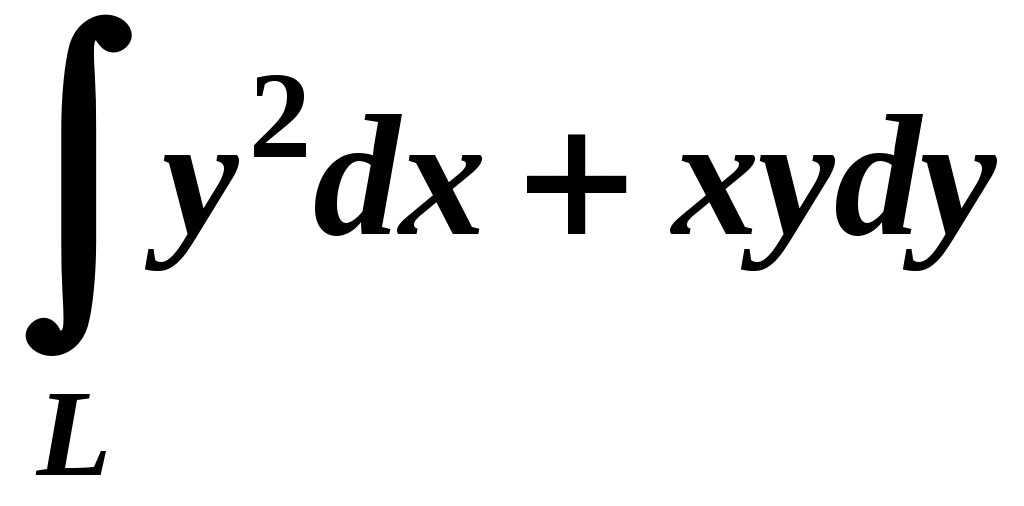 по линии по линии № 19. Найти массу материальной дуги 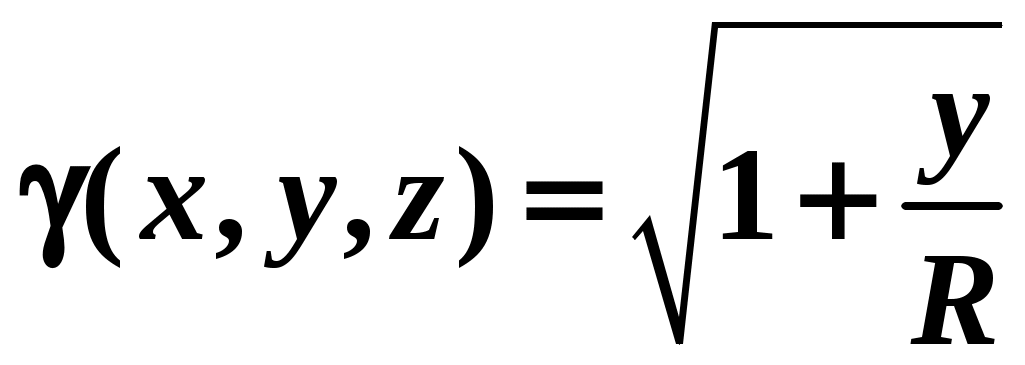 . .№ 20. Вычислить криволинейный интеграл 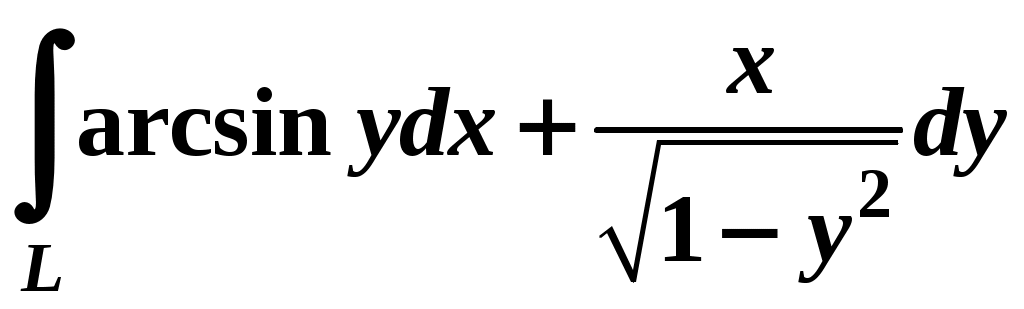 между точками A(0, 0) и B между точками A(0, 0) и B№ 21. Вычислить криволинейный интеграл 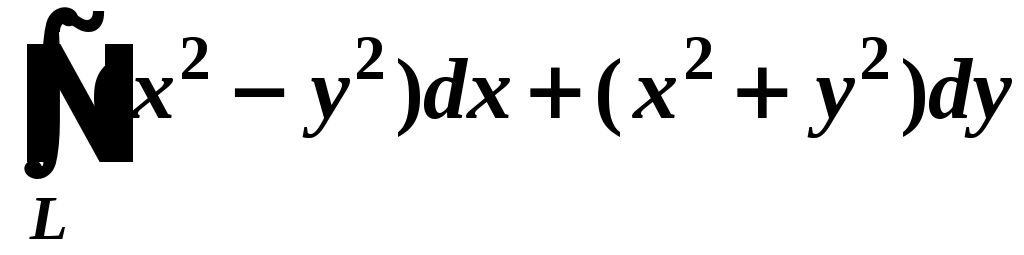 , применив формулу Грина (обход контура L : контур, образованный осью OX и полуокружностью , применив формулу Грина (обход контура L : контур, образованный осью OX и полуокружностью ТИПОВОЙ РАСЧЁТ (ДВОЙНЫЕ, ТРОЙНЫЕ И КРИВОЛИНЕЙНЫЕ ИНТЕГРАЛЫ) |
