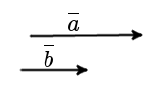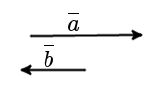Векторы на плоскости и в пространстве. Векторы на плоскости и в пространстве. Действия над векторами
 Скачать 1.27 Mb. Скачать 1.27 Mb.
|
|
Векторы на плоскости и в пространстве. Действия над векторами. Понятие вектора является одним из наиболее основных в математике, объединяющим такие ее разделы, как геометрия, алгебра, математический анализ. Оно имеет большое прикладное значение, так как многие физические величины (сила, скорость и другие) характеризуются не только величиной, но и направлением, то есть являются векторными величинами. При изучении электрических и магнитных явлений появляются новые примеры векторных величин (векторы напряженности электрического поля, вектор магнитной индукции). 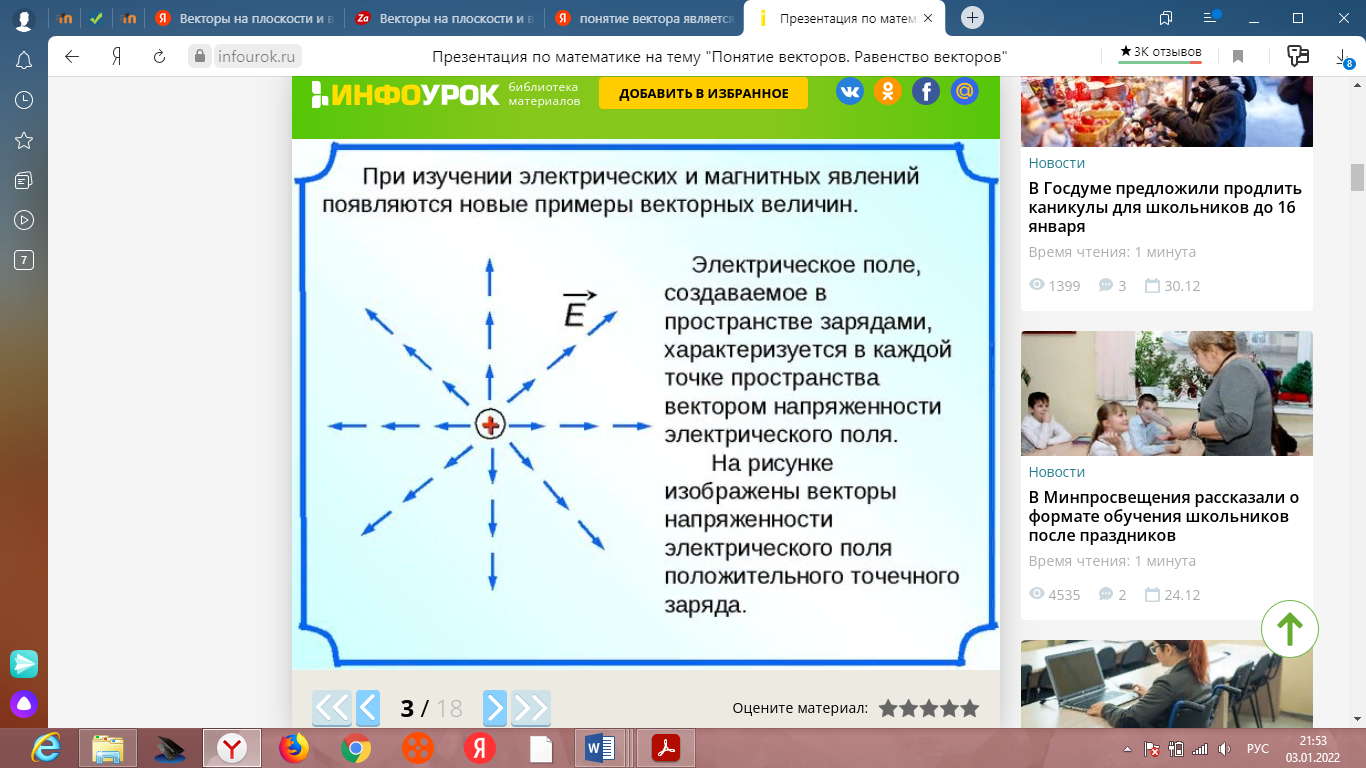 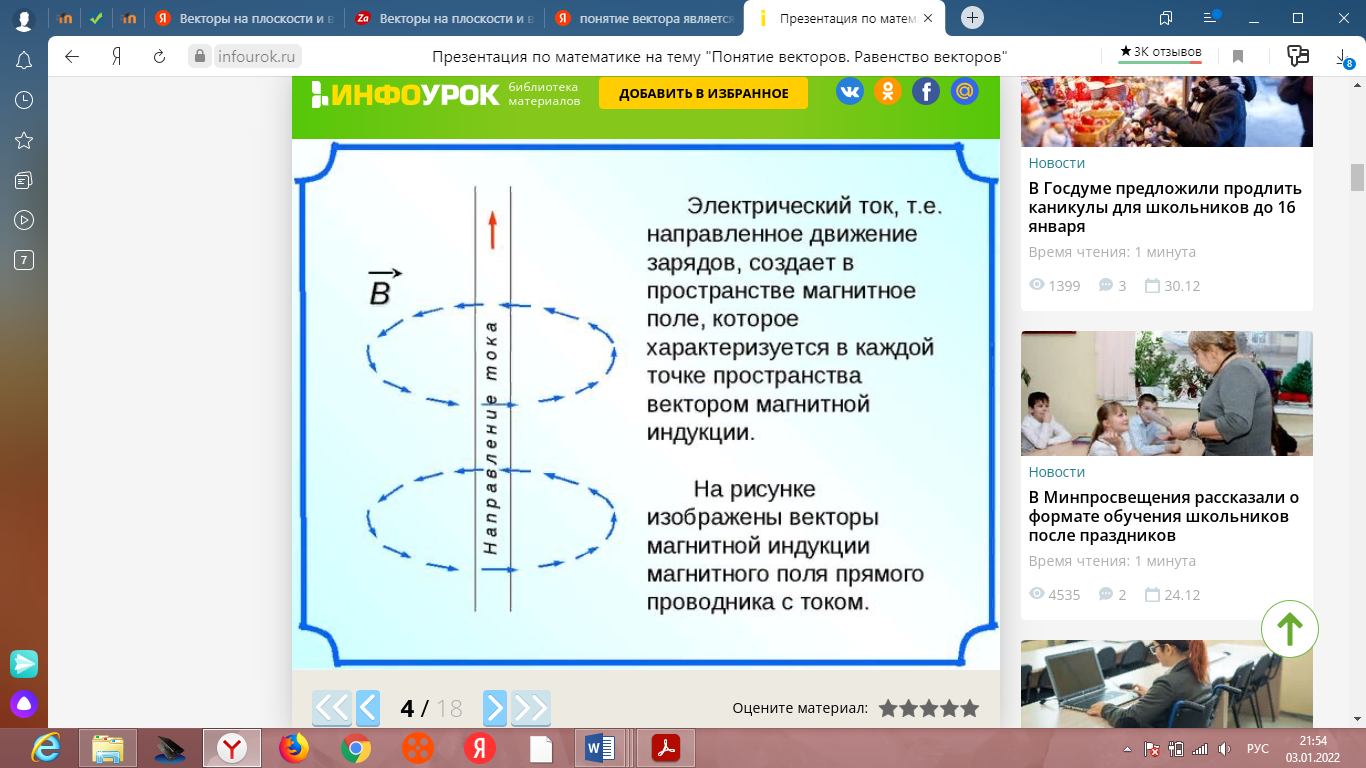 В планиметрии мы изучали векторы на плоскости. Вспомним некоторые определения и свойства векторов. Решение задач. 1. В прямоугольнике АВСD АВ=3см, ВС=4см, точка М – середина стороны АВ. Найдите длины векторов. 2. АВСD – прямоугольная трапеция. Боковая сторона АВ = 5 см, большее основание AD = 12 см, угол при основании равен 45°. Найти длины векторов Здесь мы рассмотрим векторы в пространстве. Их определение и свойства аналогичны определению и свойствам векторов на плоскости. Вектор - это отрезок, который имеет направление. Конец вектора совпадает со стрелкой, начало - точка. Длина или модуль вектора (абсолютная величина) - длина этого направленного отрезка. Для обозначения длины вектора используются две вертикальные линии слева и справа |AB|. Нулевым вектором называется вектор, у которого начальная и конечная точка совпадают. Нулевой вектор обычно обозначается как 0. Длина нулевого вектора равна нулю. Два ненулевых вектора называются коллинеарными, если они лежат на одной прямой или на параллельных прямых.
Условия коллинеарности векторов Два вектора будут коллинеарны при выполнении любого из этих условий: 1. Два вектора a и b коллинеарны, если существует число n такое, что a = n · b 2. Два вектора коллинеарны, если отношения их координат равны. N.B. Условие 2 неприменимо, если один из компонентов вектора равен нулю. 3. Два вектора коллинеарны, если их векторное произведение равно нулевому вектору. N.B. Условие 3 применимо только для трехмерных (пространственных) задач. Векторное произведение вычисляется по формуле: 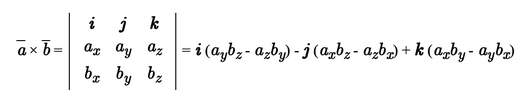 Пример 1. Какие из векторов 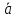 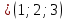 , , 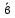 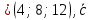 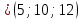 коллинеарные? коллинеарные?Воспользуемся вторым условием:  . . Значит: 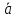 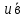 коллинеарные т.к. коллинеарные т.к. 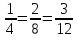 . .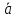 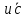 не коллинеарные т.к. не коллинеарные т.к. 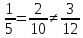 . .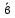 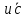 не коллинеарные т.к. не коллинеарные т.к. 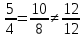 . .Пример 2. Доказать, что вектора 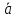 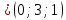 , , 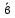 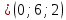 коллинеарные. коллинеарные. Так как вектора содержат компоненты равные нулю, то воспользуемся первым условием:  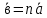 . для этого найдем ненулевой компонент вектора . для этого найдем ненулевой компонент вектора 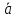 в данном случае это в данном случае это 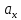 . если вектора коллинеарные, то n= . если вектора коллинеарные, то n=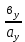 = =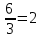 . Найдем . Найдем 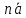 . . 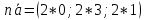 = =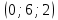 . Так как . Так как 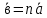 , то векторы , то векторы 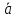 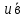 коллинеарные. коллинеарные.Пример 3. Найти значение параметров n и m при которых вектора 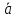 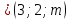 , , 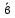 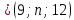 . . Ответ: вектора a и b коллинеарны при n = 6 и m = 4. Два коллинеарных вектора a и b называются сонаправленными векторами, если их направления совпадают: a↑↑b
Два коллинеарных вектора a и b называются противоположно направленными векторами, если их направления противоположны: a↑↓b
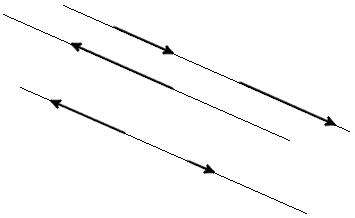
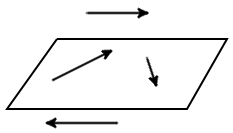
Вектора, параллельные одной плоскости или лежащие на одной плоскости называют компланарными векторами.
Всегда возможно найти плоскости параллельную двум произвольным векторам, по этому любые два вектора всегда компланарные. Условия компланарности векторов Для 3-х векторов. Три вектора компланарны если их смешанное произведение равно нулю. Для 3-х векторов. Три вектора компланарны если они линейно зависимы. Пример Доказать, что три вектора 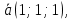 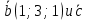 (2;2;2) компланарны. Решение: найдем смешанное произведение векторов используя матрицу (2;2;2) компланарны. Решение: найдем смешанное произведение векторов используя матрицу 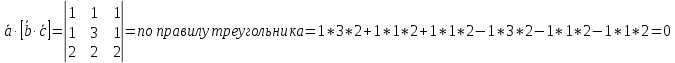 . Следовательно вектора компланарны так, как их смешанное произведение равно нулю. . Следовательно вектора компланарны так, как их смешанное произведение равно нулю.Вектора a и b называются равными, если они лежат на одной или параллельных прямых, их направления совпадают, а длины равны
Условие равенства векторов. Вектора равны, если их координаты равны. То есть, два вектора равны, если они коллинеарные, сонаправленые и имеют равные длины: a = b, если a↑↑b и |a| = |b|. Пример 1. Определить какие из векторов равны 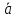 = {1; 2; 4}, = {1; 2; 4}, 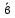 = {1; 2; 2}, = {1; 2; 2}, 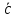 = {1; 2; 4}. = {1; 2; 4}.Решение: 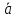 = =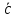 - так как их координаты равны, - так как их координаты равны,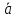 ≠ ≠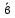 - так как их координаты не равны, - так как их координаты не равны,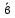 ≠ ≠ 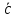 - так как их координаты не равны. - так как их координаты не равны.Пример 2. При каком значении параметра n вектора 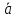 = {1; 2; 4} и = {1; 2; 4} и 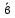 = {1; 2; 2n} равны. = {1; 2; 2n} равны.Решение: Проверим равенство компонентов векторов ax = bx = 1 ay = by = 2 az = bz => 4 = 2n => n = 4/2 = 2 Ответ: при n = 2 вектора 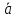 и и  равны. равны.Решение задач 1.Дано: ABCD – тетраэдр. Точки M, N, K – середины AC, BC, CD; соответственно, AB=3 см, BC=4 см, BD=5 см. (Рис1) Найти: AB, BC, BD, NM, BN, NK. 2. Дан параллелепипед ABCDA1B1C1D1 Точки M и K – середины рёбер B1C1и A1D1. (Рис 2 )Укажите все пары: а) сонаправленных векторов; б) противоположно направленных векторов; в) равных векторов. 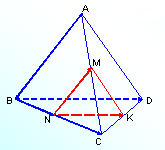 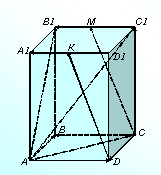 рис 1 рис 2 Действия над векторами. Пусть в трехмерном пространстве заданы векторы 1.Сложение двух векторов производится покоординатно, то есть если Данная формула имеет место для произвольного конечного числа слагаемых. Геометрически два вектора складываются по двум правилам: а) правилотреугольника– результирующий вектор суммы двух векторов соединяет начало первого из них с концом второго при условии, что начало второго совпадает с концом первого вектора; для суммы векторов – результирующий вектор суммы соединяет начало первого из них с концом последнего вектора-слагаемого при условии, что начало последующего слагаемого совпадает с концом предыдущего; б) правилопараллелограмма (для двух векторов) – параллелограмм строится на векторах-слагаемых как на сторонах, приведенных к одному началу; диагональ параллелограмма исходящая из их общего начала, является суммой векторов. 2.Вычитание двух векторов производится покоординатно, аналогично сложению, то есть если Геометрически два вектора складываются по уже упомянутому правилу параллелограмма с учетом того, что разностью векторов является диагональ, соединяющая концы векторов, причем результирующий вектор направлен из конца вычитаемого в конец уменьшаемого вектора. Важным следствием вычитания векторов является тот факт, что если известны координаты начала и конца вектора, то для вычисления координат вектора необходимо из координат его конца вычесть координаты его начала. Действительно, любой вектор пространства 3. Умножение вектора на число λпокоординатно: При λ>0 – вектор |