64_90_Глава 4 Векторная алгебра. Векторная алгебра
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
Глава 4 Векторная алгебра §1 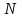 -мерные векторы в линейном пространстве -мерные векторы в линейном пространстве 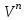 . Линейная зависимость и независимость векторов. Базис. Скалярное произведение векторов . Линейная зависимость и независимость векторов. Базис. Скалярное произведение векторовВектором называется упорядоченный набор из 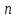 действительных чисел, записываемый в виде действительных чисел, записываемый в виде 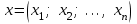 , где , где 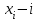 -й элемент (или i-я координата) вектора х. -й элемент (или i-я координата) вектора х.Размерность вектора определяется числом его координат и является его отличительной характеристикой. Например, 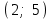 - двумерный вектор, - двумерный вектор, 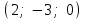 - трехмерный, - трехмерный, 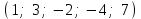 - пятимерный, - пятимерный, 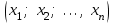 - - 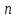 -мерный вектор. -мерный вектор.Векторы равны только в том случае, если они имеют одну и ту же размерность и равные соответствующие координаты. Отсюда следует, что координаты вектора нельзя менять местами: так, 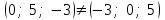 . .Нулевым вектором называется вектор, все координаты которого равны нулю: 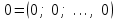 . .Произведением вектора 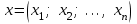 на действительное число на действительное число 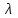 называется вектор называется вектор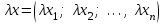 , ,т.е. при умножении вектора на число каждая его координата умножается на это число. Зная вектор 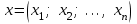 , можно получить противоположный вектор , можно получить противоположный вектор 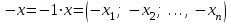 . .Суммой векторов 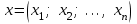 и и 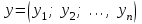 называется вектор называется вектор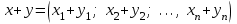 , ,т.е. при сложении векторов одной и той же размерности их соответствующие координаты почленно складываются. Очевидно, что 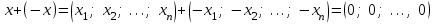 т.е. сумма противоположных векторов дает нулевой вектор. Используя понятие противоположного вектора, можно определить операцию вычитания векторов: 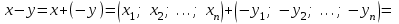 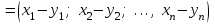 , ,т.е. при вычитании двух векторов одной и той же размерности их соответствующие координаты почленно вычитаются. Нетрудно заметить, что линейные операции над векторами удовлетворяют следующим свойствам: 10 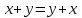 . .20 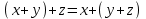 . .30 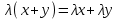 . .40 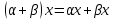 . .50 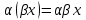 . .60 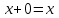 . .70 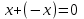 . .80 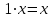 . .Скалярным произведением двух векторов в 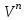 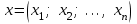 и и 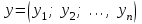 называется число, равное сумме произведений соответствующих координат векторов называется число, равное сумме произведений соответствующих координат векторов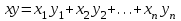 . (11) . (11)Нетрудно проверить, что скалярное произведение векторов обладает следующими свойствами: 10 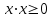 , причем , причем 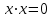 лишь при лишь при 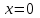 . .20 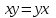 . .30 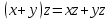 . .40 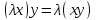 . .Среди скалярных произведений особое место занимает скалярный квадрат: 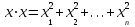 . .Нормой (длиной) вектора в 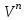 называется число, равное квадратному корню из скалярного произведения вектора самого на себя называется число, равное квадратному корню из скалярного произведения вектора самого на себя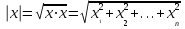 , (12) , (12)Некоторое множество 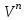 образует линейное пространство, если для любых двух его элементов образует линейное пространство, если для любых двух его элементов 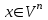 и и 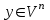 определена операция сложения определена операция сложения 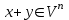 и для каждого элемента и для каждого элемента 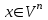 и любого действительного числа и любого действительного числа 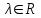 определено произведение определено произведение 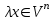 , причем эти операции удовлетворяют свойствам 10 – 80. , причем эти операции удовлетворяют свойствам 10 – 80.Подмножество 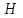 линейного пространства линейного пространства 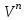 называют линейным подпространством, если выполнены следующие два условия: называют линейным подпространством, если выполнены следующие два условия:сумма любых двух векторов из 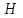 принадлежит принадлежит 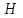 : : 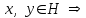 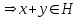 ; ;произведение любого вектора из 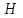 на любое действительное число снова принадлежит на любое действительное число снова принадлежит 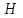 : : 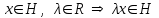 . .Таким образом, множество 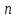 -мерных векторов с действительными координатами образует линейное векторное пространство. -мерных векторов с действительными координатами образует линейное векторное пространство.Линейное пространство называется евклидовым 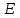 , если в нем определено скалярное произведение, удовлетворяющее свойствам 10 – 40. Так как для , если в нем определено скалярное произведение, удовлетворяющее свойствам 10 – 40. Так как для 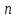 -мерных векторов скалярное произведение определено, то все множество -мерных векторов скалярное произведение определено, то все множество 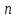 -мерных векторов образует евклидово пространство. -мерных векторов образует евклидово пространство.Линейной комбинацией векторов 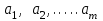 из из 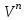 называется сумма вида называется сумма вида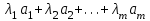 , ,где 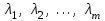 - действительные числа, называемые коэффициентами линейной комбинации. - действительные числа, называемые коэффициентами линейной комбинации.Линейная комбинация векторов является вектором. Система векторов называется линейно зависимой, если их линейная комбинация равна нулевому вектору при хотя бы одном из коэффициентов линейной комбинации отличном от нуля. Т.е. векторы 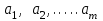 - называются линейно зависимыми, если равенство - называются линейно зависимыми, если равенство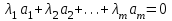 , при , при 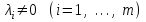 , ,выполняется при хотя бы одном из коэффициентов линейной комбинации, отличном от нуля. Смысл зависимости между векторами ясен из следующей теоремы. Теорема 1 Если система векторов линейно зависима, то хотя бы один из них можно представить в виде линейной комбинации остальных. Теорема 2 (обратная) Если один из векторов данной системы можно представить в виде линейной комбинации остальных, то такая система векторов линейно зависима. Система векторов называется линейно независимой, если их линейная комбинация равна нулевому вектору при всех нулевых коэффициентах линейной комбинации. Иными словами, векторы 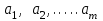 называются линейно независимыми, если равенство называются линейно независимыми, если равенство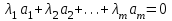 возможно лишь тогда, когда 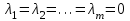 . .Базисом называется упорядоченная система линейно независимых векторов, через которые выражается любой вектор пространства. Теорема 3 Если в векторном пространстве выбран какой-либо базис, то любой вектор этого пространства можно однозначно представить в виде линейной комбинации векторов базиса (такое представление называется разложение вектора по данному базису). Матрицей перехода от старого базиса 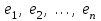 к новому к новому 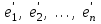 называется матрица называется матрица 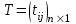 , по столбцам которой стоят координаты новых базисных векторов в старом базисе. Таким образом, старый и новый базисы связаны матричным равенством , по столбцам которой стоят координаты новых базисных векторов в старом базисе. Таким образом, старый и новый базисы связаны матричным равенством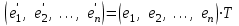 . .При таких обозначениях координаты 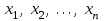 вектора вектора 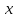 в старом базисе связаны с координатами в старом базисе связаны с координатами  того же вектора в новом базисе равенствами того же вектора в новом базисе равенствами 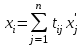 , или в матричной записи , или в матричной записи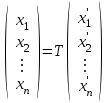 . .Теорема Для любых векторов 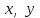 евклидова пространства евклидова пространства 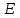 справедливо неравенство Коши-Буняковского справедливо неравенство Коши-Буняковского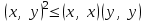 . .Углом 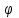 между ненулевыми векторами между ненулевыми векторами 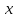 и и 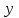 в евклидовом пространстве в евклидовом пространстве 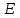 называют значение называют значение 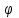 на отрезке от 0 до на отрезке от 0 до 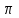 , определяемое равенством , определяемое равенством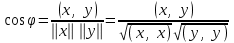 . .Два вектора в евклидовом пространстве называют ортогональными, если их скалярное произведение равно нулю. Теорема (Теорема Пифагора) Если векторы 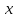 и и 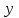 из евклидова пространства ортогональны, то из евклидова пространства ортогональны, то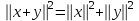 . .Систему векторов евклидова пространства называют ортогональной, если любые два вектора из этой системы ортогональны. Ортогональный базис называют ортонормированным, если каждый вектор этого базиса имеет норму (длину), равную единице. Практическое занятие № 7 Задание 1 Является ли линейно зависимой система векторов: 1) 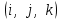 2) 2) 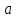 и и 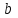 , , 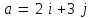 ; ; 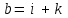 ; ;3) 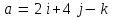 , , 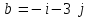 , , 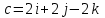 . .Решение. 1) 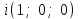 , , 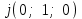 , , 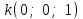 . .Составим линейную комбинацию векторов 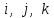 на числа на числа 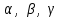 , т.е. , т.е. 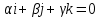 . .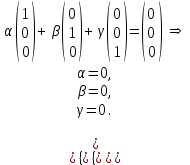 Так как все числа 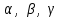 равны 0, то система векторов равны 0, то система векторов 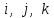 линейно независимая. линейно независимая.2) 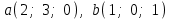 . .Составим линейную комбинацию векторов 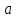 и и 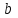 на числа на числа 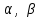 , т.е. , т.е. 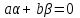 . .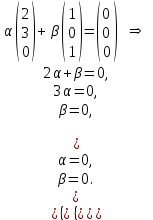 Следовательно, система векторов 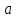 и и 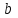 - линейно независимая. - линейно независимая.3) 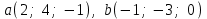 , , 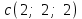 . .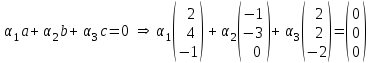 . .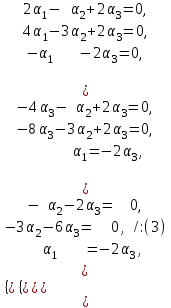 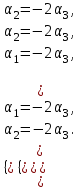 Пусть 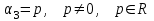 , тогда , тогда 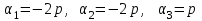 . .Таким образом, мы нашли совокупность чисел, отличных от нуля 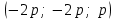 , при которых линейная комбинация будет равна 0 (нулевому вектору), т.е. , при которых линейная комбинация будет равна 0 (нулевому вектору), т.е. 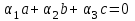 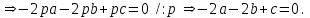 Мы доказали, что векторы  , ,  и и 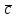 - линейно зависимые. - линейно зависимые. Так как векторы линейно зависимы, то любой вектор можно выразить через остальные векторы. Например, 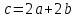 или или 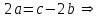 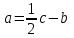 или или 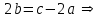 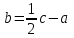 . .Ответ. 1) нет; 2) нет; 3) да. Задача 2 Выяснить, образуют ли базис векторы 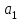 , , 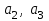 : : 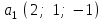 , , 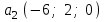 , , 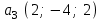 . .Решение. Базисом называется система линейно независимых векторов, через которые можно выразить любой вектор пространства. Докажем, что вектора 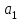 , , 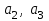 линейно независимые. линейно независимые.Составим линейную комбинацию векторов и найдем числа 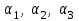 . .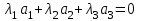 . .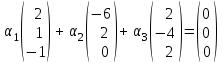 , ,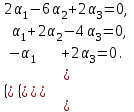 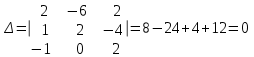 . .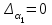 , , 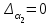 , , 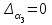 . .Таким образом 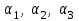 - бесчисленное множество решений, а следовательно, - бесчисленное множество решений, а следовательно, 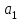 , , 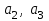 - линейно зависимы, т.е. векторы - линейно зависимы, т.е. векторы 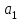 , , 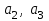 не могут образовывать базис. не могут образовывать базис.Ответ. нет. Задача 3 Найти координаты вектора 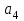 в базисе в базисе 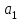 , , 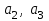 : : 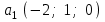 , , 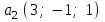 , , 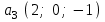 , , 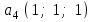 . .Решение. Разложим вектор 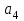 по векторам по векторам 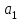 , , 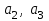 : :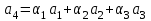 . .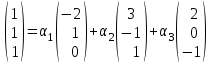 , ,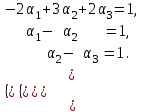 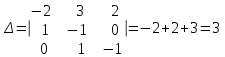 . .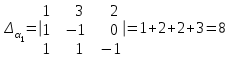 . .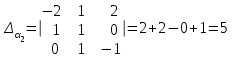 . .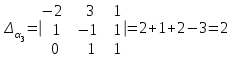 . .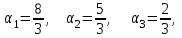 . .Таким образом, 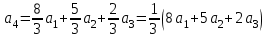 . . Ответ. Да. 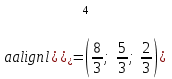 . .Задача 4 Задано линейное пространство 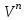 при при 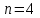 . Определить угол между векторами . Определить угол между векторами 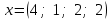 и и 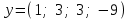 . .Решение. 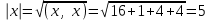 ; ; 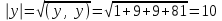 ; ; 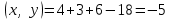 ; ; 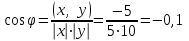 ; ; 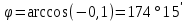 . .Задача 5 Рассматривается евклидово пространство непрерывных функций 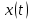 , , 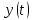 , , 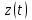 , … на отрезке , … на отрезке 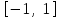 . Скалярное произведение определено равенством . Скалярное произведение определено равенством 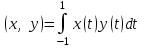 . Найти угол между векторами . Найти угол между векторами 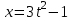 , , 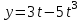 . .Решение. Имеем 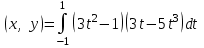 . Нетрудно заметить, что . Нетрудно заметить, что 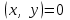 , так как подынтегральная функция является нечетной. Следовательно, векторы , так как подынтегральная функция является нечетной. Следовательно, векторы 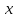 и и 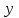 ортогональны. ортогональны.Задача 6 Задано евклидово пространство при 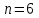 . Проверить справедливость теоремы Пифагора для ортогональных векторов . Проверить справедливость теоремы Пифагора для ортогональных векторов 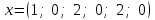 и и 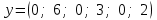 . . Решение. Имеем 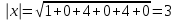 , , 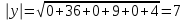 ; ;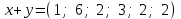 ; ; 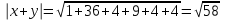 . .Итак, 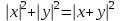 . .Задача 7 В евклидовом пространстве непрерывных функций рассматриваются два вектора: 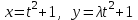 . Найти значение . Найти значение 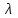 , при котором векторы , при котором векторы 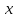 и и 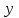 ортогональны на отрезке [0, 1], и проверить справедливость теоремы Пифагора для этих векторов. ортогональны на отрезке [0, 1], и проверить справедливость теоремы Пифагора для этих векторов.Решение. Составим скалярное произведение 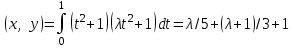 . .Из условия 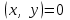 определяем определяем 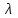 ; имеем ; имеем 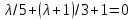 , откуда , откуда 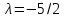 . .Найдем теперь длины векторов 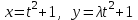 и и 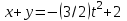 : :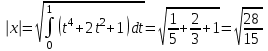 , ,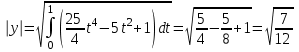 , ,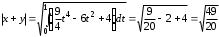 . .Таким образом, 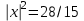 , , 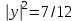 , , 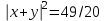 , т.е. , т.е. 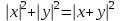 . .Задача 8 Приведем примеры линейных пространств: - множество 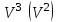 всех свободных векторов в пространстве (на плоскости) с линейными операциями над векторами – линейное пространство, так как верны все аксиомы линейного пространства; всех свободных векторов в пространстве (на плоскости) с линейными операциями над векторами – линейное пространство, так как верны все аксиомы линейного пространства;- множество всех геометрических векторов в пространстве с началом в данной точке и параллельных данной плоскости с линейными операциями над векторами является линейным пространством; - множество 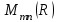 матриц типа матриц типа 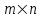 , элементами которых являются действительные числа, с линейными операциями над матрицами также удовлетворяет всем аксиомам линейного пространства; , элементами которых являются действительные числа, с линейными операциями над матрицами также удовлетворяет всем аксиомам линейного пространства;- множество матриц-строк (матриц-столбцов) длины 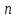 является линейным пространством относительно матричных операций сложения и умножения на число (это частный случай предыдущего примера); является линейным пространством относительно матричных операций сложения и умножения на число (это частный случай предыдущего примера);- множество 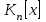 многочленов переменного многочленов переменного 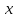 степени, не превышающей степени, не превышающей 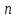 , которые как функции можно складывать и умножать на действительные числа; , которые как функции можно складывать и умножать на действительные числа;- множество всех решений данной однородной системы линейных алгебраических уравнений (СЛАУ). Решения можно рассматривать как матрицы-столбцы, складывать и умножать на числа по законам матричных операций. Столбец, получаемый в результате сложения решений или умножения решения на число, снова будет решением системы. Поэтому определены операции, подчиняющиеся аксиомам линейного пространства; - множество функций, непрерывных на отрезке, с обычными операциями сложения функций и умножения функции на число. При сложении непрерывных функций получаем непрерывную функцию, при умножении непрерывной функции на число также получаем непрерывную функцию. Поэтому сложение функций и умножение функций на число, не выводящие за пределы множества непрерывных на отрезке функций, можно рассматривать как операции линейного пространства. Легко убедиться, что для этих операций верны все аксиомы линейного пространства. Домашнее задание № 7 Задание 1 Будет ли система векторов линейно зависимой. а) 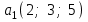 , , 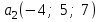 , , 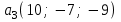 ; ;б) 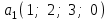 , , 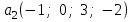 , , 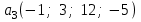 . .Ответ. а) да; б) да. Задание 2 Выяснить, образуют ли векторы 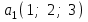 , , 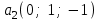 , , 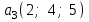 базис пространства базис пространства 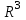 . .Задание 3 Убедиться, что векторы 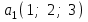 , , 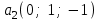 , , 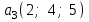 базис пространства базис пространства 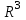 и найти координаты вектора и найти координаты вектора 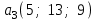 относительно нового базиса . относительно нового базиса .Задание 4 Найдите угол между векторами 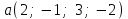 и и 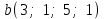 в евклидовом пространстве в евклидовом пространстве 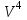 . .Ответ. 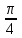 . .Задание 5 Является ли линейным подпространством соответствующего векторного пространства каждая из следующих совокупностей векторов: а) все векторы 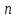 -мерного векторного пространства, координаты которых – целые числа? -мерного векторного пространства, координаты которых – целые числа?б) все векторы плоскости, каждый из которых лежит на одной из осей координат 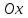 и и 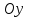 ? ?в) все векторы плоскости, начала и концы которых лежат на данной прямой? г) все векторы плоскости трехмерного пространства, концы которых не лежат на данной прямой. Ответ. а) не является; б) не является; в) является; г) не является. Задание 6 Является ли линейным пространством множество систем четырех действительных чисел 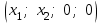 , , 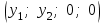 , , 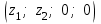 , где , где 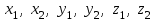 - всевозможные действительные числа? Сложение элементов и умножение на действительное число определены обычно. - всевозможные действительные числа? Сложение элементов и умножение на действительное число определены обычно.Ответ. Да. Задача 7 Образует ли линейное пространство множество элементов 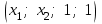 , , 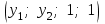 , , 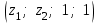 ? ?Ответ. Нет, т.к. сумма двух элементов множества не является элементом данного множества. Задача 8 Образует ли линейное пространство множество всевозможных многочленов второй степени 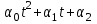 , , 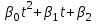 , , 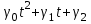 , …? , …?Ответ. Нет, так как сумма двух многочленов второй степени может быть многочленом первой степени или постоянной величиной. Задача 8 Образует ли линейное пространство множество всех многочленов не выше третьей степени? Ответ. Да. |
