64_90_Глава 4 Векторная алгебра. Векторная алгебра
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
§ 3 Векторное произведение двух векторов. Смешанное произведение трех векторов. Геометрический смысл векторов и смешанного произведения Три некомпланарных вектора  , ,  и и 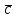 , взятые в указанном порядке, образуют правую (левую) тройку, если с конца вектора , взятые в указанном порядке, образуют правую (левую) тройку, если с конца вектора 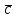 кратчайший поворот от первого вектора кратчайший поворот от первого вектора  ко второму вектору ко второму вектору  виден совершающимся против часовой стрелки, (соотв. По часовой стрелке) (рисунок 17). виден совершающимся против часовой стрелки, (соотв. По часовой стрелке) (рисунок 17). 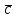  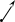 правая тройка правая тройка 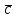 левая тройка левая тройка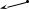 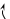     Рисунок 17 Векторным произведением неколлинеарных векторов  и и  называют вектор называют вектор 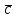 , определяемый условиями: , определяемый условиями:вектор 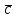 перпендикулярен векторам перпендикулярен векторам  и и  , т.е. , т.е. 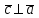 , , 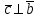 ; ;длина вектора 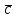 произведению длин векторов произведению длин векторов  и и  на синус угла между ними. на синус угла между ними.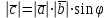 , , 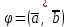 . (19) . (19)Векторы  , ,  и и 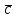 образуют правую тройку. образуют правую тройку.Векторное произведение обозначается 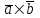 или или 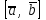 . .Если векторы  и и  коллинеарны (в частности, один из этих векторов нулевой), то по определению коллинеарны (в частности, один из этих векторов нулевой), то по определению 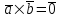 . .Свойства векторного произведения: 1. 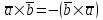 ; ;2. 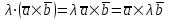 ; ;3. 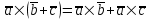 ; ;4. 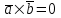 , если , если 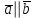 (или (или 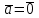 , или , или 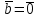 ). В частности ). В частности 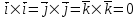 . .Формула векторного произведения двух векторов  и и  . .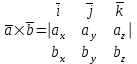 , или , или 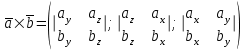 . (20) . (20)Геометрический смысл векторного произведения двух векторов:  Площадь параллелограмма, построенного на векторах Площадь параллелограмма, построенного на векторах  и и  , как на сторонах, равна длине векторного произведения: , как на сторонах, равна длине векторного произведения: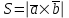 . .  (21) (21) Площадь треугольника: 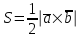 . (22) . (22)Смешанным произведениемтрех векторов  , ,  и и 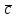 называется число равное скалярному произведению вектора называется число равное скалярному произведению вектора 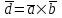 на вектор на вектор 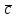 . (23) . (23)Обозначение: 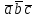 . .Таким образом: 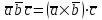 . .Смешанное произведение векторов  , ,  и и 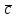 положительно, если данные векторы образуют правую тройку, и отрицательно – если левую. положительно, если данные векторы образуют правую тройку, и отрицательно – если левую.Свойства смешанного произведения: 1. 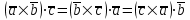 , т. е. смешанное произведение не меняется при циклической перестановке векторов; , т. е. смешанное произведение не меняется при циклической перестановке векторов;2. 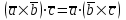 , т. е. смешанное произведение не меняется при перестановке знаков векторного и скалярного умножения; , т. е. смешанное произведение не меняется при перестановке знаков векторного и скалярного умножения;3. 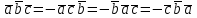 , т.е. смешанное произведение меняет знак на противоположный при перемене мест любых векторов-сомножителей; , т.е. смешанное произведение меняет знак на противоположный при перемене мест любых векторов-сомножителей;4. 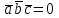 , если , если  , ,  и и 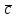 компланарны (в частности, если любые два из перемножаемых вектора коллинеарны). компланарны (в частности, если любые два из перемножаемых вектора коллинеарны).Если векторы  , ,  и и 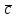 заданы своими координатами заданы своими координатами 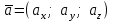 , , 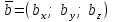 , , 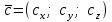 , то , то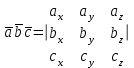 (24) (24)- формула смешанного произведениях трех векторов  , ,  и и 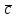 . .Если 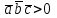 , то , то  , ,  , , 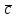 - правая тройка; - правая тройка; 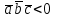 - левая. - левая.Геометрический смысл смешанного произведения трех векторов Объем параллелепипеда, построенного на векторах  , ,  и и 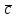 , как на ребрах, равен модулю смешанного произведения трех векторов , как на ребрах, равен модулю смешанного произведения трех векторов  , ,  и и 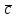 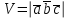 . (25) . (25)Объем треугольной пирамиды: 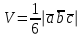 . (26) . (26)Три (и более) вектора называются компланарными, если они лежат в одной плоскости или в ||-ных плоскостях. Признак компланарности трех векторов Три вектора компланарны тогда и только тогда, когда их смешанное произведение равно нулю, т.е. 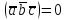 . .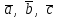 - компланарны - компланарны 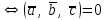 . (27) . (27)Практическое занятие № 9 Задание 1 Найти 1) 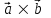 , 2) , 2) 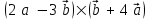 ; ; 3) 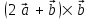 ; 4) ; 4) 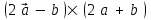 ). ).если 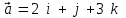 и и 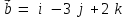 . .Решение. 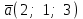 , , 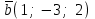 . .1) 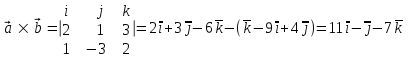 . .2) 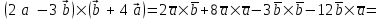 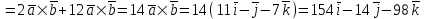 . .3) и 4) решите самостоятельно. Ответ. 1) 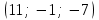 ; 3) ; 3) 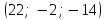 ; ; 2) 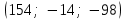 ; 4) ; 4) 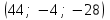 . .Задание 2 Найти площадь параллелограмма, с вершинами в точках  , , 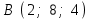 , , 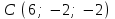 , , 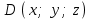 . .Решение. Используя геометрический смысл векторного произведения двух векторов найдем площадь параллелограмма 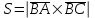 . .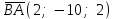 , , 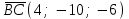 . .AB  DC Сначала вычислим векторное произведение двух векторов 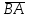 и и 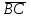 : :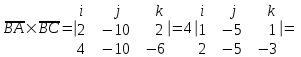 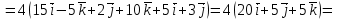 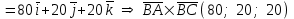 . .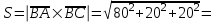 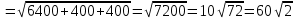 ед2. ед2.Ответ. 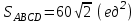 . .Задание 3 Определить площадь треугольника, построенного на векторах 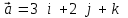 и и 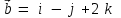 . .Решение. Вычислим площадь треугольника, используя геометрический смысл векторного произведения двух векторов  и и  : : 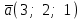 , , 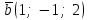 . .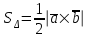 . .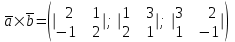 , , 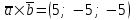 . .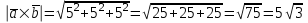 ед2. ед2.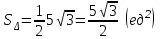 . .Ответ. 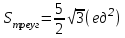 Задание 4 Вычислить площадь параллелограмма, построенного на векторах 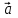 и и 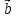 . . 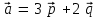 , , 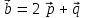 , , 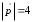 , , 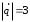 , , 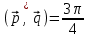 . .Решение. 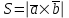 . .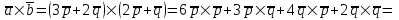 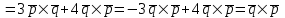 . .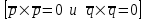 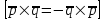 . .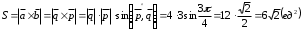 . .Ответ. 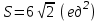 . .Задание 5 Найти 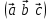 , если , если 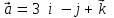 , , 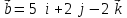 , , 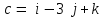 . .Решение. Используя формулу (24) вычислим смешанное произведение трех векторов 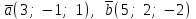 , , 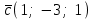 . .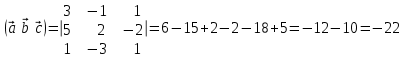 . .Ответ. 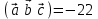 . .Задание 6 Выяснить какова ориентация тройки векторов 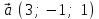 , , 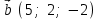 , , 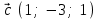 . .Ответ. левая. Задание 7 Найти объем параллелепипеда, построенного на векторах  , , 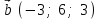 , , 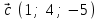 . .Решение. Используя геометрический смысл смешанного произведения трех векторов  , , 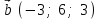 , , 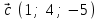 , вычислим объем: , вычислим объем: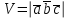 . .Сначала найдем смешанное произведение трех векторов 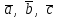 : :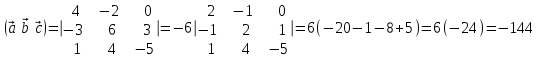 . .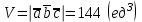 . .Ответ. 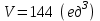 . .Задание 8 Доказать, что 4 точки 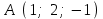 , , 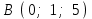 , , 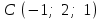 , , 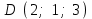 лежат в одной плоскости. лежат в одной плоскости.Решение. 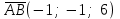 , , 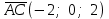 , , 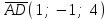 . .Точки 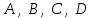 лежат в одной плоскости, если три вектора лежат в одной плоскости, если три вектора 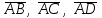 - компланарны, а по признаку компланарности трех векторов смешанное произведение трех векторов должно быть равно 0, т.е. - компланарны, а по признаку компланарности трех векторов смешанное произведение трех векторов должно быть равно 0, т.е. 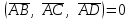 . .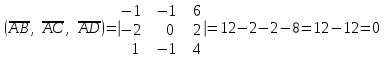 . .Ответ. Точки 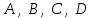 лежат в одной плоскости. лежат в одной плоскости. |
