64_90_Глава 4 Векторная алгебра. Векторная алгебра
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
Задание 9 Вычислить объем тетраэдра, вершины которого находятся в точках  , , 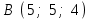 , , 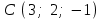 , , 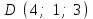 и высоту, опущенной из вершины и высоту, опущенной из вершины 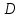 на грань на грань  . .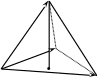 D DH B AC Решение. Используя геометрический смысл смешанного произведения трех векторов, вычислим объем тетраэдра: 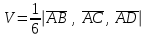 . .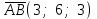 , , 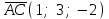 , , 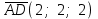 . .Найдем смешанное произведение трех векторов 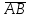 , , 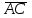 , , 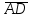 . .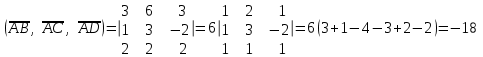 . .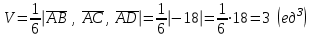 . .Из школьного курса известно, что объем тетраэдра равен: 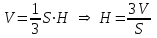 . .Найдем площадь основания. В основании лежит 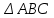 . Используя геометрический смысл векторного произведения двух векторов, найдем площадь грани . Используя геометрический смысл векторного произведения двух векторов, найдем площадь грани 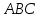 . .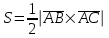 . .Найдем векторное произведение двух векторов 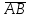 и и 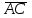 : :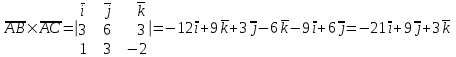 . .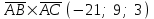 . .Найдем длину векторного произведения: 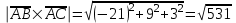 , т.к. , т.к. 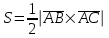 , то , то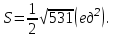 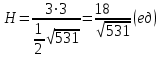 . .Ответ. 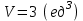 , , 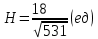 . .Домашнее задание № 9 Задание 1 Найти 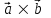 двух векторов, если двух векторов, если 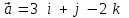 и и 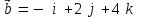 . .Ответ. 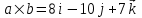 . .Задание 2 1) Найти площадь параллелограмма, построенного на векторах 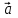 и и 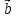 . . 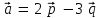 , , 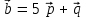 , , 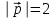 , , 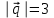 , , 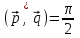 . .Ответ. 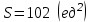 . .2) Найти площадь треугольника с вершинами в точках 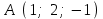 , , 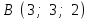 , ,  . .Ответ. 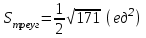 . .3) Даны вершины тетраэдра 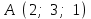 , , 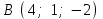 , , 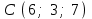 , , 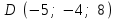 . Найти длину высоты, опущенной из вершины D . ( . Найти длину высоты, опущенной из вершины D . (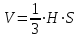 ). ).Ответ. 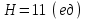 . .Задание 3 1) Установить компланарны ли вектора 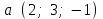 , , 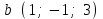 , , 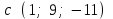 . .Ответ. да. Задание 4 Даны вектора 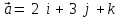 , , 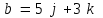 , , 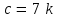 . Найти . Найти 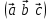 . .Ответ. 70. Вопросы для самопроверки Что называется линейной комбинацией? Какие векторы называются линейно зависимыми? Какие векторы называются линейно независимыми? Что называется скалярным произведением двух векторов? (Дайте определение через угол и через координаты) в 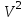 или или 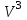 ? ?Сформулируйте признак перпендикулярности двух векторов. Дайте определение коллинеарности двух векторов. Сформулируйте признак коллинеарности двух векторов. Дайте определение векторного произведения двух векторов. Сформулируйте геометрический смысл векторного произведения двух векторов? Дайте определение смешанного произведения трех векторов. Сформулируйте геометрический смысл смешанного произведения трех векторов Дайте определение компланарности трех векторов. Сформулируйте признак компланарности трех векторов. Точки 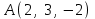 и и 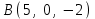 . Найти координаты . Найти координаты 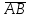 и и 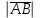 . .Даны два вектора 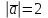 , , 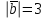 и угол между этими векторами равен и угол между этими векторами равен 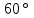  . Постройте два вектора . Постройте два вектора 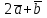 и и 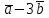 . .Найдите скалярное произведение двух векторов  и и  , если , если 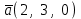 и и 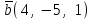 . .Найти векторное произведения двух векторов 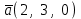 и и 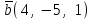 . .Проверить коллинеарность векторов 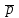 и и 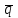 , если , если 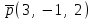 , , 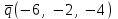 . .Найти смешанное произведение трех векторов  , ,  и и 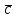 , если , если 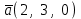 , , 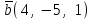 и и 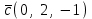 . .Сформулируйте определение базиса. Какие вектора называются равными? Что такое ортвектор. Дайте определение евклидова пространства. Сформулируйте определение нормы вектора евклидова пространства. Сформулируйте теорему Пифагора в 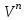 . .Как определяется угол между векторами евклидового пространства? Сформулируйте определение ортонормированного базиса. Сформулируйте определение линейного пространства. Какие векторы называются ортогональными? Сформулируйте теорему Коши-Буняковского. |
