64_90_Глава 4 Векторная алгебра. Векторная алгебра
 Скачать 0.89 Mb. Скачать 0.89 Mb.
|
|
§ 2 Векторы. Операции над векторами в V2 и V3. Скалярное произведение векторов Вектором в 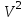 и и 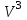 называется направленный отрезок. Вектор с началом в точке называется направленный отрезок. Вектор с началом в точке 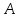 и концом в точке и концом в точке 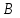 обозначается символом обозначается символом 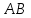 (или одной буквой, (или одной буквой,  , ,  , …). Длина отрезка , …). Длина отрезка 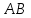 называется длиной, или модулем вектора называется длиной, или модулем вектора 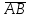 и обозначается и обозначается 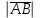 , , 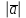 . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается . Вектор, длина которого равна нулю, называется нулевым вектором и обозначается 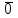 или просто 0. или просто 0.Вектор, длина которого равна единице, называется единичным вектором и обозначается через 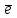 . .Единичный вектор, направление которого совпадает с направлением вектора  , называется ортомвектора а и обозначается , называется ортомвектора а и обозначается 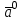 . Два ненулевых вектора называются противоположными, если они имеют одинаковую длину и противоположные направления. Вектор, противоположный вектору а, обозначается . Два ненулевых вектора называются противоположными, если они имеют одинаковую длину и противоположные направления. Вектор, противоположный вектору а, обозначается 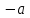 ; вектор ; вектор 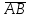 противоположен вектору противоположен вектору 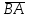 ( (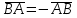 ). ).Векторы  и и  называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают называются коллинеарными, если они лежат на одной прямой или на параллельных прямых; записывают 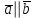 . . Два коллинеарных вектора  и и  называются равными( называются равными( = =  ), если они сонаправлены и имеют равные длины. ), если они сонаправлены и имеют равные длины.Совместим параллельным переносом начала неколлинеарных векторов  и и  . Начало и концы векторов образуют вершины треугольника. Углом между векторами . Начало и концы векторов образуют вершины треугольника. Углом между векторами  и и  называется угол при вершине этого треугольника, соответствующий началу векторов. Если векторы сонаправлены, то угол между ними равен нулю; если противоположно направлены – угол между ними равен 180°. называется угол при вершине этого треугольника, соответствующий началу векторов. Если векторы сонаправлены, то угол между ними равен нулю; если противоположно направлены – угол между ними равен 180°.Суммойдвух векторов  и и  называется вектор называется вектор 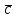 , соединяющий начало вектора , соединяющий начало вектора  с концом вектора с концом вектора  , отложенного от конца вектора , отложенного от конца вектора  . .Обозначение: 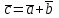 . .Для геометрического представления суммы векторов используют правила «треугольника» и «параллелограмма», проиллюстрированные на рисунках 14 и 15 соответственно. Под разностью векторов  и и  понимается вектор понимается вектор 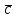 такой, что такой, что 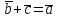 . Обозначение: . Обозначение: 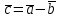 . Справедливо равенство . Справедливо равенство 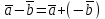 . .     А А  О 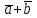 В ВРисунок 14         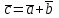   О  Рисунок 15 Произведением вектора 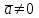 на число на число 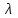 называется вектор, который имеет длину называется вектор, который имеет длину 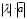 , его направление совпадает с вектором , его направление совпадает с вектором  , если , если 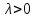 и противоположное направление, если и противоположное направление, если 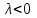 . .Обозначение: 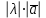 . .Отметим, что 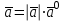 , т.е. каждый вектор равен произведению его модуля на орт. , т.е. каждый вектор равен произведению его модуля на орт.Два ненулевых вектора  и и  коллинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число, т.е. коллинеарны тогда и только тогда, когда один из них есть произведение другого на некоторое число, т.е. 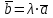 , , 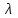 - число (признак коллинеарности векторов). - число (признак коллинеарности векторов).Три ненулевых вектора  , ,  , , 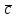 компланарны тогда и только тогда, когда один из них является линейной комбинацией других, например, компланарны тогда и только тогда, когда один из них является линейной комбинацией других, например, 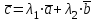 ( (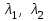 - числа не равные нулю одновременно) (признак компланарности векторов). - числа не равные нулю одновременно) (признак компланарности векторов).Если 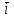 , , 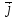 , , 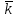 - орты координатных осей прямоугольной системы координат Oxyz,то любой вектор - орты координатных осей прямоугольной системы координат Oxyz,то любой вектор  единственным образом можно представить в виде их суммы (линейной комбинации) с коэффициентами ах, ауи az: единственным образом можно представить в виде их суммы (линейной комбинации) с коэффициентами ах, ауи az: 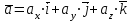 .Коэффициенты ах, ауи azлинейной комбинации называют координатами вектора .Коэффициенты ах, ауи azлинейной комбинации называют координатами вектора  в базисе в базисе 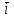 , , 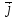 , , 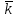 . Координаты ах, ау, azвектора . Координаты ах, ау, azвектора  - это его проекции на соответствующие координатные оси. Вектор - это его проекции на соответствующие координатные оси. Вектор  с координатами ах, ау, azзаписывают в виде с координатами ах, ау, azзаписывают в виде 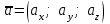 . Длина вектора . Длина вектора  определяется по формуле определяется по формуле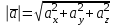 , ,где 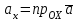 (проекция вектора (проекция вектора  на ось ОХ), на ось ОХ),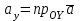 (проекция вектора (проекция вектора  на ось ОY), на ось ОY),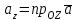 (проекция вектора (проекция вектора  на ось ОZ). на ось ОZ).Вектор  образует с координатными осями Ох, Оу и Ozуглы образует с координатными осями Ох, Оу и Ozуглы 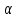 , , 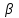 и и 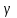 соответственно. Направление вектора соответственно. Направление вектора  определяется с помощью направляющих косинусов: определяется с помощью направляющих косинусов: 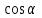 , , 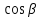 , , 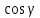 для которых справедливы равенства для которых справедливы равенства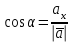 , , 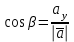 , , 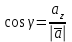 . (13) . (13)Направляющие косинусы связаны соотношением 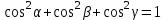 . (14) . (14)Пусть даны два вектора 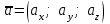 и и 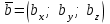 . Тогда: . Тогда: 1) векторы  и и  равны тогда и только тогда, когда равны их соответствующие координаты, т.е. равны тогда и только тогда, когда равны их соответствующие координаты, т.е. 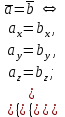 (15) (15)2) векторы  и и  коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е. коллинеарны тогда и только тогда, когда их соответствующие координаты пропорциональны, т.е.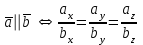 . (16) . (16)При сложении векторов их одноименные координаты складывающем, вычитании – вычитаются, при умножении вектора на число – умножаются на это число: 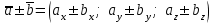 , ,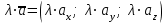 Вектор 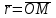 , соединяющий начало координат с произвольной точкой , соединяющий начало координат с произвольной точкой 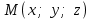 пространства называется радиус-векторомточки М. Координаты точки – это координаты ее радиус-вектора пространства называется радиус-векторомточки М. Координаты точки – это координаты ее радиус-вектора 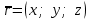 или или 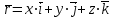 . Если вектор . Если вектор 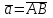 задан точками задан точками 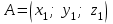 и и 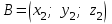 то его координаты ах, ау, azвычисляются по формулам то его координаты ах, ау, azвычисляются по формулам 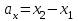 , , 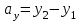 , , 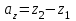 : :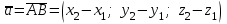 . .1 Скалярным произведением двух ненулевых векторов  и и  называется число, равное произведению длин этих векторов на косинус угла называется число, равное произведению длин этих векторов на косинус угла 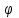 между ними (рисунок 16). между ними (рисунок 16).Обозначение: 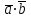 . .Таким образом, 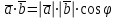 . (17) . (17)      ) φ   Рисунок 16 Свойства скалярного произведения: 1. 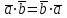 . .2. 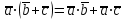 3. 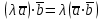 . .4. 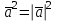 . .5. 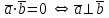 (или (или 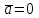 , или , или 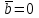 ). В частности: ). В частности: 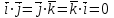 . .Векторы  и и  заданы своими координатами заданы своими координатами 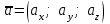 и и 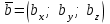 . .2 Скалярным произведением двух ненулевых векторов  и и  называется число, равное сумме произведений их координат называется число, равное сумме произведений их координат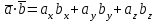 . (18) . (18)Практическое занятие № 8 Задача 1 Даны два вектора  и и  . Построить векторы: . Построить векторы: 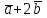 , , 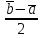 ; ; 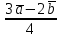 . .Задача 2 Вычислите направляющие косинусы 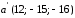 . .Решение. 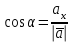 , , 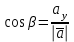 , , 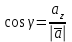 . .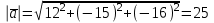 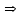 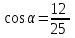 , , 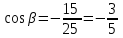 , , 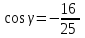 . .Ответ: 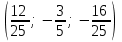 . .Задача 3 Может ли 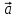 с координатными осями составлять следующие углы: с координатными осями составлять следующие углы:1) 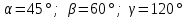 ; 2) ; 2) 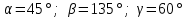 ; ;3) 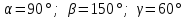 . .Решение. 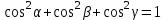 . .1) 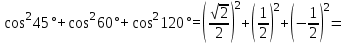 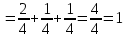 . .Ответ: а) да; б) нет; в) да. Задача 4 Проверить коллинеарность векторов 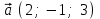 и и 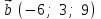 . .Решение. 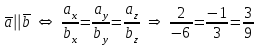 . . 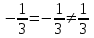 . .Ответ. нет. Задача 5 При каких значениях 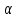 и и 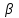 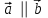 : : 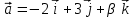 и и 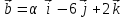 ? ?Решение. 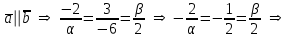 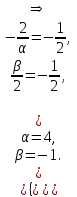 Ответ: 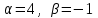 . .Задача 6 Известно: 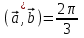 , , 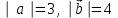 . Вычислить: . Вычислить:а) 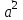 ; б) ; б) 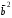 ; в) ; в) 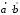 ; ; г) 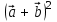 ; д) ; д) 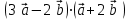 ; е) ; е) 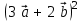 . .Решение. а) 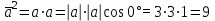 ; ;б) 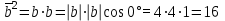 ; ;в) 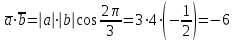 ; ;г) 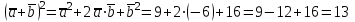 ; ;д) 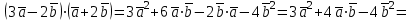 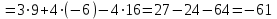 . .Ответ: а) 9; б) 16; в) – 6; г) 13; д) – 61; е) 73. Задача 7. Проверить при каком значении 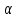 векторы векторы 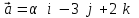 и и 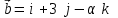 взаимноперпендикулярны? взаимноперпендикулярны?Решение. 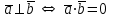 . .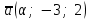 , , 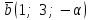 . .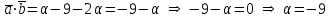 . .Ответ: 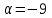 . .Задача8 Вычислить косинус угла, образованного векторами 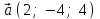 и и 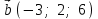 . .Решение. По формуле (17), выразим косинус угла между двумя векторами  и и  : :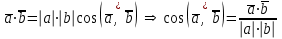 . .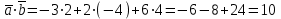 , ,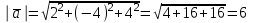 , ,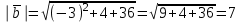 , ,т.о. 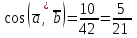 . .Ответ: 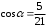 . .Задача 9 Даны вершины треугольника 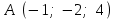 , , 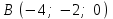 , , 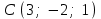 . Определите внутренний угол при вершине В. . Определите внутренний угол при вершине В.Решение. 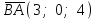 , , 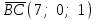 . .  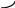 В   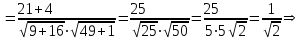 А С 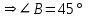 . .Ответ: 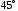 . .Задача 10 Вектор 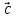 , коллинеарный вектору , коллинеарный вектору 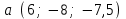 образует острый угол с осью OZ. Зная, что образует острый угол с осью OZ. Зная, что 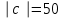 , найти его координаты. , найти его координаты.Решение. 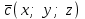 , , 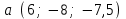 . .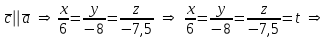 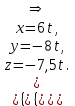 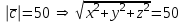 , ,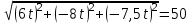 , ,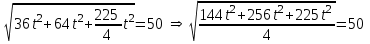 , ,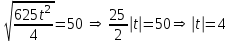 . .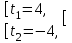 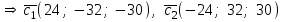 , ,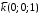 . .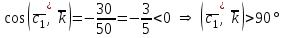 , ,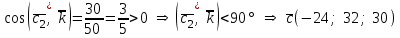 . .Ответ: 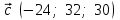 . .Задание 11 Найти 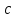 , зная, что он перпендикулярен к векторам , зная, что он перпендикулярен к векторам 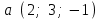 и и 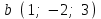 и удовлетворяет условию и удовлетворяет условию 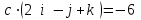 . .Решение. 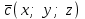 , , 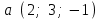 , , 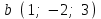 . .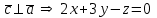 , , 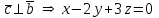 , , 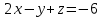 . .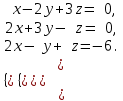 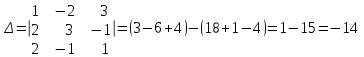 . .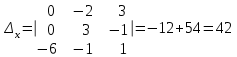 , , 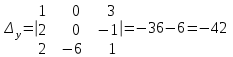 , ,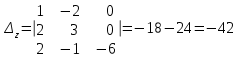 . .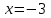 , , 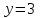 , , 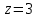 . .Ответ: 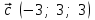 . .Задание 12 Даны три вектора 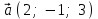 , , 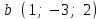 и и 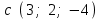 . Найти . Найти 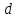 , удовлетворяющий условиям , удовлетворяющий условиям 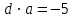 ; ; 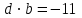 ; ; 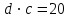 . .Решение. 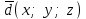 . .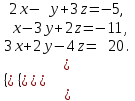 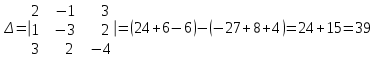 . .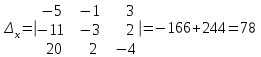 , ,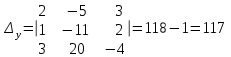 , , 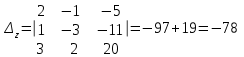 . .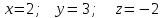 . .Ответ. 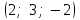 . .Домашнее задание № 8 Задание 1 Найдите орт-вектор для векторов: 1) 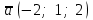 ; 2) ; 2) 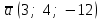 . .Ответ. 1) 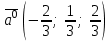 ; 2) ; 2) 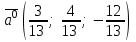 . .Задание 2 Вычислите направляющие косинусы 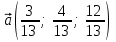 . .Ответ. 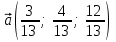 . .Задание 3 1) Может ли 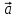 составлять с двумя координатными осями следующие углы: а) составлять с двумя координатными осями следующие углы: а) 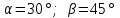 ; б) ; б) 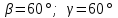 ; в) ; в) 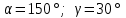 . .Ответ: а) нет; б) да; в) нет. 2) Вектор составляет с осями Ох и Оу следующие углы 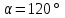 и и 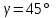 . Какой угол он составляет с осью Оу? . Какой угол он составляет с осью Оу?Ответ: либо 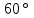 , либо , либо 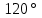 . .Задание 4 1) Даны точки 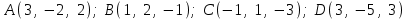 . Будут ли точки А, B, C, D образовывать трапецию? . Будут ли точки А, B, C, D образовывать трапецию?Ответ: нет. 2) Проверить 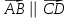 , если , если 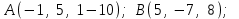 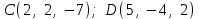 . .Задание 5 Известно, что 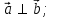 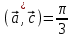 ; ; 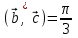 ; ; 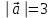 , , 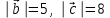 . . Вычислить: а) 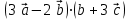 ; б) ; б) 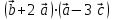 ; ;в) 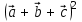 ; г) ; г) 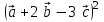 . .Ответ: а) – 62; б) – 114; в) 162; г) 373. Задание 6 Даны вершины треугольника 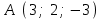 , , 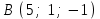 и и 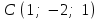 . Определите внутренние угла треугольника АВС. . Определите внутренние угла треугольника АВС.Ответ. 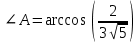 ; ; 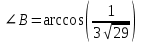 ; ; 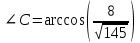 . .Задание 7 Найти координаты 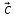 , если , если 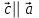 , , 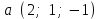 и и 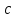 удовлетворяет условию удовлетворяет условию 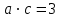 . .Ответ: 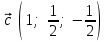 . .Задание 8 Вектор 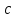 , перпендикулярный к векторам , перпендикулярный к векторам 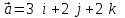 и и 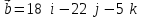 , и образует с осью OY тупой угол. Найти координаты , и образует с осью OY тупой угол. Найти координаты 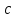 , зная, что , зная, что 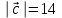 . .Ответ. 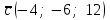 . . |
