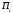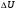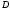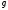Расчёт координат места судна-1. Вероятнейших координат местоположения судна по избыточным навигационным измерениям
 Скачать 3.07 Mb. Скачать 3.07 Mb.
|
|
2.1.3 Расчёт весовой матрицы 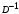 : : Весовой элемент: 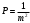 = =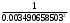 = =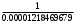 =82070.15875 =82070.15875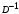 = = 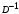 = = 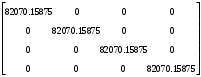 2.1.4 Расчёт промежуточной матрицы 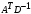 : :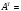 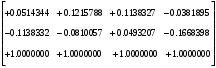 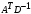 = = 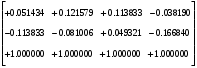 × ×× 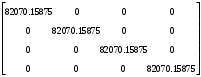 = == 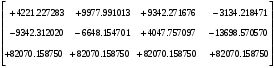 2.1.5 Расчёт матрицы коэффициентов нормального уравнения 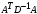 : : 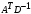 = =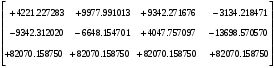 × ×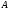 = == 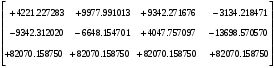 × ×× 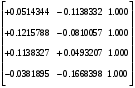 = == 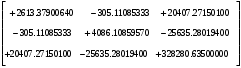 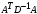 = =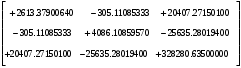 Det( 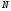 )=375120515120 )=3751205151202.1.6 Расчёт ковариационной матрицы погрешностей географических координат: 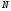 = =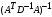 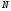 = = 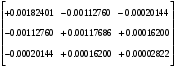 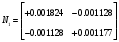 2.1.7 Расчёт псевдообратной матрицы 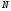 × × 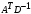 : :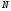 × ×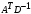 = =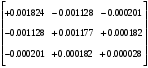 × ×× 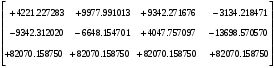 = == 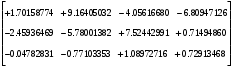 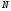 × × 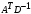 = =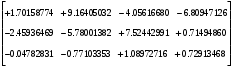 2.1.8 Расчёт вектора искомых неизвестных 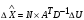 : :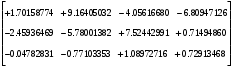 × × = =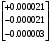 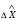 = =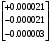 → вектор решений → вектор решений∆ 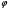 → ∆ 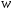 ∆ 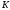 =0.050294–0.000003=0.0502291 =0.050294–0.000003=0.0502291∆ 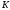 = 0.050291×180/ = 0.050291×180/ =2.881462048°=2.881459≈2.8815°≈2.882° =2.881462048°=2.881459≈2.8815°≈2.882°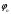 = =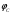 +∆ +∆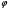 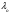 = =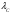 +∆ +∆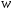 / cos60°= / cos60°=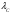 +∆ +∆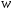 /0.5= /0.5=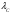 +2×∆ +2×∆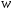 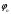 =59°58'24.28''N +0.000021=+59°58.404635'+0.000021'=+59°58.404656'= =59°58'24.28''N +0.000021=+59°58.404635'+0.000021'=+59°58.404656'==59°58'24.27936"N (0. 404656'×60"=24.27936") 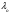 =69°44'23.56"W +2×(–0.000021)=–69°44.39267'–0.000042'=–69°44.392712'= =69°44'23.56"W +2×(–0.000021)=–69°44.39267'–0.000042'=–69°44.392712'==69°44.392712'W=69°44'23.56272"W (0.392712'×60''=23.56272")
2.1.9 Расчёт невязки (вектор из счислимой точки в обсервованную): 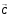 =arctg(∆ =arctg(∆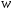 /∆ /∆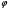 )=arctg(0.000021/–0.000021)=arctg(–1.0)=45° )=arctg(0.000021/–0.000021)=arctg(–1.0)=45°(направление вектора невязки) 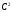 =∆ =∆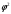 +∆ +∆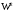 (теорема Пифагора) (теорема Пифагора)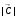 = =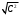 (величина невязки) (величина невязки)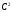 = =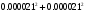 =0.000000000441+0.000000000441=0.000000000882 =0.000000000441+0.000000000441=0.000000000882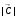 = =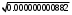 =0.00002969848481≈0.00003. =0.00002969848481≈0.00003.2.2 ОЦЕНКА ТОЧНОСТИ ОБСЕРВАЦИИ ПО ВТОРОЙ ИТЕРАЦИИ Из пункта 6 используем определённую ковариационную матрицу 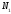 : :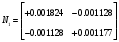 В общем виде ковариационную матрицу 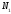 можно определить следующим образом: можно определить следующим образом: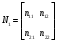 , ,где: 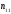 – дисперсия погрешностей – дисперсия погрешностей 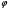 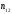 – дисперсия погрешностей – дисперсия погрешностей 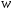 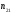 = =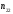 – ковариационные моменты – ковариационные моменты2.2.1 Расчёт априорной точности обсервации: 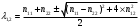 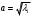 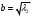 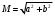 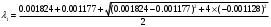 = == 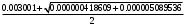 = == 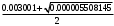 = =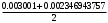 = =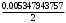 =0.002673971879 =0.002673971879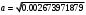 =0.051710461×1852 м = 95.7677756 м ≈ 95.8 м =0.051710461×1852 м = 95.7677756 м ≈ 95.8 м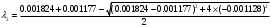 = == 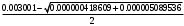 = =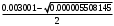 = == 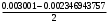 = =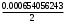 =0.0003270281215 =0.0003270281215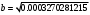 =0.18083918 ×1852 м = 33.49141774 м ≈ 33.5 м =0.18083918 ×1852 м = 33.49141774 м ≈ 33.5 мУгол наклона большей полуоси  относительно норда: относительно норда:Ψ = arctg ( 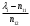 ) )Ψ = arctg( 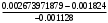 ) = arctg( ) = arctg(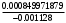 ) = arctg(–0.753521169)= ) = arctg(–0.753521169)==– 36.99879838° + 180° = 143.0012016° ≈ 143.0° 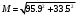 = = 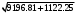 = = 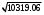 =101.5827741 ≈ 101.6 м =101.5827741 ≈ 101.6 м2.2.2 Расчёт апостериорной точности обсервации – аналогично первой итерации! 3.1 ГРАФОАНАЛИТИЧЕСКИЙ РАСЧЁТ (ПЕРВАЯ ИТЕРАЦИЯ)
|