Расчёт координат места судна-1. Вероятнейших координат местоположения судна по избыточным навигационным измерениям
 Скачать 3.07 Mb. Скачать 3.07 Mb.
|
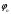 =59°58.4'+0.004635'=59°58.404635'N=59°58'24.28''N =59°58.4'+0.004635'=59°58.404635'N=59°58'24.28''N (0.404636'×60''=24.2781") 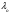 =69°44.4'W+2×0.003665'E=–69°44.4'+0.00733'=69°44.39267'W=69°44'23.56"W =69°44.4'W+2×0.003665'E=–69°44.4'+0.00733'=69°44.39267'W=69°44'23.56"W (0.39267'×60''=23.5602")
1.1.9 Расчёт невязки (вектор из счислимой точки в обсервованную): 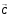 =arctg(∆ =arctg(∆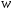 /∆ /∆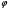 )=arctg(0.003665/0.004635)=arctg(0.790722761)=38.33422454°≈38.3° )=arctg(0.003665/0.004635)=arctg(0.790722761)=38.33422454°≈38.3°(направление вектора невязки в градусах) 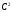 =∆ =∆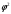 +∆ +∆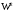 ( теорема Пифагора с катетами ∆ ( теорема Пифагора с катетами ∆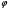 и ∆ и ∆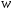 ). ).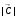 = =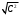 ( величина невязки ). ( величина невязки ).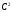 = =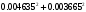 =0.000021483225+0.000013432225=0.00003491545 =0.000021483225+0.000013432225=0.00003491545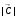 = =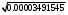 =0.005908929683≈0.005909. =0.005908929683≈0.005909. 1.2 ОЦЕНКА ТОЧНОСТИ ОБСЕРВАЦИИ Из пункта 6 используем определённую ковариационную матрицу 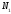 : :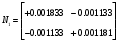 В общем виде ковариационную матрицу 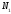 можно определить следующим образом: можно определить следующим образом: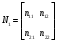 , ,где: 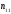 – дисперсия погрешностей – дисперсия погрешностей 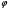 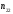 – дисперсия погрешностей – дисперсия погрешностей 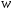 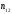 = =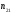 – ковариационные моменты – ковариационные моменты1.2.1 Расчёт априорной точности обсервации: Вычисление собственных чисел как экстремальных значений дисперсий: 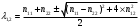 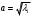 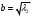 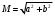 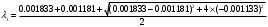 = == 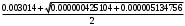 = == 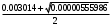 = =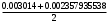 = =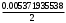 =0.002685967769 =0.002685967769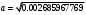 =0.051826323×1852 м = 95.98235043 м ≈ 96.0 м =0.051826323×1852 м = 95.98235043 м ≈ 96.0 м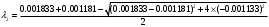 = == 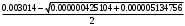 = =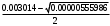 = == 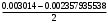 = =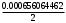 =0.000328032231 =0.000328032231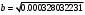 =0.1811166 ×1852 м = 33.54279448 м ≈ 33.5 м =0.1811166 ×1852 м = 33.54279448 м ≈ 33.5 мУгол наклона большей полуоси  относительно норда: относительно норда:Ψ = arctg ( 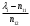 ) )Ψ = arctg( 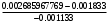 ) = arctg( ) = arctg(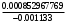 ) = arctg(–0.752840043)= ) = arctg(–0.752840043)==– 36.97389815° + 180° = 143.0261018° ≈ 143.0° 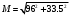 = = 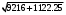 = = 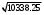 =101.6771852 ≈ 101.7 м =101.6771852 ≈ 101.7 м1.2.2 Расчёт апостериорной точности обсервации: Формирование вектора невязок 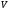 = =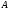 × ×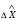 – – 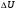 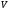 = = 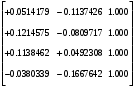 × ×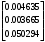 – – 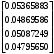 = =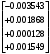 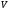 = = 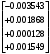 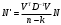 , ,где: 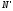 – апостериорная ковариационная матрица погрешностей координат – апостериорная ковариационная матрица погрешностей координат – количество уравнений ( – количество уравнений ( =4) =4)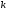 – количество неизвестных ( – количество неизвестных (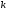 =3) =3)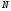 – априорная ковариационная матрица погрешностей географических координат – априорная ковариационная матрица погрешностей географических координат (пункт 6) 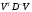 = = 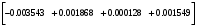 × ×× 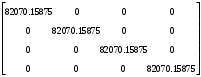 × × 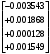 =1.514264 ≈ 1.5143 =1.514264 ≈ 1.5143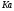 = 1.5143 = 1.5143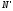 = 1.514264 × = 1.514264 × 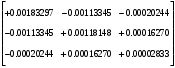 = == 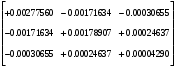 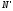 = = 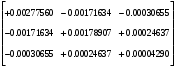 верхний левый блок 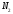 = = 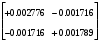 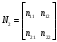 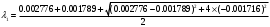 = == 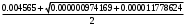 = == 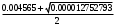 = =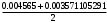 = =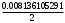 =0.004068052646 =0.004068052646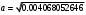 =0.063781287×1852 м = 118.1229446 м ≈ 118.1 м =0.063781287×1852 м = 118.1229446 м ≈ 118.1 м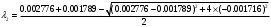 = == 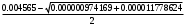 = =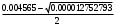 = == 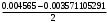 = =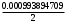 =0.0004969473545 =0.0004969473545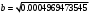 =0.022292316 ×1852 м = 41.28536931 м ≈ 41.3 м =0.022292316 ×1852 м = 41.28536931 м ≈ 41.3 мУгол наклона большей полуоси  относительно норда: относительно норда:Ψ = arctg ( 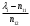 ) )Ψ = arctg( 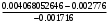 ) = arctg( ) = arctg(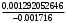 ) = arctg(–0.752944432)= ) = arctg(–0.752944432)==– 36.9777154° + 180° = 143.0222846° ≈ 143.0° 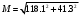 = = 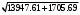 = = 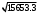 =125.1131488 ≈ 125.1 м =125.1131488 ≈ 125.1 м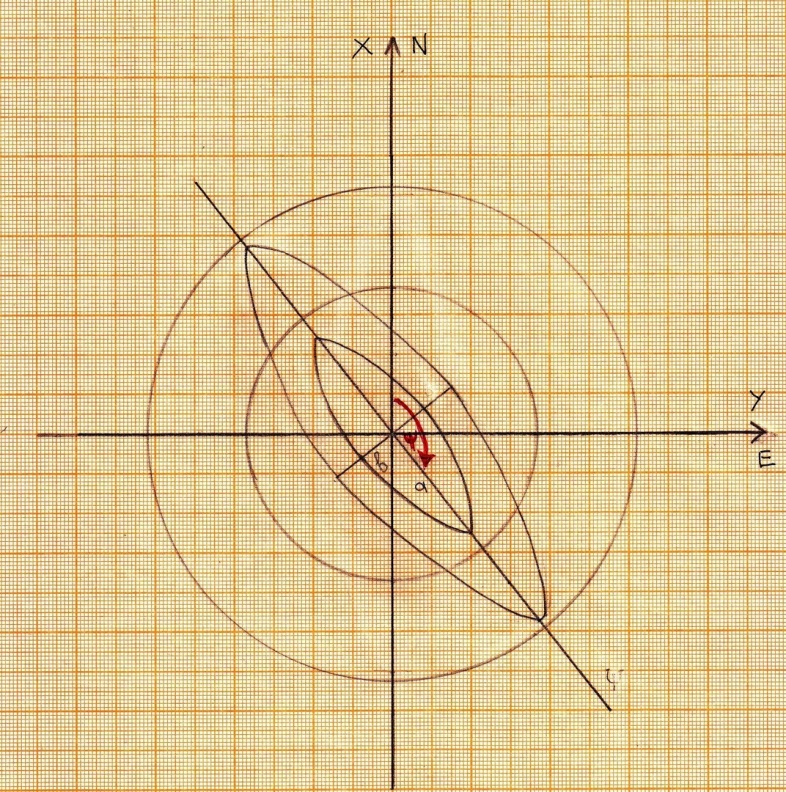 Рис. 1.2.1 Априорная и апостериорная оценка точности обсервации по первой итерации 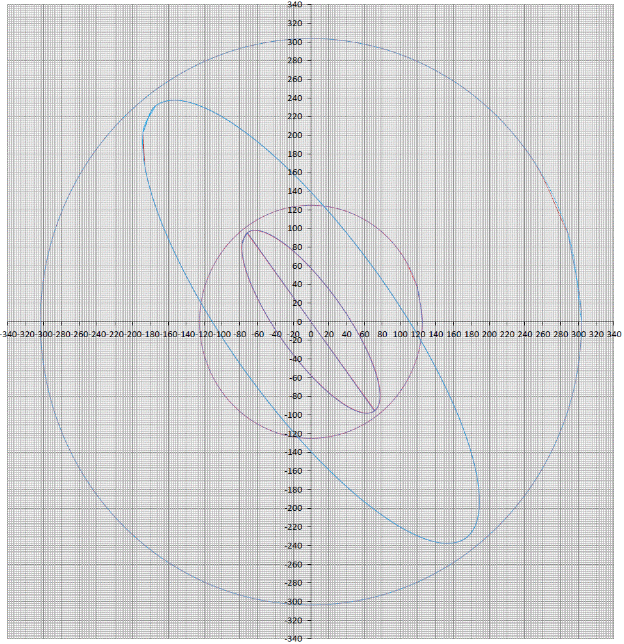 Рис. 1.2.2 Иллюстративный показательный пример априорной и апостериорной оценки точности обсервации (не соответствует условиям задачи для использования в качестве примера возможного оформления) 2.1 ВТОРАЯ ИТЕРАЦИЯ РАСЧЁТА КООРДИНАТ РЕЗУЛЬТАТЫ ПЕРВОЙ ИТЕРАЦИИ: 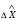 = =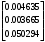 ∆ 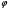 → ∆ 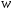 ∆ 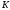 ∆ 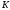 =+2.881624° =+2.881624°2.1.1 Формирование нового вектора 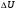 : :
Обсервованные координаты первой итерации принимаются за счислимые! π=3.141592653589793 Deg →Rad: ×  /180 /180Rad→ Deg: ×180/  СКП измерения пеленга m=0.2°=0.003490658503 радиан Промежуточная широта 60°N(S) 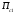 = arctg(∆ = arctg(∆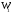 /∆ /∆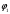 )=arctg(+3.296335/+7.295365)= =arctg(+0.451839626)=24.31533805°+2.881624°=27.19696205° )=arctg(+3.296335/+7.295365)= =arctg(+0.451839626)=24.31533805°+2.881624°=27.19696205°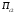 =arctg(∆ =arctg(∆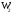 /∆ /∆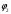 )=arctg(+5.6963335/+3.795365)= )=arctg(+5.6963335/+3.795365)==arctg(+1.500866188)=56.32519681°+2.881624°=59.20682081° 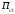 =arctg(∆ =arctg(∆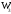 /∆ /∆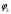 )=arctg(+7.396335/–3.204635)=arctg(–2.308011677)= )=arctg(+7.396335/–3.204635)=arctg(–2.308011677)=–66.57419969°+180°=113.4258003°+2.881624°=116.3074243° 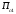 =arctg(∆ =arctg(∆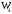 /∆ /∆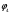 )=arctg(–1.303665/+5.695365)=arctg(–0.228899289)= )=arctg(–1.303665/+5.695365)=arctg(–0.228899289)=–12.89285262°+360°=347.1071474°+2.881624°=349.9887714° 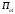 – –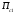 =27.4°–27.19696205°=0.20303795°×π/180=0.00354364 =27.4°–27.19696205°=0.20303795°×π/180=0.00354364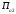 – –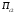 =59.1°–59.20682081°=–0.10682081°×π/180=–0.00186439 =59.1°–59.20682081°=–0.10682081°×π/180=–0.00186439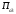 – –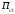 =116.3°–116.3074243°=–0.007424305°×π/180=–0.00012954 =116.3°–116.3074243°=–0.007424305°×π/180=–0.00012954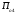 – –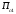 =349.9°–349.9887714°=–0.088771378°×π/180=–0.00154943 =349.9°–349.9887714°=–0.088771378°×π/180=–0.00154943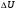 = = = =  Вектор – это частный случай матрицы! Вектор – это частный случай матрицы!2.1.2 Расчёт матрицы частных производных 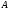 : :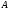 = = 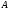 = = 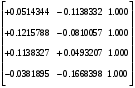 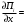 (∆ (∆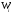 ) / (∆ ) / (∆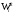 +∆ +∆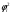 ) )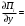 – (∆ – (∆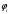 ) / (∆ ) / (∆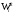 +∆ +∆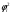 ) )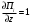 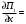 +3.296335/( +3.296335/(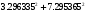 ) = 3.296335/(10.86582443+53.22235048) = ) = 3.296335/(10.86582443+53.22235048) == 3.296335/64.08817491 =0.051434371 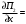 +5.696335/( +5.696335/(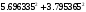 ) = 5.696335/(32.44823243+14.40479548) = =5.696335/46.85302791 =0.1215788001 ) = 5.696335/(32.44823243+14.40479548) = =5.696335/46.85302791 =0.1215788001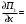 +7.396335/( +7.396335/(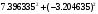 ) = 7.396335/(54.70577143+10.26968548) = =7.396335/64.97545691 =0.11383275 ) = 7.396335/(54.70577143+10.26968548) = =7.396335/64.97545691 =0.11383275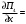 –1.303665/( –1.303665/(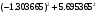 ) = –1.303665/(1.699542432+32.43718248) = ) = –1.303665/(1.699542432+32.43718248) == –1.303665/34.13672492 =–0.038189515 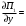 –7.295365/( –7.295365/(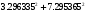 )=–7.295365/(10.86582443+53.22235048) = )=–7.295365/(10.86582443+53.22235048) ==–7.295365/64.08817491=–0.113833246 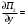 –3.795365/( –3.795365/(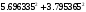 )=–3.795365/(32.44823243+14.40479548)= )=–3.795365/(32.44823243+14.40479548)==–3.795365/46.85302791=–0.081005757 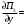 +3.204635/( +3.204635/(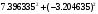 )= )==3.204635/(54.70577143+10.26968548)=3.204635/64.97545691=0.049320699 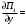 –5.695365/( –5.695365/(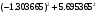 )=–5.695365/(1.699542432+32.43718248)= )=–5.695365/(1.699542432+32.43718248)= =–5.695365/34.13672492=–0.166839818 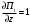 ; ; 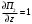 ; ;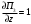 ; ; 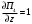 . . |