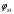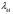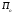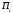Расчёт координат места судна-1. Вероятнейших координат местоположения судна по избыточным навигационным измерениям
 Скачать 3.07 Mb. Скачать 3.07 Mb.
|

И.В. Ююкин РАСЧЕТ ВЕРОЯТНЕЙШИХ КООРДИНАТ МЕСТОПОЛОЖЕНИЯ СУДНА ПО ИЗБЫТОЧНЫМ НАВИГАЦИОННЫМ ИЗМЕРЕНИЯМ Методические указания для курсовой работы по математическим основам судовождения Санкт-Петербург ГУМРФ имени адмирала. С.О. Макарова 2020 СТРАТЕГИЯ РАСЧЁТА КООРДИНАТ МНК 5 4  2 1 3 6 8 ТАКТИЧЕСКИХ ШАГОВ 7 АЛГОРИТМ 1. 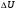 ─ вектор измерений навигационных параметров ─ вектор измерений навигационных параметров2. 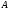 ─ матрица коэффициентов линий положения (матрица частных производных) ─ матрица коэффициентов линий положения (матрица частных производных)3. 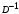 ─ весовая матрица ─ весовая матрица4. 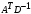 ─ промежуточная матрица ─ промежуточная матрица5. 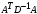 ─ матрица коэффициентов нормального уравнения ─ матрица коэффициентов нормального уравнения6. 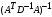 = =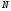 ─ ковариационная матрица погрешностей географических координат ─ ковариационная матрица погрешностей географических координат 7. 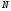 × ×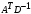 ─ псевдообратная матрица ─ псевдообратная матрица8. 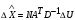 ─ вектор искомых неизвестных ─ вектор искомых неизвестных  — оптимальность решения по МНК — оптимальность решения по МНК1.1 ПЕРВАЯ ИТЕРАЦИЯ РСЧЕТА КООРДИНАТ 1.1.1 Расчёт вектора измерений навигационных параметров 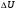 : :
π=3.141592653589793 Deg →Rad: ×  /180 /180Rad→ Deg: ×180/  СКП измерения пеленга m=0.2°=0.003490658503 радиан Промежуточная широта 60°N(S) 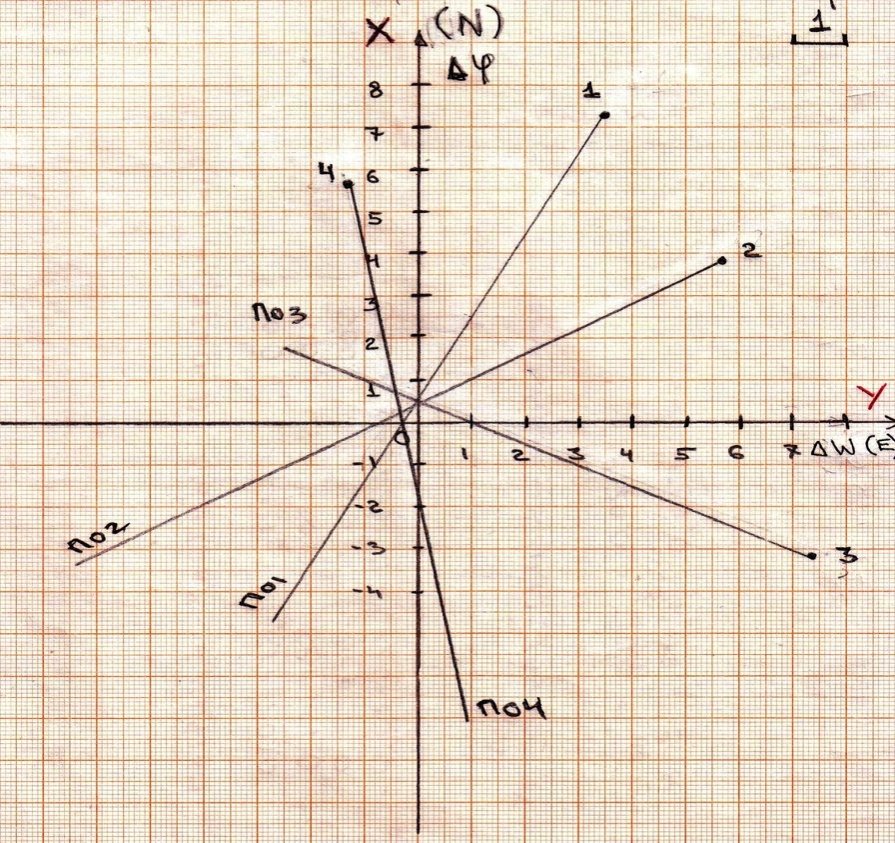 Рис. 1.1.1 Схема расположения навигационных ориентиров  Рис. 1.1.2 Иллюстративная показательная схема расположения навигационных ориентиров (не соответствует условиям задачи для использования в качестве примера возможного оформления) Вычисление arctg на калькуляторе CASIO fx-100MX: MODE: Deg Rad 1 2 SHIFT 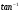 ANS = ANS = 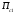 = arctg(∆ = arctg(∆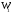 /∆ /∆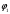 )=arctg(+3.3/+7.3)= arctg(+0.452054794)=24.32557523° )=arctg(+3.3/+7.3)= arctg(+0.452054794)=24.32557523°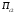 =arctg(∆ =arctg(∆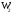 /∆ /∆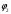 )=arctg(+5.7/+3.8)=arctg(+1.500000000)=56.30993247° )=arctg(+5.7/+3.8)=arctg(+1.500000000)=56.30993247°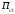 =arctg(∆ =arctg(∆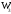 /∆ /∆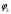 )=arctg(+7.4/–3.2)=arctg(–2.312500000)= –66.61477895°+180°= )=arctg(+7.4/–3.2)=arctg(–2.312500000)= –66.61477895°+180°==113.38522110° 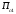 =arctg(∆ =arctg(∆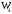 /∆ /∆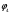 )=arctg(–1.3/+5.7)=arctg(–0.228070175)= –12.84770486°+360°= )=arctg(–1.3/+5.7)=arctg(–0.228070175)= –12.84770486°+360°==347.15229510° 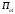 – –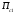 =27.4°–24.32557523°=3.07442477°×π/180=0.05365883 =27.4°–24.32557523°=3.07442477°×π/180=0.05365883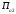 – –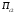 =59.1°–56.30993247°=2.790067526°×π/180=0.048695864 =59.1°–56.30993247°=2.790067526°×π/180=0.048695864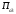 – –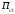 =116.3°–113.38522110°=2.91477890°×π/180=0.05087249 =116.3°–113.38522110°=2.91477890°×π/180=0.05087249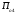 – –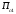 =349.9°–347. 15229510°=2.7477049°×π/180=0.04795650 =349.9°–347. 15229510°=2.7477049°×π/180=0.04795650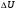 = = = =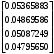 Вектор – это частный случай матрицы! Вектор – это частный случай матрицы!1.1.2 Расчёт матрицы частных производных 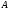 : :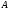 = = 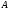 = = 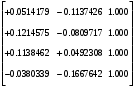 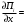 (∆ (∆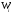 ) / (∆ ) / (∆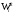 +∆ +∆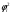 ) )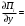 – (∆ – (∆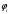 ) / (∆ ) / (∆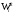 +∆ +∆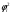 ) )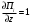 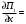 +3.3/( +3.3/(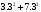 ) = 3.3/(10.89+53.29) = 3.3/64.18 = 0.0514179 ) = 3.3/(10.89+53.29) = 3.3/64.18 = 0.0514179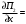 +5.7/( +5.7/(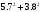 ) = 5.7/(32.49+14.44) = 5.7/46.93 =0.121457489 ) = 5.7/(32.49+14.44) = 5.7/46.93 =0.121457489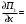 +7.4/( +7.4/(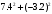 ) = 7.4/(54.76+10.24) = 7.4/65.00 =0.113846153 ) = 7.4/(54.76+10.24) = 7.4/65.00 =0.113846153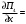 –1.3/( –1.3/(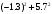 ) = –1.3/(1.69+32.49) = –1.3/34.18 =–0.038033937 ) = –1.3/(1.69+32.49) = –1.3/34.18 =–0.038033937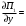 –7.3/( –7.3/(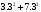 )=–7.3/(10.89+53.29) =–7.3/64.18=–0.113742598 )=–7.3/(10.89+53.29) =–7.3/64.18=–0.113742598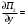 –3.8/( –3.8/(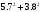 )=–3.8/(32.49+14.44)= –3.8/46.93=–0.080971659 )=–3.8/(32.49+14.44)= –3.8/46.93=–0.080971659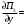 +3.2/( +3.2/(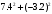 )=3.2/(54.76+10.24)=3.2/65.00=0.049230769 )=3.2/(54.76+10.24)=3.2/65.00=0.049230769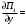 –5.7/( –5.7/(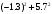 )=–5.7/(1.69+32.49)= –5.7/34.18=–0.166764189 )=–5.7/(1.69+32.49)= –5.7/34.18=–0.166764189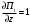 ; ; 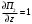 ; ; 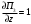 ; ; 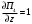 . .1.1.3 Расчёт весовой матрицы 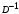 : :Весовой элемент: 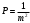 = =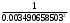 = =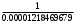 =82070.15875 =82070.15875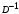 = = 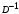 = = 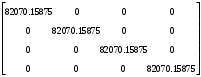 1.1.4 Расчёт промежуточной матрицы 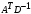 : : 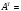 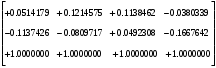 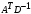 = = 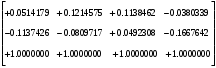 × ×× 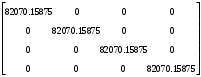 = == 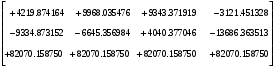 1.1.5 Расчёт матрицы коэффициентов нормального уравнения 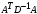 : : 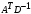 = =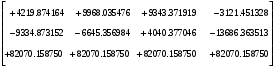 × ×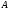 = == 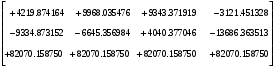 × ×× 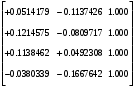 = == 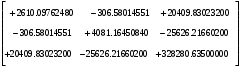 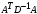 = =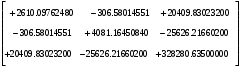 Для обращения матрицы 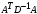 (по аналогии с заданием №1) вычисляем определитель. (по аналогии с заданием №1) вычисляем определитель.Правило Саррюса для расчёта определителя: 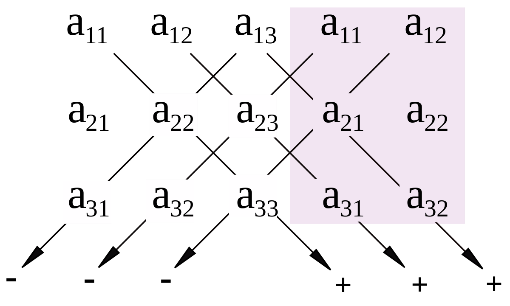 Det( 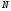 )= )=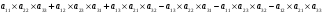 Det( 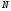 )=372653511870 )=3726535118701.1.6 Расчёт ковариационной матрицы погрешностей географических координат: 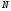 = =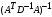 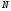 = = 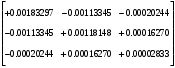 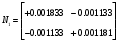 верхний левый блок 1.1.7 Расчёт псевдообратной матрицы 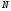 × ×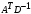 : :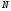 × ×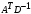 = =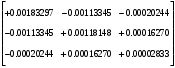 × ×× 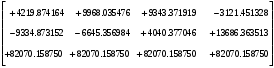 = == 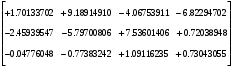 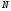 × × 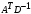 = = 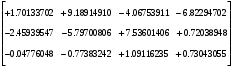 1.1.8 Расчёт вектора искомых неизвестных 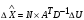 : :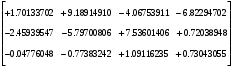 × ×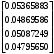 = =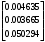 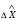 = =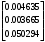 → вектор решений → вектор решений∆ 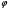 → ∆ 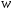 ∆ 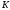 ∆ 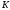 = 0.050294×180/ = 0.050294×180/ =2.8816° =2.8816°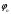 = =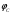 +∆ +∆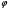 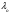 = =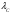 +∆ +∆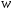 / cos60°= / cos60°=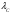 +∆ +∆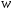 /0.5= /0.5=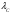 +2×∆ +2×∆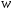
|