2 Теория вероятности. Вероятности событий
 Скачать 493.69 Kb. Скачать 493.69 Kb.
|
|
Пример 6. Найти вероятность, что при одном бросании игральной кости выпадет число очков, кратное двум. ▼ Пусть А – искомое событие. Исходы: {1, 2, 3, 4, 5, 6}, n = 6. Благоприятные: А = {2, 4, 6 }, m = 3. Тогда 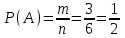 = 0,5. = 0,5.Ответ: 0,5.▲ Задание. Найти вероятность, что при одном бросании игральной кости выпадет число очков, кратное трем. ▼ Пусть А – искомое событие. Исходы: {1, 2, 3, 4, 5, 6}, n = 6. Благоприятные: А = {3, 6 }, m = 2. Тогда  ≈ 0,33. ≈ 0,33.Ответ: ≈ 0,33.▲ Задание. Таня и Маша бросают кубик по одному разу. Выигрывает тот, кто выбросил больше очков. Если количество очков совпадает, это ничья. Найдите вероятность того, что Маша проиграла, если в сумме у них выпало 8 очков. ▼ Составим таблицу всех возможных исходов
Исходы: (2, 6), (3, 5), (4, 4), (5, 3), (6, 2), n = 5. Благоприятные: (5, 3), (6, 2), m = 2. Вероятность, что Маша проиграла: 2/5 = 0,4. Ответ: 0,4. ▲ Задание. Галя дважды бросила игральный кубик. Известно, что в сумме у неё выпало 9 очков. Найдите вероятность, что при втором бросании выпало 6 очков. ▼ Составим таблицу всех возможных исходов
Исходы: (3, 6), (4, 5), (5, 4), (6, 3), n = 4. Благоприятные: (3, 6), m = 1. Искомая вероятность: 1/4 = 0,25. Ответ: 0,25. ▲ Задание. Какова вероятность, что сумма очков, выпавших на двух брошенных костях, равно 5. ▼ Пусть А – искомое событие. Составим таблицу
Общее число исходов n = 62 = 36. Благоприятные: А = {(1, 4), (2, 3), (3, 2), (4, 1) }, m = 4. Тогда 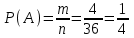 = 0,25. = 0,25.Ответ: 0,25.▲ Задание. Дважды бросается игральный кубик. Какова вероятность того что оба раза выпадет число 5. ▼ Пусть А – искомое событие. Составим таблицу
Общее число исходов n = 62 = 36. Благоприятные: А = {(5, 5)}, m = 1. Тогда 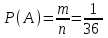 ≈ 0,028. ≈ 0,028.Ответ: ≈ 0,028.▲ Пример 7. Из множества натуральных чисел от 10 до 19 выбирают одно число. Какова вероятность, что оно делится на 3? ▼ Выпишем в ряд заданные числа и отметим те из них, которые делятся на 3: 10, 11, 12, 13, 14, 15, 16, 17, 18, 19. Получили, что из n = (19 – 10 + 1) = 10 заданных чисел на 3 делятся m = 3 числа. Тогда  = 0,3. = 0,3.Ответ: 0,3. ▲ Замечание. На 3 делится каждое третье число в натуральном ряде, на 4 – каждое четвертое, на 5 – каждое пятое, и т.д. Задание. Из множества натуральных чисел от 107 до 198 выбирают одно число. Какова вероятность, что оно делится на 3? ▼ Определим количество групп из трех чисел на участке от 107 до 198. На этом участке всего n = (198 – 107 + 1) = 92 числа. Они составляют 30 полных групп и одну неполную (92/3 = 30 целых и 2 в остатке). В каждой полной группе есть одно число, которое делится на 3. В неполной группе, которую составляют два последних числа, 197 не делится на 3, а 198 делится. Итого, благоприятствующих чисел m = 30 +1 = 31. Тогда 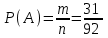 ≈ 0,337. ≈ 0,337.Ответ: ≈ 0,337. ▲ Задание. Коля выбирает трехзначное число. Найдите вероятность того, что оно делится на 5. ▼ Событие А – выбранное число делится на 5. Всего трехзначных чисел n = 999 – 100 + 1 = 900. На пять делится каждое пятое их них, т.е. таких чисел m = 900:5=180. Тогда 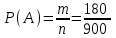 = 0,2. = 0,2.Ответ: 0,2. ▲ Задание. Ответ: 0,25Ответ: 0,75Ответ: 0,052929Для экзамена подготовили билеты с номерами от 1 до 50. Какова вероятность того, что наугад взятый учеником билет имеет однозначный номер? ▼ Событие А – взятый билет имеет однозначный номер. Всего было подготовлено n = 50 билетов, среди которых m = 9 были однозначными. Тогда  = 0,18. = 0,18.Ответ: 0,18. ▲ Пример 8. В классе 26 учащихся, среди них два друга - Сергей и Андрей. Учащихся случайным образом разбивают на 2 равные группы. Найдите вероятность того, что Сергей и Андрей окажутся в одной группе. ▼ Событие А – Сергей и Андрей окажутся в одной группе. Если Сергею первому досталось некоторое место, то Андрею остаётся n = 25 мест. Из них m= 12 - в той же группе, где Сергей. Искомая вероятность  = 0,48. = 0,48.Ответ: 0,48. ▲ Задание. В классе 21 учащихся, среди них два друга - Вадим и Олег. Класс случайным образом разбивают на 3 равные группы. Найдите вероятность того, что Вадим и Олег окажутся в одной группе. ▼ Событие А – Вадим и Олег окажутся в одной группе. Если Вадиму первому досталось некоторое место, то Олегу остаётся n = 20 мест. Из них m= 6 - в той же группе, где Вадим. Искомая вероятность 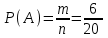 = 0,3. = 0,3.Ответ: 0,3. ▲ Задание. В классе 21 учащийся, среди них две подруги - Аня и Нина. Класс случайным образом делят на семь групп, по 3 человека в каждой. Найдите вероятность того, что Аня и Нина окажутся в одной группе. ▼ Событие А – Аня и Нина окажутся в одной группе. Если Ане первой досталось некоторое место, то Нине остаётся n = 20 мест. Из них m= 2 - в той же группе, где Аня. Искомая вероятность  = 0,1. = 0,1.Ответ: 0,1. ▲ Задание. В классе 16 учащихся, среди них два друга - Вадим и Сергей. Учащихся случайным образом разбивают на 4 равные группы. Найдите вероятность того, что Вадим и Сергей окажутся в одной группе. ▼ Событие А – Вадим и Сергей окажутся в одной группе. Если Вадиму первому досталось некоторое место, то Сергею остаётся n = 15 мест. Из них m= 3 - в той же группе, где Вадим. Искомая вероятность 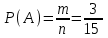 = 0,2. = 0,2.Ответ: 0,2. ▲ Задание. На турнир по шахматам прибыло 26 участников в том числе Коля и Толя. Для проведения жеребьевки первого тура участников случайным образом разбили на две группы по 13 человек. Найти вероятность того, что Коля и Толя попадут в разные группы. ▼ Событие А – Коля и Толя попадут в разные группы. Всего 26 мест. Пусть Коля займет случайное место в любой группе. Останется n = 25 мест, из них в другой группе 13, в которую должен попасть Толя. Следовательно, число благоприятствующих событию А исходов m = 13. Тогда  = 0,52. = 0,52.Ответ: 0,52. ▲ Жеребьевка. Если в условии задачи сказано, что порядок определяется жребием в случайном порядке, то совершенно не важно, каким по счету должен выступать спортсмен (первым, последним или пятым). Пример 9. В чемпионате участвуют 20 спортсменок: 8 из России, 7 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая. ▼ Событие А – первой выступает гимнастка из Китая. Всего спортсменок n = 20. Благоприятствующих событию А исходов m = 5. Тогда 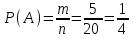 = 0,25. = 0,25.Ответ: 0,25.▲ Задание. В соревнованиях по толканию ядра участвуют 4 спортсмена из Финляндии, 7 спортсменов из Дании, 9 спортсменов из Швеции и 5 – из Норвегии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Швеции. ▼ Событие А – последним выступает спортсмен из Швеции. Всего спортсменов n = 25. Благоприятствующих событию А исходов m = 9. Тогда  = 0,36. = 0,36.Ответ: 0,36. ▲ Задание. На чемпионате по прыжкам в воду выступают 25 спортсменов, среди них 8 прыгунов из России и 9 прыгунов из Парагвая. Порядок выступлений определяется жеребьёвкой. Найдите вероятность того, что шестым будет выступать прыгун из Парагвая. ▼ Событие А – шестым выступает прыгун из Парагвая. Всего спортсменов n = 25. Благоприятствующих событию А исходов m = 9. Тогда  = 0,36. = 0,36.Ответ: 0,36. ▲ Задание. Конкурс исполнителей проводится в 5 дней. Всего заявлено 80 выступлений – по одному от каждой страны. В первый день заявлено 8 выступлений, остальные распределены поровну между оставшимися днями. Порядок выступлений определяется жеребьёвкой. Какова вероятность, что выступление представителя России состоится в третий день конкурса? ▼ Событие А – выступление представителя России состоится в третий день. Всего n = 80 выступлений. В первый день 8 выступлений, в оставшиеся 5 – 1 = 4 дня по (80 – 8)/4 = 18 выступлений. Значит в третий день состоится 18 выступлений. Благоприятствующих событию А исходов m = 18. Тогда  = 0,225. = 0,225.Ответ: 0,225. ▲ Задание. Научная конференция проводится в 5 дней. Всего запланировано 75 докладов: первые три дня по 17 докладов, остальные распределены поровну между четвертым и пятым днями. Порядок докладов определяется жеребьёвкой. Какова вероятность, что доклад профессора М. окажется запланированным на последний день конференции? ▼ Событие А – доклад профессора М на последнем дне. Всего n = 75 докладов. В первый три дня по 17 докладов, в оставшиеся 5 – 3 = 2 дня по (75 – 51)/2 = 12 докладов. Значит в последний день состоится 12 докладов. Благоприятствующих событию А исходов m = 12. Тогда 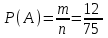 = 0,16. = 0,16.Ответ: 0,16. ▲ Задание. Перед началом первого тура чемпионата по бадминтону участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 26 бадминтонистов, среди которых 10 участников из России, в том числе Руслан Орлов. Найдите вероятность того, что в первом туре Руслан Орлов будет играть с каким-либо бадминтонистом из России? ▼ Событие А – Руслан Орлов будет играть с бадминтонистом из России. Соревнования по бадминтону обычно проводятся с выбыванием, и только в первом туре участвуют все 26 бадминтонистов. Но число всех возможных исходов не равно 26, n = 26 – 1 = 25, потому что Руслан Орлов не может играть с самим собой. По той же причине m = 10 – 1 = 9, ведь Руслан Орлов входит в число 10 участников. Тогда  = 0,36. = 0,36.Ответ: 0,36. ▲ Задание. Перед началом первого тура чемпионата по настольному теннису участников разбивают на игровые пары случайным образом с помощью жребия. Всего в чемпионате участвует 16 спортсменов, среди которых 7 участников из России, в том числе Платон Карпов. Найдите вероятность того, что в первом туре Платон Карпов будет играть с каким-либо спортсменом из России? ▼ Событие А – Платон Карпов будет играть с каким-либо спортсменом из России. Но число всех возможных исходов не равно 16, n = 16 – 1 = 15, потому что Платон Карпов не может играть с самим собой. По той же причине m = 7 – 1 = 6, ведь Платон Карпов входит в число 7 участников. Тогда  = 0,4. = 0,4.Ответ: 0,4. ▲ Задание. В чемпионате мира участвуют 16 команд. С помощью жребия их нужно разделить на четыре группы по четыре команды в каждой. В ящике вперемешку лежат карточки с номерами групп: 1, 1, 1, 1, 2, 2, 2, 2, 3, 3, 3, 3, 4, 4, 4, 4. Капитаны команд тянут по одной карточке. Какова вероятность того, что команда России окажется во второй группе? ▼ Событие А – команда России во второй группе. Общее число исходов n = 16 (16 карточек). Число благоприятствующих событию А исходов m = 4 (четыре карточки с номером 2). Тогда  = 0,25. = 0,25.Ответ: 0,25. ▲ Задачи на теоремы о вероятностях событий Теорема произведения независимых событий Пример 10. Вероятность того, что батарейка бракованная, равна 0,06. Покупатель в магазине выбирает случайную упаковку, в которой две таких батарейки. Найдите вероятность того, что обе батарейки окажутся исправными. ▼ Пусть А, В – события, что соответствующая батарейка исправна. По условию Р(А) = Р(В) = 1 - 0,06 = 0,94. События А, В – независимые. Тогда вероятность, что обе батарейки окажутся исправными 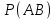 = = 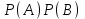 = 0,94∙0,94 = 0,8836. = 0,94∙0,94 = 0,8836.Ответ: 0,8836. ▲ Задание. Вероятность того, что ручка бракованная, равна 0,05. Покупатель в магазине приобретает случайную упаковку, которая содержит две ручки. Найдите вероятность того, что обе ручки в этой упаковке окажутся исправными. ▼ События А, В – соответствующая ручка исправная. По условию P(A) = P(B) = 1- 0,05 = 0.95. События А, В – независимые. Тогда вероятность, что обе ручки исправные P(AB) = P(A)⋅P(B) = 0,95⋅0,95= 0,9025. Ответ: 0,9025▲ Задание. Вероятность того, что аккумулятор не заряжен, равна 0,15. Покупатель в магазине приобретает случайную упаковку, которая содержит два таких аккумулятора. Найдите вероятность того, что оба аккумулятора в этой упаковке окажутся заряжены. ▼ События А, В – соответствующий аккумулятор заряжен. По условию P(A) = P(B) = 1- 0,15 = 0.85. События А, В – независимые. Тогда вероятность, что оба аккумулятора в этой упаковке окажутся заряжены P(AB) = P(A)⋅P(B) = 0,85⋅0,85= 0,7225. Ответ: 0,7225▲ Задание. Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами? ▼ Пусть А, В – события, что на одном из требуемых мест окажется чётное число. По условию Р(А) = Р(В) = 0,5. События А, В – независимые. Тогда вероятность того, что на двух местах одновременно окажутся два чётных числа 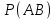 = = 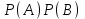 = 0,5∙0,5 = 0,25. = 0,5∙0,5 = 0,25.Ответ: 0,25. ▲ |
