2 Теория вероятности. Вероятности событий
 Скачать 493.69 Kb.
|
|
Задание. Агрофирма закупает куриные яйца в двух домашних хозяйствах. 40% яиц из первого хозяйства - яйца высшей категории, а из второго хозяйства - 20% яиц высшей категории. Всего высшую категорию получает 35% яиц. Найдите вероятность того, что яйцо, купленное у этой агрофирмы, окажется из первого хозяйства. ▼ Пусть х – доля купленных яиц из первого хозяйства. Строим таблицу:
Составим уравнение 0,4∙х + 0,2∙(1 - х) = 0,35∙1 х = 0,75, или 75%. Ответ: 75. ▲ Задание. Автоматическая линия изготавливает батарейки. Вероятность того, что готовая батарейка неисправна, равна 0,02. Перед упаковкой каждая батарейка проходит систему контроля. Вероятность того, что система забракует неисправную батарейку, равна 0,99. Вероятность того, что система по ошибке забракует исправную батарейку, равна 0,01. Найдите вероятность того, что случайно выбранная батарейка будет забракована системой контроля. ▼ Ситуация, при которой батарейка будет забракована, может сложиться в результате событий: A = батарейка действительно неисправна и забракована справедливо или В = батарейка исправна, но по ошибке забракована. Это несовместные события, вероятность их суммы равна сумме вероятностей этих событий. Имеем: 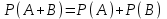 = 0,02∙0,99 + 0,98∙0,01 = 0,0296.Ответ: 0,0296. ▲ Задание. Пенсионер гуляет по дорожкам парка. На каждой развилке он наудачу выбирает следующую дорожку, не возвращаясь обратно. Схема дорожек показано на рисунке. Найти вероятность, что он придет в точку D?
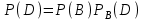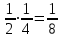▼  =  =0,125.Ответ: 0,125. ▲ Задачи на комбинаторику. Основные правила комбинаторики – это правило суммы и правило произведения. Правило суммы. Если некоторый элемент А можно выбрать n способами, а элемент В можно выбрать m способами, то выбор «либо А, либо В» можно сделать n + m способами. Например, Если на тарелке лежат 5 яблок и 6 груш, то один плод можно выбрать 5 + 6 = 11 способами. Правило произведения. Если элемент А можно выбрать n способами, а элемент В можно выбрать mспособами, то пару А и В можно выбрать nm способами. Например, если есть 2 разных конверта и 3 разные марки, то выбрать конверт и марку можно 6 способами (2∙3 = 6). Произведение всех натуральных чисел от 1 до n включительно называется n – факториалом и обозначается символом n! По определению n! = 1∙2∙3…∙n, причем 0! = 1. Например, если есть 3 шарика – красный, синий и зелёный, то выложить их в ряд можно 6 способами (3∙2∙1 = 3! = 6). Пример 16. Малыш, не умеющий читать, играет с тремя карточками разрезной азбуки «и», «м», «р». Найти вероятность, что используя все карточки, он выложит слово «мир». ▼ Рассмотрим три клетки:
Первой клеткой можем быть одна их букв «и», «м», «р», поэтому первую клетку можно заполнить тремя способами. Поскольку буквы не повторяются, то вторую клетку можно заполнить двумя способами, а третью – одним. Согласно правилу произведения – общее число всех равновозможных исходов n= 3∙2∙1 = 3! = 6, и только в одном m = 1 из них слово «мир». Тогда 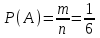 ≈ 0,17.Ответ: ≈ 0,17. ▲ Задание. Малыш, не умеющий читать, играет с тремя карточками разрезной азбуки «о», «к», «к». Найти вероятность, что используя все карточки, он выложит слово «кок». ▼ Число всех исходов 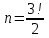 = 3, число благоприятствующих исходов m = 1. 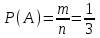Тогда ≈ 0,33.Ответ: ≈ 0,33. ▲ Задание. Малыш, не умеющий читать, играет с четырьмя карточками разрезной азбуки «т», «с», «о», «л». Найти вероятность, что используя все карточки, он выложит слово «стол». ▼ Число всех исходов n= 4! = 24, и только в одном m = 1 их них слово «стол». Тогда 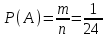 ≈ 0,04.Ответ: ≈ 0,04. ▲ Задание. Малыш, не умеющий читать, играет с четырьмя карточками разрезной азбуки «а», «м», «м», «а». Найти вероятность, что используя все карточки, он выложит слово «мама». ▼ Число всех исходов 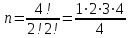 = 6, число благоприятствующих исходов m = 1. 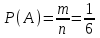Тогда ≈ 0,17.Ответ: ≈ 0,17. ▲ |
