2 Теория вероятности. Вероятности событий
 Скачать 493.69 Kb. Скачать 493.69 Kb.
|
|
Задание. Ответ: 0,156 В магазине три продавца. Каждый из них занят с клиентом с вероятностью 0,3. Найдите вероятность того, что в случайный момент времени все три продавца заняты одновременно (считайте, что клиенты заходят независимо друг от друга). ▼ Пусть А1, А2, А3 – события, что соответствующий продавец занят. По условию, Р(А1) = Р(А2) = Р(А3) = 0,3. События А1, А2, А3 – независимые. Тогда вероятность того, что все три продавца заняты одновременно 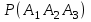 = = 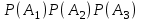 = (0,3)3 = 0,027. = (0,3)3 = 0,027.Ответ: 0,027. ▲ Задание . Ответ: 0,88 Ответ: 0,75 Ответ: 0,2 61616661.66Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть два матча - с командой В и с командой С. Найдите вероятность того, что в обоих матчах первой мячом будет владеть команда А. ▼ Вероятность того, что команда А будет первая владеть мячом в одном матче составляет 1/2, а в двух матчах: (1/2)2 = 0,25. Ответ: 0,25. ▲ Задание. Ответ: 0,88 Ответ: 0,75 Ответ: 0,2 61616661.66Перед началом футбольного матча судья бросает монетку, чтобы определить, какая из команд будет первой владеть мячом. Команда А должна сыграть три матча - с командой В, с командой С и с командой D. Найдите вероятность того, что во всех матчах первой мячом будет владеть команда А. ▼ Вероятность того, что команда А будет первая владеть мячом в одном матче составляет 1/2, а в трех матчах: (1/2)3 = 0,125. Ответ: 0,125. ▲ Задание. Биатлонист пять раз стреляет по мишеням. Вероятность попадания в мишень при одном выстреле равна 0,8. Найдите вероятность того, что биатлонист первые три раза попал в мишени, а последние два промахнулся. Результат округлите до сотых. ▼ Событие А - биатлонист попал в мишень. По условию, вероятность попадания Р(А) = 0,8, тогда вероятность промахнуться Р( 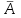 ) = 0,2. События попасть или промахнуться при каждом выстреле независимы. Тогда ) = 0,2. События попасть или промахнуться при каждом выстреле независимы. Тогда = 0,8∙0,8∙0,8∙0,2∙0,2 = 0,02048. = 0,8∙0,8∙0,8∙0,2∙0,2 = 0,02048.Ответ: 0,02. ▲ Задание. Если шахматист А. играет белыми фигурами, то он выигрывает у шахматиста Б. с вероятностью 0,5. Если А. играет черными, то А. выигрывает у Б. с вероятностью 0,3. Шахматисты А. и Б. играют две партии, причём во второй партии меняют цвет фигур. Найдите вероятность того, что А. выиграет оба раза. ▼ Возможность выиграть первую и вторую партию не зависят друг от друга. Вероятность произведения независимых событий равна произведению их вероятностей: 0,5·0,3 = 0,15. Ответ: 0,15. ▲ Теорема сложения несовместных событий Пример 11. В ящике лежат 10 шаров: 4 красных, 1 синий и 5 черных. Наугад вынимается один шар. Какова вероятность того, что шар красный или синий. ▼ Пусть А, В – события, что вынут красный или синий шар соответственно. Вероятности: P(A) = 4/10 = 0,4; P(В) = 1/10 = 0,1. События А, В – несовместные. Тогда вероятность того, что вынутый шар красный или синий равна P(A + B) = P(A) + P(В) = 0,4 + 0,1= 0,5. Ответ: 0,5. ▲ Задание. На экзамене по геометрии школьник отвечает на один вопрос из списка экзаменационных вопросов. Вероятность того, что это вопрос по теме «Вписанная окружность», равна 0,2. Вероятность того, что это вопрос по теме «Параллелограмм», равна 0,15. Вопросов, которые одновременно относятся к этим двум темам, нет. Найдите вероятность того, что на экзамене школьнику достанется вопрос по одной из этих двух тем. ▼ Вероятность суммы двух несовместных событий равна сумме вероятностей этих событий: 0,2 + 0,15 = 0,35. Ответ: 0,35. ▲ Задание. Вероятность того, что новый электрический чайник прослужит больше года, равна 0,93. Вероятность того, что он прослужит больше двух лет, равна 0,87. Найдите вероятность того, что он прослужит меньше двух лет, но больше года. ▼ Пусть A = «чайник прослужит больше года, но меньше двух лет», В = «чайник прослужит больше двух лет», С = «чайник прослужит ровно два года», тогда A + B + С = «чайник прослужит больше года». События A, В и С несовместные, вероятность их суммы равна сумме вероятностей этих событий. Вероятность события С, состоящего в том, что чайник выйдет из строя ровно через два года — строго в тот же день, час и секунду - равна нулю. Тогда P(A + B+ С) = P(A) + P(B) + P(С)= P(A) + P(B), откуда, используя данные из условия, получаем 0,93 = P(A) + 0,87. Тем самым, для искомой вероятности имеем: P(A) = 0,93 − 0,87 = 0,06. Ответ: 0,06. ▲ Задание. Из районного центра в деревню ежедневно ходит автобус. Вероятность того, что в понедельник в автобусе окажется меньше 20 пассажиров, равна 0,94. Вероятность того, что окажется меньше 15 пассажиров, равна 0,56. Найдите вероятность того, что число пассажиров будет от 15 до 19. ▼ Рассмотрим события A = «в автобусе меньше 15 пассажиров» и В = «в автобусе от 15 до 19 пассажиров». Их сумма - событие A + B = «в автобусе меньше 20 пассажиров». События A и В несовместные, вероятность их суммы равна сумме вероятностей этих событий P(A + B) = P(A) + P(B), откуда, используя данные из условия, получаем 0,94 = 0,56 + P(В). Тем самым, для искомой вероятности имеем: P(В) = 0,94 − 0,56 = 0,38. Ответ: 0,38. ▲ Задание. Ответ: 0,Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,7. Найдите вероятность того, что мишень будет поражена (либо первым, либо вторым выстрелом). ▼ Пусть A - событие, что мишень поражена стрелком с первого выстрела, B - событие, что мишень поражена со второго выстрела. Вероятность P(A) = 0,7. Событие B наступает, если, стреляя первый раз, стрелок промахнулся, а, стреляя второй раз, попал. Это независимые события, их вероятность равна произведению вероятностей этих событий: P(B) = 0,3·0,7 = 0,21. События A и B несовместные, вероятность их суммы равна сумме вероятностей этих событий: P(A + B) = P(A) + P(B) = 0,7 + 0,21 = 0,91. Ответ: 0,91. ▲ Теорема сложения несовместных событий (хотя бы одно) Пример 12. В магазине стоят два платёжных автомата. Каждый из них может быть неисправен с вероятностью 0,05 независимо от другого автомата. Найдите вероятность того, что хотя бы один автомат исправен. ▼ Пусть А1, А2 – события, что соответствующая автомат исправен. По условию, Р( 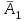 ) = Р( ) = Р( ) = 0,05. События ) = 0,05. События 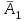 , , – независимые, тогда – независимые, тогдаСобытия А1+ А2 и 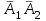 - противоположные. Тогда вероятность того, что хотя бы один автомат исправен - противоположные. Тогда вероятность того, что хотя бы один автомат исправен =1 - =1 - = 1 - 0,0025 = 0,9975. = 1 - 0,0025 = 0,9975.Ответ: 0,9975. ▲ Задание. Ответ: 0,02 3333Помещение освещается фонарём с двумя лампами. Вероятность перегорания лампы в течение года равна 0,3. Найдите вероятность того, что в течение года хотя бы одна лампа не перегорит. ▼ Пусть А1, А2 – события, что в течение года соответствующая лампа не перегорит. По условию, Р( 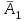 ) = Р( ) = Р( ) = 0,3. События ) = 0,3. События 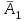 , , – независимые, тогда – независимые, тогда = = = 0,3∙0,3 = 0,09. = 0,3∙0,3 = 0,09.События А1+ А2 и 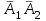 - противоположные. Тогда вероятность того, что в течение года хотя бы одна лампа не перегорит. - противоположные. Тогда вероятность того, что в течение года хотя бы одна лампа не перегорит. =1 - =1 - = 1 - 0,09 = 0,91. = 1 - 0,09 = 0,91.Ответ: 0,91. ▲ Задание. В торговом центре два одинаковых автомата продают кофе. Вероятность того, что к концу дня в автомате закончится кофе, равна 0,3. Вероятность того, что кофе закончится в обоих автоматах, равна 0,12. Найдите вероятность того, что к концу дня кофе останется в обоих автоматах. ▼ Пусть А, В - события, что кофе закончится в соответствующем автомате. По условию: Р(А) = Р(В) = 0,3, Р(АВ) = 0,12. Вероятность, что кофе закончится хотя бы в одном из автоматов равна сумме вероятностей наступления этих событий без вероятности их совместного наступления: P(A + B) = P(A) + P(B) − P(AB) = 0,3 + 0,3 - 0,12 = 0,48. Вероятность, что кофе останется в обоих автоматах: Р( 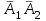 ) = 1 - P(A + B) = 1 – 0,48 = 0,52. ) = 1 - P(A + B) = 1 – 0,48 = 0,52.Ответ: 0,52. ▲ До первого выстрела Пример 13. Стрелок стреляет по мишени один раз. В случае промаха стрелок делает второй выстрел по той же мишени. Вероятность попасть в мишень при одном выстреле равна 0,6. Найти вероятность, что мишень будет поражена одним выстрелом. ▼ Пусть события А1, А2 - попадание в цель при соответствующем выстреле. По условию Р(А1) = Р(А2) = 0,6. Вероятность промаха при первом выстреле: Р( 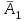 ) = 1 – 0,6 = 0,4. Если цель не будет поражена при первом выстреле, то делаем второй выстрел. Вероятность попадания при втором выстреле, если промахнулись в первом: Р( ) = 1 – 0,6 = 0,4. Если цель не будет поражена при первом выстреле, то делаем второй выстрел. Вероятность попадания при втором выстреле, если промахнулись в первом: Р( ) = 0,4∙0,6 = 0,24. Вероятность попадания при первом или втором выстреле: Р( ) = 0,4∙0,6 = 0,24. Вероятность попадания при первом или втором выстреле: Р( ) = 0,6 + 0,24 = 0,84. ) = 0,6 + 0,24 = 0,84.Ответ: 0,84. ▲ Задание. При артиллерийской стрельбе автоматическая система делает выстрел по цели. Если цель не уничтожена, то система делает повторный вы-стрел. Выстрелы повторяются до тех пор, пока цель не будет уничтожена. Вероятность уничтожения некоторой цели при первом выстреле равна 0,4, а при каждом последующем - 0,6. Сколько выстрелов потребуется для того, чтобы вероятность уничтожения цели была не менее 0,90? ▼ Пусть события А1, А2, А3,… - попадание в цель при соответствующем выстреле. По условию Р(А1) = 0,4; Р(А2) = Р(А3) =…= 0,6. Будем стрелять до тех пор, пока вероятность попадания не станет удовлетворять условию. Вероятность попадания при первом выстреле: Р(А1) = 0,4 < 0,90, т.е. необходимо делать второй выстрел. А при каком условии мы стреляем повторно? Вероятность попадания при втором выстреле, если промахнулись в первом: Р(  ) = 0,6∙0,6 = 0,36. Вероятность попадания при первом или втором выстреле Р( ) = 0,6∙0,6 = 0,36. Вероятность попадания при первом или втором выстреле Р( ) = 0,4 + 0,36 = 0,76 < 0,90, т.е. необходимо делать третий выстрел. ) = 0,4 + 0,36 = 0,76 < 0,90, т.е. необходимо делать третий выстрел.Вероятность попадания при третьем выстреле, если промахнулись в первых двух: Р( 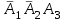 ) = 0,6∙0,4∙0,6 = 0,144. Вероятность попадания при первом, втором или третьем выстреле Р( ) = 0,6∙0,4∙0,6 = 0,144. Вероятность попадания при первом, втором или третьем выстреле Р( ) = 0,76 + 0,144 = 0,904 > 0,90, т.е. третьем выстреле достигли нужной точности. ) = 0,76 + 0,144 = 0,904 > 0,90, т.е. третьем выстреле достигли нужной точности.Таким образом потребовалось 3 выстрела. Ответ: 3. ▲ Формула полной вероятности. Решаются построением таблицы. Пример 14. Офис закупает канцелярию для сотрудников трех различных фирм. Причем, продукция первой фирмы составляет 40% всех поставок, а остальных двух – поровну. Чаще всего приходится закупать пишущие ручки. Опытным путем выяснилось, что 2% ручек второй фирмы – бракованные. Процент брака в первой и третьей фирме составляет 1% и 3% соответственно. Сотрудник с утра взял ручку из новой поставки канцелярии. Найдите вероятность того, что она будет исправна. ▼ Пусть событие А – взятое изделие исправное. Строим таблицу:
Вероятность взять бракованное изделие Р( 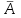 ) = 0,4∙0,01 + 0,3∙0,02 + 0,3∙0,03 = 0,019. ) = 0,4∙0,01 + 0,3∙0,02 + 0,3∙0,03 = 0,019.Вероятность взять исправное изделие Р(А) = 1 – Р(А) = 1 – 0,019 = 0,981. Ответ: 0,981. ▲ Задание. Ответ: 0,52 Две фабрики выпускают одинаковые стекла для автомобильных фар. Первая фабрика выпускает 45% этих стекол, вторая - 55%. Первая фабрика выпускает 3% бракованных стекол, а вторая - 1%. Найдите вероятность того, что случайно купленное в магазине стекло окажется бракованным. ▼ Пусть событие А – купленное стекло окажется бракованным. Строим таблицу:
Вероятность взять бракованное изделие Р(А) = 0,45∙0,03 + 0,55∙0,01 = 0,019. Ответ: 0,019. ▲ Задание. Ответ: 0,52 Два завода выпускают одинаковые предохранители. Первый завод выпускает 40% предохранителей, второй - 60%. Первый завод выпускает 4% бракованных предохранителей, а вторая - 3%. Найдите вероятность, что случайно выбранный в магазине предохранитель окажется бракованным. ▼ Пусть событие А – выбранный в магазине предохранитель окажется бракованным. Строим таблицу:
Вероятность взять бракованное изделие Р(А) = 0,4∙0,04 + 0,6∙0,03 = 0,034. Ответ: 0,034. ▲ |
