Выбор электродвигателя и расчет основных параметров привода

• Название: Выбор электродвигателя и расчет основных параметров привода
• Дата: 13.05.2023
• Размер: 0.86 Mb.
• Имя файла: PZ_oformlennaya.docx
• Тип: Документы; #1126938
• страница: 3 из 13

2.3. Проектный расчет передачи

2.3.1.Межосевое расстояние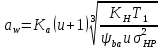



гдеК_а=410 для косозубых передач.

Принимаю коэффициент ширины зубчатого венца для косозубой передачи ψ_ba=0,400.На этапе проектного расчета задаемся значением коэффициента контактной нагрузки K_H=1,2. Тогда: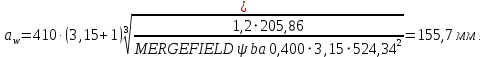



Полученное межосевое расстояние округляю до ближайшего большего стандартного значения a_w=160 мм.

2.3.2.Модуль, числа зубьев колес и коэффициенты смещения

Рекомендуемый диапазон для выбора модуля: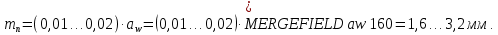



Из полученного диапазона выбираю стандартный модуль m_n =2,5мм.

Суммарное число зубьев передачи:



Полученное значение 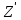округляю до ближайшего целого числа Z_∑ = 125 и определим делительный угол наклона зуба: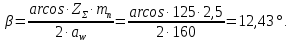



Число зубьев шестерни: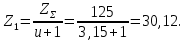



Полученное значение Z₁ округляю до ближайшего целого числа Z₁ =30.

Число зубьев колеса: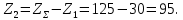



Фактическое передаточное число: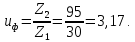



При u<4,5 отличие фактического передаточного числа от номинального должно быть не больше 2,5%.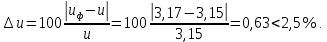



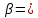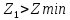Z_min= 17cos³ 15,83, принимаем коэффициент смещения x₁=0 т к , x₂=0

2.3.3.Ширина зубчатых венцов и диаметры колес

Ширина зубчатого венца колеса: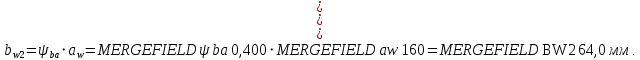



Округляю b_w2 до ближайшего числа из ряда нормальных линейных размеров b_w2=65мм.Ширину зубчатого венца шестерни b_w1 примем b_w1=67мм.

Определим диаметры окружностей зубчатых колес:

-делительные окружности: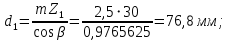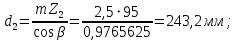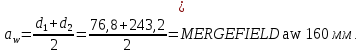







-окружности вершин зубьев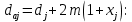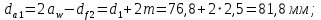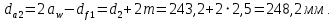





-окружности впадин зубьев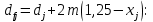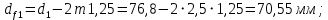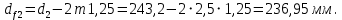





2.3.4.Окружная скорость в зацеплении и степень точности передачи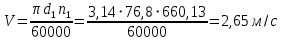



По табл.8 назначаю степень точности передачи n_cт =8

2.4.Проверочный расчет передачи

2.4.1Проверка контактной прочности зубьев

Используем формулу: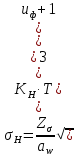



где Z_σ=8400 для косозубых передач.

Коэффициент контактной нагрузки: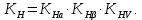



Коэффициент неравномерности распределения нагрузки между зубьями: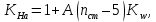



где А=0,15 для косозубых передач,K_w – коэффициент, учитывающий приработку зубьев.

При НВ₂ 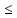350 используем формулу:



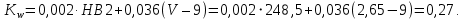Тогда: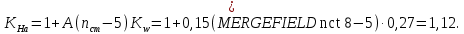



Коэффициент неравномерности распределения нагрузки по ширине колеса: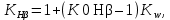



где K⁰_Hβ – коэффициент неравномерности распределения нагрузки в начальный период работы.

Для определения K⁰_Hβнайдем коэффициент ширины венца по диаметру: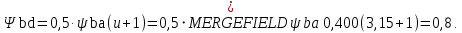



По значению Ψ_bdопределим K⁰_Hβ=1,05.Тогда: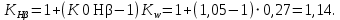



Динамический коэффициент K_HV=1,06 определим методом линейной интерполяции.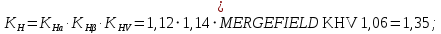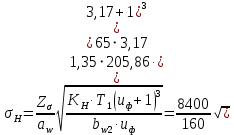





Поскольку , выполним расчет недогрузки по контактным напряжениям:



2.4.2 Проверка изгибной прочности зубьев

Напряжения изгиба в зубе шестерни: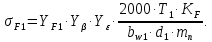



Коэффициент формы зуба при x_j=0: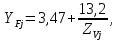



где 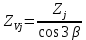– эквивалентное число зубьев.









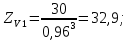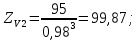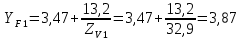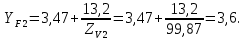Коэффициент, учитывающие влияние угла наклона зуба на его прочность: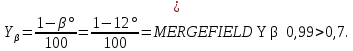



Коэффициент торцевого перекрытия: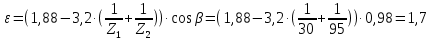



Коэффициент, учитывающие перекрытие зубьев: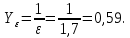



Коэффициент нагрузки при изгибе: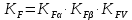



Для определения его коэффициентов используем зависимости: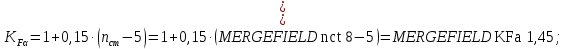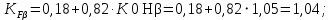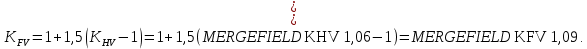







Тогда: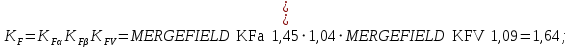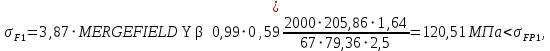



где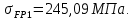

Напряжение в зубьях колеса: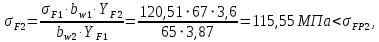



_где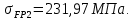