высшая математика 6. Задание № 6. 7.8. Вид ресурсов
 Скачать 89.39 Kb. Скачать 89.39 Kb.
|
|
Задание № 6. Оптимальное планирование. Постановка задачи: предприятие располагает ресурсами сырья, рабочей силы и оборудованием, необходимым для производства любого из трех видов производимых товаров 1, 2, 3. Затраты ресурсов на изготовление единицы товара, а также запасы ресурсов указаны в следующей таблице: Таблица 1
Определить какой ассортимент товара надо выпускать, чтобы прибыль была максимальной, используя следующие данные: 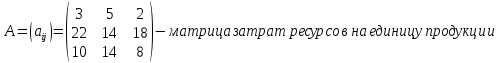 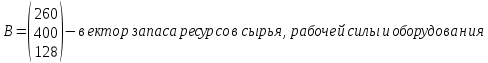 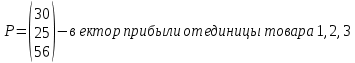  Информацию представить в виде таблицы №1, построить модель. Решить симплексным методом, проанализировать полученный результат. Решение. Исходную информацию представим в виде таблицы №1: Таблица 1
Обозначим х1, х2, х3 – число единиц продукции вида 1, 2 и 3 соответственно, запланированных к производству. Для их изготовления потребуется (3х1 + 5х2 + 2х3) кг. сырья, (22х1 + 14х2 + 18х3) ч. рабочей силы, (10х1 + 14х2 + 8х3) станко-час. оборудования. Потребление ресурсов не должно превышать их запасов, соответственно 260, 400 и 128 единиц. Тогда экономико-математическую модель задачи можно сформулировать так: Найти план выпуска продукции Х = (х1, х2, х3), удовлетворяющий системе ограничений: 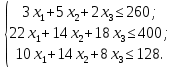 и условию х1, х2, х3 ≥ 0, при котором функция F = 30х1 + 25х2 + 56х3 принимает максимальное значение. Решим прямую задачу линейного программирования симплексным методом, с использованием симплексной таблицы. Для построения первого опорного плана систему неравенств приведем к системе уравнений путем введения дополнительных переменных (переход к канонической форме). В 1-м неравенстве смысла (≤) вводим базисную переменную x4. В 2-м неравенстве смысла (≤) вводим базисную переменную x5. В 3-м неравенстве смысла (≤) вводим базисную переменную x6. 3x1 + 5x2 + 2x3 + x4 = 260 22x1 + 14x2 + 18x3 + x5 = 400 10x1 + 14x2 + 8x3 + x6 = 128 Матрица коэффициентов A = a(ij) этой системы уравнений имеет вид: 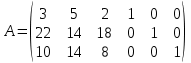 Решим систему уравнений относительно базисных переменных: x4, x5, x6. Полагая, что свободные переменные равны 0, получим первый опорный план: X0 = (0, 0, 0, 260, 400, 128).
Текущий опорный план не оптимален, так как в индексной строке находятся отрицательные коэффициенты. В качестве ведущего выберем столбец, соответствующий переменной x3, так как это наибольший коэффициент по модулю. Вычислим значения Di по строкам как частное от деления: bi/ai3 и из них выберем наименьшее: min (260:2, 400:18, 128:8) = 16. Следовательно, 3-ая строка является ведущей. Разрешающий элемент равен (8) и находится на пересечении ведущего столбца и ведущей строки.
Пересчитаем симплекс-таблицу по правилу прямоугольника. Получаем новую симплекс-таблицу:
Среди значений индексной строки нет отрицательных. Поэтому эта таблица определяет оптимальный план задачи, который можно записать так: x1 = 0, x2 = 0, x3 = 16. F(X) = 30·0 + 25·0 + 56·16 = 896. Анализ оптимального плана. В оптимальный план вошла дополнительная переменная x4. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 1-го вида в количестве 228. В оптимальный план вошла дополнительная переменная x5. Следовательно, при реализации такого плана имеются недоиспользованные ресурсы 2-го вида в количестве 112. Значение 40> 0 в столбце x1 означает, что использование x1 - не выгодно. Значение 73> 0 в столбце x2 означает, что использование x2 - не выгодно. Значение 0 в столбце x3 означает, что использование x3 - выгодно. Задание № 7. Графический метод. Постановка задачи: для изготовления двух видов продукции имеются три вида ресурсов, объемы которых ограничены величинами b1, b2, b3 соответственно. Расход i-го вида ресурса на изготовление одной единицы j-го вида продукции равен aij, i = 1, 2, 3, j = 1, 2. Объем выпуска каждого из видов продукции ограничен число x1* и x2* единиц, прибыль, получаемая от реализации одной единицы изготовленной продукции равна с1 и с2 соответственно. Данные задачи могут быть представлены в форме таблицы:
Требуется составить план выпуска продукции (число единиц продукции по каждому виду), удовлетворяющий принятым ограничениям и приносящий максимум прибыли после реализации выпущенной продукции, имея следующие данные: 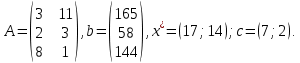 Решение. Исходные данные:
Математическая модель задачи: Обозначим х1, х2 – число единиц продукции вида 1 и 2, запланированных к производству. Для их изготовления потребуется (3х1 + 11х2) единиц ресурса 1, (2х1 + 3х2) единиц ресурса 2, (8х1 + х2) единиц ресурса 3. Потребление ресурсов не должно превышать их запасов, соответственно 165, 58 и 144 единиц. Объем выпуска каждого из видов продукции ограничен 17 и 14 единиц соответственно. Тогда экономико-математическую модель задачи можно сформулировать так: Найти план выпуска продукции Х = (х1, х2), удовлетворяющий системе ограничений: 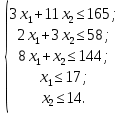 и условию х1, х2 ≥ 0, при котором функция F = 7х1 + 2х2= 0 принимает максимальное значение. Для графического решения задачи построим множество допустимых решений, задаваемое неравенствами-ограничениями (1) – (5): 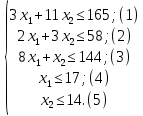 Ограничение (1) в задаче определяется прямой 3x1 + 11x2 = 165, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (1) получается верное неравенство: 3·0 + 11·0 ≤ 165. Ограничение (2) в задаче определяется прямой 2x1 + 3x2 = 58, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (2) получается верное неравенство: 2·0 + 3·0 ≤ 58. Ограничение (3) в задаче определяется прямой 8x1 + x2 = 144, проходящей через точки:
Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 8·0 + 0 ≤ 144. Ограничение (4) в задаче определяется прямой x1 = 17, параллельной оси х2. Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 0 ≤ 17. Ограничение (5) в задаче определяется прямой x2 = 14, параллельной оси х1. Множество допустимых решений в задаче будет ограничено этой прямой, и будет содержать точку (0, 0)Т, так как при подстановке координат этой точки в ограничение (3) получается верное неравенство: 0 ≤ 14. Ограничения х1 ≥ 0, х2 ≥ 0 в задаче задают 1-ю четверть координатной плоскости. Множество допустимых решений включает все точки, в которых ограничения выполняются одновременно. Отметим крайние точки получившегося множества: A, B, С, D, E. П 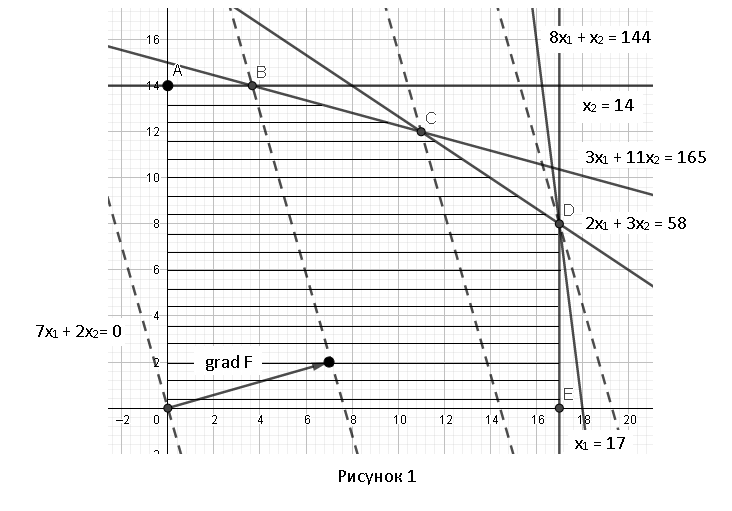 остроим градиент функции f (X) = (7, 2)Т в точке (0, 0)Т. Построим линию уровня функции f (X) = C , проходящую через точку (0, 0)Т. Для этого найдем значение константы C , подставив координаты точки в целевую функцию: C = 7· 0 + 2· 0 = 0, и затем построим прямую 7x1 + 2x2 = 0. Построенная линия уровня перпендикулярна градиенту и пересекает множество допустимых решений. Вектор-градиент, составленный из коэффициентов целевой функции, указывает направление максимизации f(X). Будем двигать эту прямую параллельным образом. Поскольку нас интересует наибольшее значение f(x), поэтому двигаем прямую до последнего касания обозначенной области. Прямая F(x) = const пересекает область в точке D. Так как точка D получена в результате пересечения прямых (3) и (4), то ее координаты удовлетворяют уравнениям этих прямых: 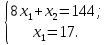 Решив систему уравнений, получим: x1 = 17; x2 = 8. Откуда найдем максимальное значение целевой функции: Fmax (X) = 7·17 + 2·8 = 135. Задание № 8. Транспортная задача. Постановка задачи: на складах А1, А2, А3 имеются запасы продукции в количествах 180, 300, 120 т. соответственно. Потребители В1, В2, В3 должны получить эту продукцию в количествах 110, 350, 140 т. соответственно. Найти такой вариант прикрепления поставщиков к потребителям, при котором сумма затрат на перевозки была бы минимальной. Расходы по перевозке 1 т. продукции заданы матрицей С (ден.ед.) 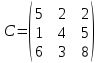 Решение. Стоимость доставки единицы груза из каждого пункта отправления в соответствующие пункты назначения задана матрицей тарифов:
Проверим необходимое и достаточное условие разрешимости задачи. ∑a = 180 + 300 + 120 = 600 ∑b = 110 + 350 + 140 = 600 Условие баланса соблюдается. Запасы равны потребностям. Следовательно, модель транспортной задачи является закрытой. Используя метод наименьшей стоимости, построим первый опорный план транспортной задачи. Искомый элемент равен c21 = 1. Для этого элемента запасы равны 300, потребности 110. Поскольку минимальным является 110, то вычитаем его. x21 = min(300, 110) = 110.
Искомый элемент равен c12 = 2. Для этого элемента запасы равны 180, потребности 350. Поскольку минимальным является 180, то вычитаем его. x12 = min(180, 350) = 180.
Искомый элемент равен c32 = 3. Для этого элемента запасы равны 120, потребности 170. Поскольку минимальным является 120, то вычитаем его. x32 = min(120, 170) = 120.
Искомый элемент равен c22 = 4. Для этого элемента запасы равны 190, потребности 50. Поскольку минимальным является 50, то вычитаем его. x22 = min(190, 50) = 50.
Искомый элемент равен c23 = 5. Для этого элемента запасы равны 140, потребности 140. Поскольку минимальным является 140, то вычитаем его. x23 = min(140, 140) = 140.
В результате получен первый опорный план, который является допустимым, так как все грузы от поставщиков вывезены, потребность потребителей удовлетворена, а план соответствует системе ограничений транспортной задачи.
Число занятых клеток таблицы (должно быть m + n – 1 = 5) 5. Следовательно, опорный план является невырожденным. Значение целевой функции для этого опорного плана равно: F(x) = 2·180 + 1·110 + 4·50 + 5·140 + 3·120 = 1730 Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0. u1 + v2 = 2; 0 + v2 = 2; v2 = 2 u2 + v2 = 4; 2 + u2 = 4; u2 = 2 u2 + v1 = 1; 2 + v1 = 1; v1 = -1 u2 + v3 = 5; 2 + v3 = 5; v3 = 3 u3 + v2 = 3; 2 + u3 = 3; u3 = 1
Опорный план не является оптимальным, так как существуют оценки свободных клеток, для которых ui + vj > cij (1;3): 0 + 3 > 2; ∆13 = 0 + 3 - 2 = 1 > 0 Выбираем максимальную оценку свободной клетки (1;3): 2. Для этого в перспективную клетку (1;3) поставим знак «+», а в остальных вершинах многоугольника чередующиеся знаки «-», «+», «-».
Цикл приведен в таблице (1,3 → 1,2 → 2,2 → 2,3). Из грузов хij стоящих в минусовых клетках, выбираем наименьшее, т.е. у = min (2, 3) = 140. Прибавляем 140 к объемам грузов, стоящих в плюсовых клетках и вычитаем 140 из Хij, стоящих в минусовых клетках. В результате получим новый опорный план.
Проверим оптимальность опорного плана. Найдем предварительные потенциалы ui, vj. по занятым клеткам таблицы, в которых ui + vj = cij, полагая, что u1 = 0. u1 + v2 = 2; 0 + v2 = 2; v2 = 2 u2 + v2 = 4; 2 + u2 = 4; u2 = 2 u2 + v1 = 1; 2 + v1 = 1; v1 = -1 u3 + v2 = 3; 2 + u3 = 3; u3 = 1 u1 + v3 = 2; 0 + v3 = 2; v3 = 2
Опорный план является оптимальным, так все оценки свободных клеток удовлетворяют условию ui + vj ≤ cij. Минимальные затраты составят: F(x) = 2·40 + 2·140 + 1·110 + 4·190 + 3·120 = 1590 Анализ оптимального плана. Из 1-го склада необходимо груз направить 2-му потребителю (40 ед.), 3-ему потребителю (140 ед.) Из 2-го склада необходимо груз направить 1-му потребителю (110 ед.), 2-му потребителю (190 ед.) Из 3-го склада необходимо весь груз направить в 2-му потребителю. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
