Экономико-матмодели. Выделить и формально описать наиболее существенные связи экономических объектов
 Скачать 461.57 Kb. Скачать 461.57 Kb.
|
|
O I/p1 X1 Задача потребительского выбора  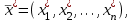 (35) (35)Формальный вид задачи потребительского выбора – ищется точка максимума (35) функции полезности на бюджетном множестве  (36) (36)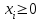 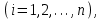 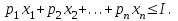 Рассмотрим задачу потребительского выбора для случая набора для двух товаров: найти набор 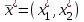 такой что такой чтоПоиск оптимального набора 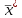 можно интерпретировать графически как последовательный переход на линии безразличия более высокого уровня полезности (рис.4)- вправо-вверх - до тех пор, пока эти линии имеют общие точки с бюджетным множеством. можно интерпретировать графически как последовательный переход на линии безразличия более высокого уровня полезности (рис.4)- вправо-вверх - до тех пор, пока эти линии имеют общие точки с бюджетным множеством. 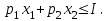 (38) (38)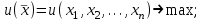 (39) (39) . .Последнее уравнение в (39) называется уравнением связи. Рис. 4 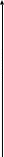 Х2  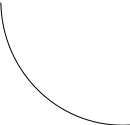  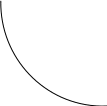    х2 х2  O x2 X1 Решение задачи потребительского выбора Функция Лагранжа 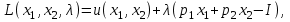 (40) (40)где - неопределенный множитель Ланранжа. Экономический смысл этого множителя: если цены и доход меняются в одно и то же число раз , то функция полезности, а значит, и решение задачи потребительского выбора не изменится. Далее ищется точка максимума функции L: все три частные производные этой функции приравниваются к нулю, т.е. получаем систему трех уравнений:  L / х1 = u1 - p1 = 0, L / х1 = u1 - p1 = 0,L / х2 = u2 - p2 = 0, L / =p1x1 - p2x2 – i = 0. И      сключив из этих уравнений неизвестную , получаем систему двух уравнений с двумя неизвестными x1 и x2 :  (41) (41) Решение (x1*,x2*) системы уравнений (41) является решением задачи потребительского выбора. В многомерном случае (39) также используется метод Лагранжа имеет вид:  (42) Далее, согласно условиям максимума , составляется система из (n+1) уравнений относительно (n+1) неизвестных 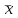 и и 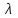 : :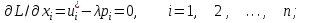 (43) (43) 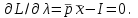 Исключая из этих уравнений неизвестную 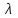 , получаем систему n уравнений относительно n неизвестных – координат точки условного максимума : , получаем систему n уравнений относительно n неизвестных – координат точки условного максимума :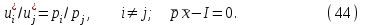 Решение 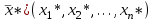 этой системы уравнений – точка условного экстремума - является решением общей задачи потребительского выбора. этой системы уравнений – точка условного экстремума - является решением общей задачи потребительского выбора.Функции спроса Решение задачи потребительского выбора 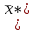 называется точкой спроса. Эта точка спроса зависит от цен называется точкой спроса. Эта точка спроса зависит от цен 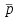 и дохода I. Иными словами, точка спроса является функцией цен и дохода, т.е. функцией спроса. В свою очередь, функция спроса представляет собой вектор-функцию п + 1 аргумента (в общем случае п цен р1, р2,…, рп, и дохода I), состоящую из п компонент: и дохода I. Иными словами, точка спроса является функцией цен и дохода, т.е. функцией спроса. В свою очередь, функция спроса представляет собой вектор-функцию п + 1 аргумента (в общем случае п цен р1, р2,…, рп, и дохода I), состоящую из п компонент:х = х (р1, р2,…, рп, , I), Таким образом, функция спроса – это набор п функций, каждая из которых зависит от п + 1 аргумента: х1 = х1 (р1, р2,…, рп, , I), х2 = х2 (р1, р2,…, рп, , I), ……………………………(45) хп = хп (р1, р2,…, рп, , I. Функции (45) называются функциямиспроса соответствующих товаров. Пример 2. Для набора из двух товаров на рынке, известных ценах на них р1 и р2 и доходе I найти функции спроса, если функция полезности имеет вид u ( x1 , x2 ) = x10,5 x20,5 . Решение. Дифференцируя данную функцию полезности, получаем u1 = 0,5 x20,5 / x10,5, u2 = 0,5 x10,5 / x20,5. Далее, подстановка в формулы (41) приводит к системе уравнений: 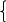 x2 / x1 = p1 / p2 , x2 / x1 = p1 / p2 ,p1 x1 + p2 x2 = I . Из первого уравнения следует, что затраты денежных средств на оба вида товаров должны быть одинаковыми, т.е. p1 x1 = p2 x2 . Следовательно, из второго уравнения получаем, что функции спроса имеют вид: x*1 = I / 2p1 , x*2 = I / 2p2 . Иными словами, в данном случае расход на каждый товар составляет половину дохода потребителя, а количество приобретенного товара равно затраченной на него сумме, поделенной на цену товара. Модель Р. Стоуна Модель потребительского спроса с функцией полезности мультипликативного вида (неоклассическая)  xi > ai , ai > 0, i = 1, 2,,…,n (46) Для приобретения минимального набораа необходимо, чтобы доход был больше стоимости этого набора, т.е. 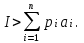 (47) Добавив к целевой функции (46) бюджетные ограничения, получим задачу потребительского выбора (36), называемую моделью Р. Стоуна. Приравняв нулю частные производные функции Лагранжа L по всем переменным, получим систему п + 1 уравнений:  Из соотношений первого вида получаем выражения для неизвестных хi :  (48) у 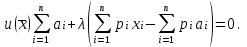 множим каждое из уравнений (48) на λpi и просуммируем их по i ; получаем: Отсюда отношение u (x ) / λ с учетом условия связи имеет вид: 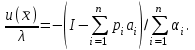 Подставляя это выражение в (26.27), получаем в окончательном виде формулы для функции спроса: 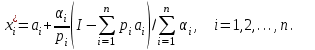 (49) Полученные функции спроса легко интерпретировать по последовательности действий: В начале приобретается набор а необходимых количеств товаров. Затем рассчитывается оставшаяся сумма денег. Это сумма денег распределяется пропорционально весам “ценности” i товаров. Поделив распределенные на приобретение каждого товара суммы денег на соответствующие цены этих товаров, получаем приобретаемое сверх минимума аi количество i-го товара. Частный случай модели Стоуна. 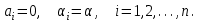 (50) В этом случае из (26.28) получаем:  (51) Уравнение Слуцкого. Функции спроса (45). При неизменной величине функции полезности в точке локального рыночного равновесия u(x1*,x2*,…,xn*) = const (52) (на гиперповерхности уровня этой функции) приращение функции xi* , обусловленное изменением только величины цены pj , равно: 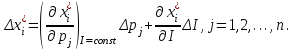   Поделив обе части на и переходя к пределу при получаем: 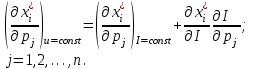 (53) П  оскольку I= p1x1* + p2x2* + …+ pnxn* , то при изменении цены pj на величину приращение дохода I составит: оскольку I= p1x1* + p2x2* + …+ pnxn* , то при изменении цены pj на величину приращение дохода I составит: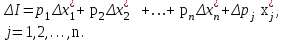 (54) (54) Как следствие из (52) получаем, что 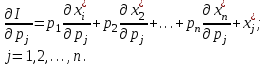 (55) (55)Так как дифференциал от функции (52) равен нулю, имеем соотношение: 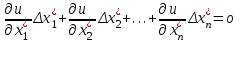 (56) В точке локального рыночного равновесия, в силу (26.23), имеем соотношения пропорциональности первых производных функции полезности и соответствующих цен:  После подстановки этих соотношений в (44) и сокращения обеих частей на сомножитель , получаем:  (57) После деления соотношения (57) на p j и предельного перехода при p j 0 получаем, что 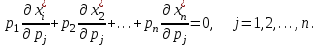 Подстановка этих уравнений в (55) приводит к формулам: 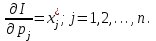 т.е. в точке рыночного равновесия относительное изменение дохода, вызванное изменением цены на товар, равно количеству этого товара. Подставляя это формулы в формулы (26.32), окончательно получаем: 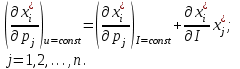 (58) Поскольку первое слагаемое в правой части представляет собой действие эффекта изменения цены при неизменном доходе на компнсационную добавку величины продукта, то это слагаемое называется компенсационным. Само же уравнение Слуцкого получается при переносе второго слагаемого в другую часть и используется в следующей форме: 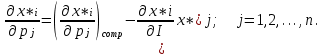 (59) Экономический смысл уравнения Слуцкого (59). Левая часть уравнения (59) представляет собой “отклик” точки спроса при неизменном доходе на изменение цены j-го товара. Второе слагаемое в правой части описывает действие эффекта дохода: это произведение, в котором одним из сомножителей является “отклик” точки спроса на изменение дохода I, а другим – величина спроса на j-й товар. Первое слагаемое в правой части (59) интерпретируется следующим образом: при изменении цены j-го товара на p j при неизменных остальных ценах и доходе изменяются точка спроса и максимальная полезность; изменим доход так, чтобы значение максимальной полезности осталось неизменным – это и является компенсацией. К уравнению Слуцкого присоединяется ряд соотношений, которые получаются в процессе его вывода. Перечислим их, поскольку они носят четкий экономический характер. Часть их мы приводим ниже без вывода. Итак, в точке локального рыночного равновесия (45) справедливы следующие соотношения. Уравнение (57): p  1 x*1 + p 2 x*2 + … + p n x*n = 0 . Это уравнение связывает прежние цены с приращениями товаров, что придает сложный характер изменению спроса: спрос на одни блага растет, на другие он падает. Из уравнения (54) с учетом (57) получаем: 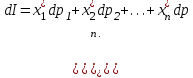 (60) Это соотношение означает, что при увеличении цен компенсация дохода должна быть положительной, а при уменьшении цен - отрицательной, что достаточно очевидно. 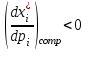 . . (61) 3 Это означает, что при повышении цены спрос на товар падает даже при компенсации дохода. 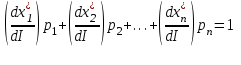 4. (62) Это уравнение показывает, что часть слагаемых суммируется со знаком плюс, а часть-со знаком минус. Товар называется “ценным”, если при повышении дохода спрос на него растет, в противном случае товар является малоценным. Из (62) следует, что не все слагаемые отрицательны, т.е. существуют ценные товары. Например, высококачественные продукты и предметы роскоши являются ценными, маргарин-малоценным. При повышении дохода употребление высококачественного масла возрастает. 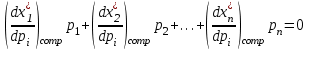 5. (63) |
