Экономико-матмодели. Выделить и формально описать наиболее существенные связи экономических объектов
 Скачать 461.57 Kb. Скачать 461.57 Kb.
|
|
ЭЛЕМЕНТЫ УПРАВЛЕНИЯ РИСКАМИ В ЭКОНОМИКЕ Оптимизация портфелей банка Математическая постановка задачи оптимального планирования системы портфелей банка заключается в следующем. Требуется найти неизвестные векторы активов и пассивов банка – соответственно A = ( A1 , A2 , … , An ) и L = ( L1 ,L2, … , Ln ),(64) максимизирующее линейную форму прибыли системы портфелей: 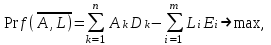 (65) В рамках сформулированной задачи можно выделить управление активами банка, суть которого выражается в следующем. Нужно максимизировать целевую функцию MA = p fM ( rM , rA , rB , … , W ) max дохода , (66) При формировании портфеля активов встает еще одна задача, имеющая противоположную цель, - минимизация риска, т.е. на допустимом множестве решений имеется такое, чтобы помимо цели (66) целевая функция удовлетворяла бы также условию: 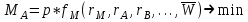 риска. (67) Портфельный анализ Метод, применяемый для выбора наиболее желательного портфеля, использует кривые безразличия. Иными словами, для инвестора существует функция полезности, зависящая от двух аргументов – ожидаемой доходности портфеля rp и стандартного отклонения (меры риска) р: (68)  Все портфели, лежащие на одной линии безразличия или линии уровня функции (68) 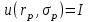 (69) я 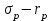 вляются равноценными для инвестора. Линии безразличия отражают отношение инвестора к рику и доходности портфеля и представляют собой кривые в координатах (рис. 4). Инвестор считает любой портфель, лежащий на линии безразличия выше и левее, более привлекательным, чем портфели, лежащие на линии безразличия, которая ниже и правее. вляются равноценными для инвестора. Линии безразличия отражают отношение инвестора к рику и доходности портфеля и представляют собой кривые в координатах (рис. 4). Инвестор считает любой портфель, лежащий на линии безразличия выше и левее, более привлекательным, чем портфели, лежащие на линии безразличия, которая ниже и правее. Ожидаемая доходность портфеля, состоящего из n ценных бумаг, равна  ((70) где xi – доля начальной стоимости портфеля, инвестированная в i-й вид ценных бумаг, ri – ожидаемая доходность i-го вида ценных бумаг, n – количество видов ценных бумаг в портфеле. Рис. 4                                                             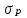   Стандартное отклонение портфеля rp вычисляется следующим образом. Дисперсия доходности портфеля – это дисперсия суммы случайных величин; как известно из теории математической статистики, она равна ковариации : 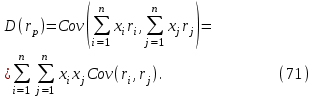  Здесь Cov(ri,rj) – ковариация ожидаемых доходностей ценных бумаг i и j, вычисляемая по формуле Где 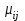 - коэффициент корреляции между доходностями - коэффициент корреляции между доходностями  -й и -й и 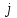 -й ценных бумаг, D и -й ценных бумаг, D и 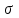 - соответственно дисперсия и стандартное (среднее квадратическое отклонение) доходностей ценных бумаг. Как известно, - соответственно дисперсия и стандартное (среднее квадратическое отклонение) доходностей ценных бумаг. Как известно,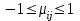 . .Формула для стандартного отклонения портфеля имеет вид: 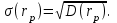 (73) (73)Пример 1. Найти ожидаемую доходность и стандартное отклонение доходности портфеля, состоящего из 30% акций компании А и 70% компании В, если их доходности некоррелированы и равны соответственно 20% и 10%, а стандартные отклонения – 10% и 5%. Решение. По формуле (70) получаем: 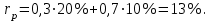 Поскольку доходности бумаг некоррелированы , то Поскольку доходности бумаг некоррелированы , то 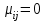 при при  и тогда и тогда  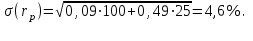  Приведённый пример показывает, что портфель ценных бумаг обладает меньшим риском, чем некоторые отдельные составляющие его бумаги. Это свойство портфеля называется диверсификацией: увеличение количества видов ценных бумаг при одновременном сокращении их долей в общей ожидаемой доходности уменьшает риск портфеля. Пример 2. Найти ожидаемую доходность и её стандартное отклонение для портфеля, состоящего из 10 видов ценных бумаг с некоррелированными доходностями. Доли ценных бумаг 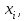 их доходности их доходности 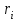 и стандартные отклонения и стандартные отклонения 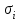 приведены в таблице. приведены в таблице.Таблица 1.
Решение. rp = 0,1 · 15 + 0,1 · 15 + 0,1 · 18 + 0,1 · 12 + 0,1 · 25 + 0,1 · 20 + 0,2 · 10 + 0,1 · 28 + + 0,005 · 35 + 0,005 · 40 = 19,05 %. Так как случайные величины доходностей бумаг являются независимыми, то дисперсия доходности портфеля равна D ( rp ) = 0,01 · 64 + 0,01 · 64 + 0,01 · 100 + 0,01 · 49 + 0,01 · 144 + 0,01 · 100 + + 0,04 · 25 0,01 · 225 + 0,0025 · 400 + 0,0025 · 625 = 11,02. 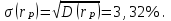 Тогда На рис. 5 показано достижимое множество, представляющее собой все портфели, которые можно сформировать из n видов ценных бумаг. Рис. 5 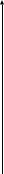  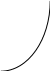 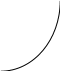   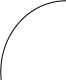              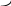 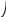     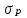   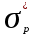  Рис. 6       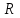                  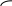   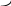  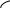  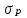  Методика VAR Классический способ измерения величины риска как стандартного отклонения ожидаемой доходности инвестиционного портфеля ( от рыночной стоимости ) имеет три существенных недостатка. 1. Завышение оценок риска, поскольку на величину дисперсии (28.8) одинаково влияют как отклонения от средних доходностей ценных бумаг со знаком минус, характеризующие потери (отрицательное изменение стоимости), так и со знаком плюс, характеризующие прибыль (положительное изменение стоимости). Иными словами, формально наименьшая степень риска соответствует ситуации, когда любые отклонения от средних доходностей ценных бумаг, в том числе и в положительную сторону, будут по возможности минимальными. 2. В случае распределения вероятностей, существенно отличного от нормального, особенно для асимметричных распределений, происходит искажение (как увеличение, так и уменьшение) величины риска. 3. Оценка риска в виде стандартного отклонения затрудняет процесс управления риском, так как не показывает величину возможных денежных потерь. Параметр VAR характеризует величину потерь, при которой потери в стоимости инвестиционного портфеля за определенный период времени То не превысят этой величины (потери понимаются как отрицательное изменение стоимости). Заметим, что в Базельской методике оценивается вероятность отрицательного изменения стоимости (потерь) выше определенного уровня потерь; этот уровень потерь и представляет собой определяемый параметр VAR. Под термином VAR понимают как методику (совокупность отдельных методов) оценки риска, так и количественную оценку рыночного риска в виде единственног параметра. VAR – это выраженная в данных денежных единицах (базовой валюте) оценка максимальных, ожидаемых в течение данного периода времени с данной вероятностью потерь данного портфеля под воздействием рыночных факторов риска. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||
