теорема пифагора. Виды доказательства теоремы Пифагора
 Скачать 105.5 Kb.
|
∆AСD по I признаку подобия треугольников.Средняя общеобразовательная школа №22. Города Курска Курской области РЕФЕРАТ На тему: «Виды доказательства теоремы Пифагора» Выполнил: Литвинова Анна 8 «б» Курск, 2023 СОДЕРЖАНИЕ ВВЕДЕНИЕ 2 2. ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ ПИФАГОРА 5 2.1 Доказательство способом достроения квадрата 6 2.2 Доказательство, используя пропорциональные отрезки 7 2.3 Доказательство, используя подобие треугольников 7 2.4 Доказательство, основанное на использовании понятия равновеликости фигур 7 2.5 Аддитивные доказательства 8 ЗАКЛЮЧЕНИЕ 9 ВВЕДЕНИЕТрудно найти человека, у которого имя Пифагора не ассоциировалось бы с теоремой Пифагора. Пожалуй, даже те, кто в своей жизни навсегда распрощался с математикой, сохраняют воспоминания о «пифагоровых штанах» — квадрате на гипотенузе, равновеликом двум квадратам на катетах. Причина такой популярности теоремы Пифагора триедина: это простота — красота — значимость. В самом деле, теорема Пифагора проста, но не очевидна. Это сочетание двух противоречивых начал и придает ей особую притягательную силу, делает ее красивой. Но, кроме того, теорема Пифагора имеет огромное значение: она применяется в геометрии буквально на каждом шагу, и тот факт, что существует около 500 различных доказательств этой теоремы (геометрических, алгебраических, механических и т.д.), свидетельствует о гигантском числе ее конкретных реализаций. Эта теорема формулировалась по-разному и появлялась в разных местах земного шара и в разное время. А объяснить и доказать эту теорему смог только Пифагор. Узнав о том, что существует очень много доказательств теоремы Пифагора, я заинтересовалась этим и решила изучить теорему Пифагора. Цель исследования - показать универсальность теоремы, рассмотрев различные способы доказательства. Задачи: - изучить биографию Пифагора; - рассмотреть доказательства теоремы Пифагора. Работа состоит из введения, 2 глав , заключения и списка литературы. 1. БИОГРАФИЯ ПИФАГОРА Пифагор родился в 580 г. до н.э. в Древней Греции на острове Самос, который находится в Эгейском море у берегов Малой Азии, поэтому его называют Пифагором Самосским. Родился Пифагор в семье резчика по камню. Сведения о его матери не сохранились. Родившийся мальчик был сказочно красив, а вскоре проявил незаурядные способности. Увлекался музыкой и поэзией, был победителем олимпийских игр по кулачному бою. Неугомонному воображению Пифагора стало тесно на маленьком острове. Мудрый Ферекид – один из учителей Пифагора однажды сказал: «Ты вырос из Самоса, отправляйся путешествовать – только так ты утолишь жажду познаний. Помни: путешествие и память – суть да средства, возвышающие человека и открывающие ему врата мудрости». Пифагор перебрался в город Милеет и стал учеником Фалеса, которому в то время шёл восьмой десяток. Под его руководством Пифагор изучает математику и небесную механику. Мудрый учёный посоветовал юноше отправиться в Египет, где сам, когда-то изучал науки. Перед Пифагором открылась неизвестная страна. Знания были сосредоточены в храмах, доступ в которые был ограничен. Пифагору потребовались годы, чтобы глубоко изучить египетскую культуру прежде, чем, ему было разрешено познакомиться с многовековыми достижениями египетской науки. Когда Пифагор постиг науку египетских жрецов, то засобирался домой, чтобы там создать свою школу. Жрецы, не желавшие распространения своих знаний за пределы храмов, не хотели его отпускать. С большим трудом ему удалось преодолеть эту преграду. Однако по дороге домой, Пифагор попал в плен и оказался в Вавилоне. Это несчастье сыграло счастливую роль в судьбе Пифагора: вавилонская математика была передовой наукой того времени, и у халдейских мудрецов было чему поучиться. Вавилоняне ценили умных людей, поэтому он нашёл своё место среди вавилонских мудрецов. Наука Вавилона была более развитой, нежели египетская. Наиболее поразительными были успехи алгебры. Вавилоняне изобрели и применяли при счёте позиционную систему счисления, умели решать линейные, квадратные и некоторые виды кубических уравнений. Пифагор прожил в Вавилоне около десяти лет и в сорокалетнем возрасте вернулся на родину. Но на острове Самос он оставался недолго. В знак протеста против тирана Поликрата, который тогда правил островом, поселился в одной из греческих колоний Южной Италии в городе Кротоне. Там Пифагор организовал тайный союз молодёжи из представителей аристократии. В этот союз принимались с большими церемониями после долгих испытаний. Каждый вступающий отрекался от своего имущества и давал клятву хранить в тайне учения основателя. Пифагорейцы, как их позднее стали называть, занимались математикой, философией, естественными науками. В конце V в. до н.э. после неудачного выступления на политической арене пифагорейцы были изгнаны из городов Южной Италии, и их союз распался. Пифагорейцы бежали из Кротона в другие города, что во многом способствовало распространению учения Пифагора по всей Греции и даже за её пределы. Сам Пифагор удалился в город Метапонт, расположенный неподалеку от Кротон, где провел остаток своей жизни. Смерть Пифагора также окружена красивыми легендами: - по одной из них, в Кротоне, где Пифагор собирался со своими учениками, был подожжен. Умер Пифагор около 500 г. до н.э.; - по другой – он был убит злоумышленниками в окрестностях города; - по третьей – он скончался в храме после сорокадневного голодания[4]. 2. ДОКАЗАТЕЛЬСТВА ТЕОРЕМЫ ПИФАГОРАВ научной литературе зафиксировано не менее 400 доказательств теоремы Пифагора, что объясняется как фундаментальным значением для геометрии, так и элементарностью результата. Основные направления доказательств: алгебраическое использование соотношенийэлементов треугольника, метод площадей, существуют также различные экзотические доказательства. Теорема. Квадрат гипотенузы равен сумме квадратов катетов 2.1 Доказательство способом достроения квадратаД 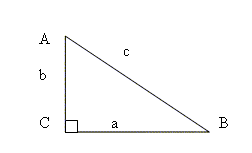 ано: прямоугольный треугольник АВС, ВС=a, АС=bи АВ=сДоказать: с2= а2+ в2 Доказательство: Достроим этот треугольник до квадрата со сторонойa+bследующим образом. П 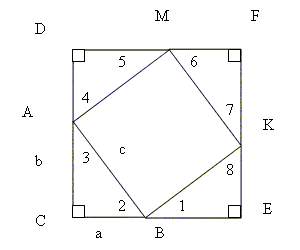 родолжим стороны АС и ВС за точки А и В соответственно, от точки А на продолжении стороны АС отложим отрезок, равный а, а от точки В на продолжении стороны ВС отрезок, равный b. Обозначим полученные точкиD и E соответственно. Через Е проведём прямую, параллельную АС, а через точку D прямую, параллельную СВ. Обозначим точку пересечения проведённых прямых за F. От точки F на отрезке DF отложим отрезок, равный а, а на отрезке FE, отрезок, равный b. Обозначим получившиеся точки М и К соответственно. Проведём отрезки АМ, МК и ВК.Полученный квадрат состоит из 4 равных прямоугольных треугольников (по 2 катетам) и одного четырёхугольника – квадрата Площадь большого квадрата равна (a+b)2, а с другой стороны с2+2(ab). Т.е. получили равенство: (a+b)2= с2+2(ab). После раскрытия скобок и упрощения получим с2= а2+ в2,что и требовалось доказать 2.2 Доказательство, используя пропорциональные отрезки Дано: ∆АВС < С=900 Доказать: АС²+ВС2=АВ² Пусть АВС данный прямоугольный треугольник с прямым углом С. Проведем высоту CD из вершины прямого угла С. По определению косинуса угла. cos A = AD/AC=AC/AB => ABхAD=AC² (1) сos B = BD/BC=BC/AB => BDхAB=BC² (2) Складывая почленно равенства (1) и (2) и учитывая, что AD +DB = AB, получимAC² +BC² =AB(AD+DB)=AB², что и требовалось доказать[1] 2.3 Доказательство, используя подобие треугольниковД ано: ∆АВС < С=90Доказать: а² + в² =с² Доказательство: Пусть S ∆AВС=S, S ∆ВСD=Sа, S ∆AСD=Sв. ∆AВС |
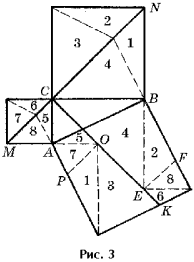оказательство Энштейна (рис. 3) основано на разложении квадрата,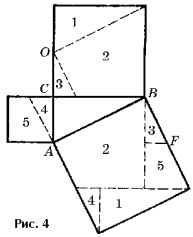 
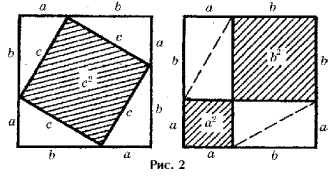
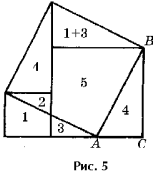а основе доказательства ан-Найризия выполнено и другое разложение квадратов на попарно равные фигуры (рис. 5, здесь ABC – прямоугольный треугольник с прямым углом C).
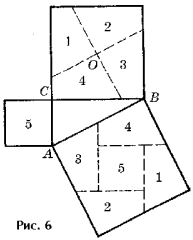то разложение квадратов интересно тем, что его попарно равные четырехугольники могут быть отображены друг на друга параллельным переносом. Может быть предложено много и других доказательств теоремы Пифагора с помощью разложения квадратов на фигуры.