хз. Экзамен Физика. Виды гармонических осцилляторов и их краткая характеристика
 Скачать 0.99 Mb.
|
|
Виды гармонических осцилляторов и их краткая характеристика. Тела, которые при движении совершают гармонические колебания, называют гармоническими осциляторами. Рассмотрим ряд примеров гармонических осциляторов. Пружинный маятник – это тело массой m, способное совершать колебания под действием силы упругости невесомой пружины. При смещении тела на расстояние х от положения равновесия О на него действует сила упругости пружины, направленная к положению равновесия:  , где k - коэффициент упругости (жесткости) пружины.Таким образом, колебания пружинного маятника - гармонические с циклической частотой  и периодом .Физический маятник - это твердое тело, совершающее колебания под действием силы тяжести вокруг подвижной горизонтальной оси, не совпадающей с его центром тяжести С Е  сли маятник отклонить от положения равновесия на малый угол и отпустить, он будет совершать колебания, следуя основному уравнению динамики вращательного движения твердого тела , где J - момент инерции маятника относительно оси, М ‑ момент силы, возвращающей физический маятник в положение равновесия. Таким образом, при малых отклонениях от положения равновесия физический маятник совершает гармонические колебания с циклической частотой  и периодом .Математический маятник - это материальная точка с массой m (тяжелый шарик малых размеров), подвешенная на невесомой (по сравнению с m шарика), упругой, нерастяжимой нити длинною l. Если вывести шарик из положения равновесия, отклонив его от вертикали на небольшой угол , а затем отпустить, он будет совершать колебания. Если рассматривать данную систему как физический маятник с моментом инерции материальной точки J = ml2, то из формул для физического маятника получим выражения для циклической частоты и периода колебаний математического маятника  ,  .Виды и признаки колебательного движения. В физике особенно выделяют колебания двух видов – механические и электромагнитные и их электромеханические комбинации, поскольку они чрезвычайно актуальны для жизнедеятельности человека. Так, механические колебания плотности воздуха воспринимаются нами как звук, а быстрые электромагнитные колебания – как свет. Для колебаний характерно превращение одного вида энергии в другой: кинетической - в потенциальную, магнитной - в электрическую и т.д. Свободными или собственными называют такие колебания, которые происходят в системе, предоставленной самой себе после того, как ей была сообщена энергия, либо система была выведена из положения равновесия (например, шарик, подвешенный на нити). Вынужденными называют такие колебания, в процессе которых колеблющаяся система подвергается воздействию внешней периодической силы (например, колебания моста при прохождении по нему поезда или раскачивание человеком качелей). Автоколебания, как вынужденные колебания, сопровождаются воздействием на колеблющуюся систему внешних сил, однако момент времени, когда осуществляются эти воздействия, задаются самой колеблющейся системой – система сама управляет внешним воздействием. Признаки колебаний: повторяемость (периодичность) – движение по одной и той же траектории туда и обратно; ограниченность пределами крайних положений; действие силы, описываемой функцией F = –k x. Вынужденные электрические колебания. Резонанс. Свободные электромагнитные колебания происходят с частотой, определяемой параметрами контура 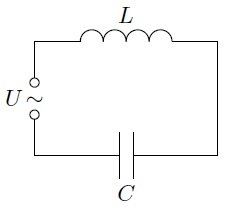 ,  и  , и в реальном колебательном контуре со временем затухают из-за потерь энергии. Чтобы получить незатухающие колебания, потери энергии необходимо компенсировать. Таким образом, для получения незатухающих электромагнитных колебаний необходимо ввести в контур э.д.с., периодически меняющуюся с течением времени по гармоническому закону:  Вынужденными называются электромагнитные колебания, которые происходят под действием периодически изменяющейся эдс Электрический резонанс - явление резкого возрастания амплитуды вынужденных колебаний, когда частота вынуждающей эдс  приближается к собственной частоте колебательного контура  .Чем больше сопротивление контура R, тем более полого располагается резонансная кривая Добротность колебательного контура. Критическое сопротивление. Добро́тность — параметр колебательной системы, определяющий ширину резонанса и характеризующий, во сколько раз запасы энергии в системе больше, чем потери энергии за время изменения фазы на 1 радиан. Обозначается символом {\displaystyle Q}  Добротность обратно пропорциональна скорости затухания собственных колебаний в системе. То есть, чем выше добротность колебательной системы, тем меньше потери энергии за каждый период и тем медленнее затухают колебания. 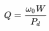 ,где  Критическое сопротивление контура – это такое сопротивление, при котором в контуре начинается апериодический разряд. В этом случае колебания в контуре отсутствуют, заряд на обкладках конденсатора убывает монотонно до нуля  Единицы измерения магнитных величин: Тесла, Ампер/метр.  Закон Ампера. Физический смысл магнитной индукции. Зако́н Ампе́ра — Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Сила оказывается линейно зависимой как от тока, так и от магнитной индукции Физически это явление объясняется следующим образом. Металл имеет кристаллическую структуру (катушка состоит из металла). В кристаллической решетке металла расположены электрические заряды — электроны. Если на металл не оказывать ни какое магнитное воздействие, то заряды (электроны) находятся в покое и никуда не движутся. В результате чего в металле возникает электрический ток. Сила этого тока зависит от физических свойств магнита и катушки и скорости перемещения одного относительно другого. При помещении металлической катушки в магнитное поле заряженные частицы металлический решетки (в кашутке) поворачиваются на определенный угол и размещаются вдоль силовых линий магнитного поля. Магнитные поля, ориентированные в одном направлении не нейтрализуют друг друга, а складываются, формируя единое поле. Закон Био-Саварра-Лапласса. Сила Лоренца. 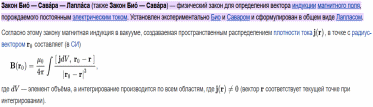 Силу, действующую со стороны магнитного поля на движущиеся в нем заряды, называют силой Лоренца. Сила Лоренца определяется соотношением: Fл = q·V·B·sina где q - величина движущегося заряда; V - модуль его скорости; B - модуль вектора индукции магнитного поля; a - угол между вектором скорости заряда и вектором магнитной индукции. Закон взаимосвязи массы и энергии. Закон сохранения энергии. Кинетическая энергия релятивистской частицы. Поскольку кинетическая энергия равна произведению массы на квадрат скорости, то, выходит, что при возрастании скорости энергия тела растет не только за счет увеличения скорости, но и за счет увеличения массы. А это означает взаимосвязь массы и энергии. И, кроме того, это значит, что даже при малых скоростях масса тела представляет некоторую энергию. При сообщении телу энергии его масса растет прямо пропорционально полученной энергии. Данное соотношение можно распространить не только на изменение массы, получаемое телом при изменении его энергии, но и на всю массу тела, в том числе на массу покоя. В результате получаем знаменитую формулу Эйнштейна, связывающую массу и энергию: E=mc2 То есть, согласно закону взаимосвязи массы и энергии, любая масса обладает энергией просто уже в результате своего существования. Закон сохранения энергии - энергия тел никуда не исчезает, а лишь переходит из кинетической в потенциальную и наоборот – из потенциальной в кинетическую. Релятивистская энергия составляет сумму собственной энергии частицы и релятивистской кинетической энергии 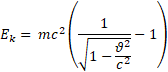  Закон сохранения заряда. Зако́н сохране́ния электри́ческого заря́да гласит, что алгебраическая сумма зарядов электрически замкнутой системы сохраняется.  Закон сохранения заряда в интегральной форме Вспомним, что плотность потока электрического заряда есть просто плотность тока. Тот факт, что изменение заряда в объёме равно полному току через поверхность, можно записать в математической форме: 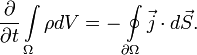 Закон сохранения заряда в дифференциальной форме Переходя к бесконечно малому объёму и используя по мере необходимости теорему Стокса можно переписать закон сохранения заряда в локальной дифференциальной форме (уравнение непрерывности)  Закон Фарадея. Правило Ленца. Зако́н электромагни́тной инду́кции Фараде́я является основным законом электродинамики, Закон гласит: Для любого контура индуцированная электродвижущая сила (ЭДС) равна скорости изменения магнитного потока, проходящего через этот контур, взятой со знаком минус.  Правило Ленца определяет направление индукционного тока и гласит: Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток. Импеданс. Активное и реактивное сопротивления. Электрический импеданс (комплексное сопротивление, полное сопротивление) — это комплексное сопротивление аналог понятия сопротивления для постоянного тока в приложении к синусоидальному току. Такое понятие позволяет применить закон Ома для участка цепи в случае синусоидальных токов. Если двухполючник имеет проявление индуктивной составляющей на данной частоте, то синусоидальный ток будет отставать от напряжения на зажимах двухполюсника, а если имеет проявление ёмкостной составляющей, то напряжение будет отставать от тока. Если двухполюсник — активный, то задержки между током и напряжением не будет. Если реактивную составляющую импеданса X отложить по оcи Y c соответствующим знаком, а активную R по оси X, то получится графическая интерпретация импеданса как комплексного числа  Где R – величина активного сопротивления, а X – величина реактивного сопротивления. Активное сопротивление — физическая величина, характеризующая сопротивление электрической цепи (или её участка) электрическому току, обусловленное необратимыми превращениями электрической энергии в другие формы (преимущественно в тепловую). Выражается в омах. Однако многие потребители обладают индуктивными и емкостными свойствами при прохождении через них переменного тока. К таким потребителям относятся трансформаторы, дроссели, электромагниты, конденсаторы, различного рода провода и многие другие. При прохождении через них переменного тока необходимо учитывать не только активное, но и реактивное сопротивление, обусловленное наличием, в потребителе индуктивных и емкостных свойств его. Кинематическое описание движения материальной точки. Ускорение тел. Полное, нормальное и тангенциальное ускорения. Кинематика изучает движение без выявления причин, вызывающих это движение. Кинематика является разделом механики. Главной задачей кинематики является математическое определение положения и характеристик движения точек или тел во времени. Основные кинематические величины: - Перемещение(  ) –вектор, соединяющий начальную и конечную точки. r – радиус-вектор, определяет положение МТ в пространстве. - Скорость – отношение пути ко времени.  - Путь – множество точек через которое прошло тело.    - Ускорение – скорость изменения скорости, то есть первая производная от скорости.  Полное ускорение при равнопеременном криволинейном движении тела равно:  Нормальное ускорение - это изменение скорости по направлению за единицу времени:  Изменение величины скорости за единицу времени – это тангенциальное ускорение: +  Когерентные колебания. Биения. Когерентность (от латинского cohaerens — находящийся в связи), согласованное протекание во времени нескольких колебательных или волновых процессов, проявляющееся при их сложении. Колебания называются когерентными, если разность их фаз остаётся постоянной во времени и при сложении колебаний определяет амплитуду суммарного колебания. Два гармонических (синусоидальных) колебания одной частоты всегда когерентны. Периодические изменения амплитуды колебания, возникающие при сложении двух гармонических колебаний с близкими частотами, называются биениями. Строго говоря, это уже не гармонические колебания. Колебательный контур. Основное уравнение колебаний в контуре. Колебательный контур — электрическая цепь, содержащая катушку индуктивности, конденсатор и источник электрической энергии. 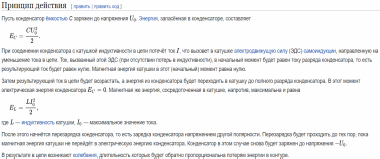 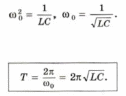 Коэффициент затухания. Логарифмический декремент затухания. Следовательно, коэффициент затухания β есть физическая величина, обратная времени, в течение которого амплитуда уменьшается в е раз. Следовательно, логарифмический декремент затухания χ есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз. 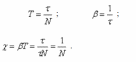 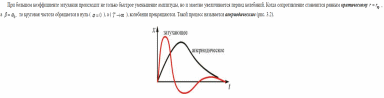 Магнитная проницаемость. Магнитная постоянная. Магни́тная проница́емость — безразмерная физическая величина, характеризующая изменение магнитной индукции В среды под воздействием магнитного поля и напряженностью Н. Магнитная проницаемость различна для разных сред и зависит от ее свойств, поэтому принято говорить о магнитной проницаемости конкретной среды (имея вввиду ее состав, состояние, температуру и т. д.). В случае однородной изотропной среды магнитная проницаемость μ: μ = В/(μoН), где μo — магнитная постоянная. μo=1.3*10-6Гн/м. Большинство веществ по значению магнитной проницаемости делятся на три класа: диамагнетики (μ < 1), парамагнетики (μ > 1) ферромагнетики (обладающие более выраженными магнитными свойствами, например железо). Магнитная проницаемость сверхпроводников равна нулю. Абсолютная магнитная проницаемость воздуха приблизительно равна магнитной проницаемости вакуума и в технических расчетах принимается равной 4π · 10-7 Гн/м Магнитное поле. Причины магнитного взаимодействия. Магни́тное по́ле — поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения[1]; магнитная составляющая электромагнитного поля[2]. Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, что обычно проявляется в существенно меньшей степени) (постоянные магниты). Кроме этого, оно возникает в результате изменения во времени электрического поля. Основной количественной характеристикой магнитного поля является вектор магнитной индукции Магнитное поле создаётся (порождается) током заряженных частиц, или изменяющимся во времени электрическим полем, или собственными магнитными моментами частиц. Одно из наиболее часто встречающихся в обычной жизни проявлений магнитного поля — взаимодействие двух магнитов: одинаковые полюса отталкиваются, противоположные притягиваются. Магнитный гистерезис и коэрцитивная сила. Магнитный гистерезис — явление зависимости вектора намагниченности M и вектора магнитной индукции B в веществе не только от напряжённости H приложенного внешнего поля, но и от предыстории данного образца. Магнитный гистерезис обычно проявляется в ферромагнетиках — Fe, Co, Ni и сплавах на их основе. Магнитным гистерезисом объясняется существование постоянных магнитов. Зависимости M(H) и B(H) имеют вид петли, размах которой по вертикали зависит от ширины диапазона изменения напряжённости поля H. 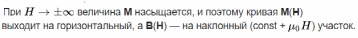 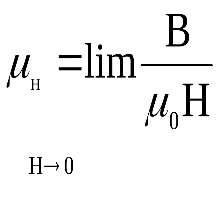 где μн-начальная магнитная проницаемость.Коэрцити́вная си́ла (от лат. coercitio «удерживание») — это значение напряжённости внешнего магнитного поля, необходимое для полного размагничивания ферримагнитного вещества. Единица измерения коэрцитивной силы совпадает с единицей напряжённости магнитного поля и в (СИ) — ампер/метр Обычно обозначается Hс Макротоки и микротоки. Намагниченность. При изучении магнитного поля в веществе различают два типа токов – макротоки и микротоки. Макротоками называются токи проводимости и конвекционные токи, связанные с движением заряженных макроскопических тел. Микротоками (молекулярными токами) называют токи, обусловленные движением электронов в атомах, молекулах и ионах. Магнитное поле в веществе является суперпозицией двух полей: внешнего магнитного поля, создаваемого макротоками и внутреннего, или собственного, магнитного поля, создаваемого микротоками. Характеризует магнитное поле в веществе вектор  , равный геометрической сумме  и  магнитных полей:
Количественной характеристикой намагниченного состояния вещества служит векторная величина – намагниченность  , равная отношению магнитного момента малого объема вещества к величине этого объема:
где  – магнитный момент i-го атома из числа n атомов, в объеме ΔV.Масса. Сила. Масса [кг] – скалярная физическая величина, характеризующая количество вещества. Сила [н = 1 кг*м/с2 ] - векторная физическая величина, являющаяся мерой действия на данное тело других тел. Сила характеризуется: модулем, направлением, точкой приложения. Второй закон Ньютона: Ускорение тела прямо пропорционально равнодействующей сил, приложенных к телу, и обратно пропорционально его массе:   Международная система единиц. Основные единицы. Единицы измерения Международная система единиц (СИ) (фр. Le Système International d'Unités (SI)) — система единиц физических величин, современный вариант метрической системы. СИ определяет семь основных и производные единицы физических величин (далее - единицы), а также набор приставок. Установлены стандартные сокращённые обозначения для единиц и правила записи производных единиц. Основные единицы: килограмм, метр, секунда, ампер, кельвин, моль и кандела. 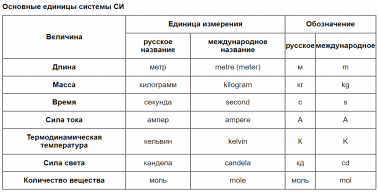 Момент импульса. Закон сохранения момента импульса. Моме́нт и́мпульса (момент импульса относительно точки, также: кинетический момент, угловой момент, орбитальный момент, момент количества движения) — физическая величина, характеризующая количество вращательного движения и зависящая от того, сколько массы вращается, как она распределена в пространстве и с какой угловой скоростью происходит вращение[1].  Зако́н сохране́ния моме́нта и́мпульса (закон сохранения углового момента) — один из фундаментальных законов сохранения. Математически выражается через векторную сумму всех моментов импульса относительно выбранной оси для замкнутой системы тел, которая остается постоянной, пока на систему не воздействуют моменты внешних сил. В соответствии с этим момент импульса замкнутой системы в любой системе координат не изменяется со временем.  где Li -{\displaystyle {\vec {L_{i}}}} момент импульса i{\displaystyle i} -той частицы, а суммирование производится по всем частицам замкнутой механической системы. Момент силы. Основной закон динамики вращательного движения.   Напряжённость магнитного поля. Магнитная восприимчивость среды.  Магни́тная восприи́мчивость — физическая величина, выражающая отношение между магнитным моментом единицы объёма (намагниченностью) вещества и напряжённостью магнитного поля в этом веществе.  Опыты Фарадея с катушкой и магнитом. Суть опытов, следствия из них. Если подносить постоянный магнит к катушке или наоборот, то в катушке возникнет электрический ток. 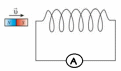 То же самое происходит с двумя близко расположенными катушками: если к одной из катушек подключить источник переменного тока, то в другой также возникнет переменный ток 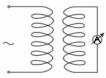 По определению Фарадея общим для этих опытов является следующее: если поток вектора индукции, пронизывающий замкнутый, проводящий контур, меняется, то в контуре возникает электрический ток. Это явление называют явлением электромагнитной индукции, а ток – индукционным. При этом явление совершенно не зависит от способа изменения потока вектора магнитной индукции. Итак, получается, что движущиеся заряды (ток) создают магнитное поле, а движущееся магнитное поле создает (вихревое) электрическое поле и собственно индукционный ток. Парамагнетик и диамагнетик: определение и основные свойства. Диамагнетиками называются вещества, магнитные моменты атомов которых в отсутствии внешнего поля равны нулю, т.к. магнитные моменты всех электронов атома взаимно скомпенсированы (например инертные газы, водород, азот, NaCl и др.). При внесении диамагнитного вещества в магнитное поле его атомы приобретают наведенные магнитные моменты. В пределах малого объема ΔV изотропного диамагнетика наведенные магнитные моменты  всех атомов одинаковы и направлены противоположно вектору .Вектор намагниченности диамагнетика равен:
где n0 – концентрация атомов,  – магнитная постоянная,  –магнитная восприимчивость среды.Для всех диамагнетиков  Таким образом, вектор магнитной индукции собственного магнитного поля, создаваемого диамагнетиком при его намагничивании во внешнем поле направлен в сторону, противоположную . (В отличие от диэлектрика в электрическом поле).У диамагнетиков  Парамагнетиками называются вещества, атомы которых имеют, в отсутствие внешнего магнитного поля, отличный от нуля магнитный момент  .Эти вещества намагничиваются в направлении вектора .К парамагнетикам относятся многие щелочные металлы, кислород  , оксид азота NO, хлорное железо  и др.В отсутствие внешнего магнитного поля намагниченность парамагнетика  , так как векторы  разных атомов ориентированы беспорядочно.При внесении парамагнетика во внешнее магнитное поле происходит преимущественная ориентация собственных магнитных моментов атомов  по направлению поля, так что парамагнетик намагничивается. Значения для парамагнетиков положительны (  ) и находятся в пределах  , то есть примерно как и у диамагнетиков.Параметры колебательного движения. Смещение, амплитуда и фаза колебания.  уравнение гармонического колебания колебательного движения Амплитуда –максимальное смещение от положения равновесия. [хm, м] Период –время одного полного колебания. Т =  =  [Т, с] Частота (линейная) –число полных колебаний за единицу времени. ν =  ν, [Гц (Герц)] Частота (круговаяили циклическая) –число колебаний, совершаемых материальной точкой за 2π/с. ω = 2πν =  Фаза колебаний– определяет состояние колебательной системы в любой момент времени.  , град или рад  Смещение –отклонение колеблющейся точки от положения равновесия в данный момент времени. [х, м] Первый закон Ньютона и понятие инерциальной системы отсчёта. Первый закон Ньютона постулирует существование инерциальных систем отсчёта. Поэтому он также известен как закон инерции. Инерция (она же инертность[3]) — свойство тела сохранять скорость своего движения неизменной по величине и направлению, когда не действуют никакие силы, а также свойство тела сопротивляться изменению его скорости. Чтобы изменить скорость движения тела, необходимо приложить некоторую силу, причём результат действия одной и той же силы на разные тела будет различным: тела обладают разной инерцией (инертностью), величина которой характеризуется их массой. Современная формулировка В современной физике первый закон Ньютона принято формулировать в следующем виде[4]:
Инерциа́льная систе́ма отсчёта (ИСО) — система отсчёта, в которой все свободные тела движутся прямолинейно и равномерно либо покоятся Полное колебание. Частота колебаний. Круговая частота колебаний. Потенциал. Связь потенциала с напряжённостью электрического поля. Потенциал это скалярная энергетическая характеристика электростатического поля. Потенциал, как и напряженность, подчиняется принципу суперпозиции. 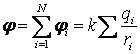 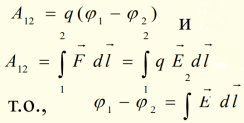 Потенциальная энергия. Консервативные и диссипативные силы и системы. Потенциа́льная эне́ргия — скалярная физическая величина, представляющая собой часть полной механической энергии системы (Е=Еп+Ек), находящейся в поле консервативных сил. Потенциальная энергия зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении   Кроме контактных взаимодействий, возникающих между соприкасающимися телами, наблюдаются взаимодействия между телами, удаленными друг от друга. Такие взаимодействия осуществляются посредством физических полей. Стационарное поле, в котором работа, совершаемая над частицей силами поля, зависит лишь от начального и конечного положений частицы и не зависит от пути, по которому она двигалась, называют потенциальным. Силы, действующие в потенциальных полях, называют консервативными. Работа консервативной силы на замкнутом пути равна нулю. Примеры консервативных сил – сила тяжести, сила упругости. Если же работа, совершаемая силой, зависит от траектории перемещения тела из одной точки в другую, то такая сила называется неконсервативной (или диссипативной). Типичные неконсервативные силы – силы трения. Поток вектора. Теорема Гаусса для электростатического поля в вакууме. Теорема Гаусса (закон Гаусса) — один из основных законов электродинамики, входит в систему уравнений Максвелла. Выражает связь (а именно равенство с точностью до постоянного коэффициента) между потоком напряжённости электрического поля сквозь замкнутую поверхность произвольной формы и алгебраической суммой зарядов, расположенных внутри объёма, ограниченного этой поверхностью. Применяется отдельно для вычисления электростатических полей. Теорема Гаусса для напряжённости электрического поля в вакууме Общая формулировка: Поток векторанапряжённости электрического поля через любую произвольно выбранную замкнутую поверхность пропорционален заключённому внутри этой поверхности электрическому заряду.  Причины электрического тока. Ток смещения и ток проводимости. Для возникновения электрического тока, требуется наличие свободных, не закрепленных заряженных частиц, которые в электростатическом поле неподвижных зарядов приходят в состояние упорядоченного движения вдоль силовых линий поля. Это движение и есть электрический ток. В природе можно выделить два вида токов: ток связанных зарядов и ток проводимости. Ток связанных зарядов (смещения) — это перемещение средних положений связанных электронов и ядер, составляющих молекулу, относительно центра молекулы. Ток проводимости — это направленное движение на большие расстояния свободных зарядов (например, ионов или свободных электронов). В случае, если этот ток идёт не в веществе, а в свободном пространстве, нередко вместо термина «ток проводимости» употребляют термин «ток переноса». Иначе говоря, ток переноса или ток конвекции обусловлен переносом электрических зарядов в свободном пространстве заряженными частицами или телами под действием электрического поля. В общем случае, токи проводимости и смещения в пространстве не разделены, они находятся в одном и том же объеме. Поэтому Максвелл ввёл понятие полного тока, равного сумме токов проводимости (а также конвекционных токов) и смещения. Плотность полного тока:  Работа и мощность тока. КПД источника тока. Работа. Мощность. Работа силы на участке траектории. Распространение волн в упругой среде. Фронт волны. Волновая поверхность. Связь потенциальной и кинетической энергий гармонических колебаний. Связь смещения, скорости и ускорения колебательного движения. Сложение взаимно перпендикулярных колебаний. Фигуры Лиссажу. Теорема Гаусса в интегральной форме и следствия из неё. Теорема Лармора. Ларморовская прецессия. Токи смещения и проводимости: определение и основные свойства. Третий закон Ньютона и закон сохранения импульса. Фазовая скорость. Дисперсия. Ферромагнетизм. Точка Кюри. Физические модели: материальная точка, система материальных точек, абсолютно твёрдое тело. Электрический (точечный) заряд. Закон сохранения заряда. Закон Кулона. Электроёмкость. Конденсаторы и их соединение. Эффект Пельтье. Эффект Зеебека. Явления самоиндукции и взаимоиндукции. |
,
,
,