статистика. вопросы экзамен статистика с ответами. Виды статистического наблюдения по охвату единиц совокупности
 Скачать 116.45 Kb. Скачать 116.45 Kb.
|
|
Виды статистического наблюдения по времени регистрации. Различают следующие виды наблюдения: В зависимости от охвата единиц совокупности: Сплошное наблюдение – регистрации подлежат все единицы изучаемой совокупности (перепись населения). Несплошное наблюдение охватывает определённую часть изучаемой совокупности и в свою очередь подразделяется на: Выборочное наблюдение, кода обследованию подвергается отобранная случайным образом часть единиц совокупности, а полученные результаты распространяются на всю совокупность. Наблюдение основного массива, когда обследованию подвергается основной массив – та часть единиц, которая вносит наибольший вклад в изучаемое явление. Монографическое наблюдение глубоко и всесторонне характеризует отдельные единицы совокупности. При этом не ставится цель охарактеризовать всю совокупность. По времени регистрации наблюдения: Непрерывное (текущее) наблюдение ведется систематически, постоянно, непрерывно, осуществляется путём непрерывной регистрации фактов по мере их возникновения. Прерывное наблюдение производится либо регулярно через равные промежутки времени, либо по мере надобности и подразделяется на: Периодическое, при котором регистрация проводится через определенные, обычно одинаковые промежутки времени. Единовременное, которое поводится один раз для решения какой-либо задачи или повторяется по мере надобности. Показатели ряда динамики. задачи: 1.Оценка скорости изменений явления во времени и выявление особенностей ряда. 2.Определяет осн. тенденцию или тенденции на определенных интервалах времени. 3.Выявляет факторы, обуславливающие изменение тенденции. 4.Делаются прогнозы развития явления на перспективу. Первая задача решается путем расчета показателей ряда динамики: ∆ — абсолютный прирост; К – темп роста (или коэффициент роста); Т – темп прироста; А – абсолютн. знач-е 1% прироста. Первые 3 показателя вычисляются двумя способами: цепным и базисным, последний – только цепным. При цепном способе расчета сравниваются 2 соседних уровня ряда. При базисном способе все показатели ряда оцениваются с первым, взятым за базу; чаще всего за базисный уровень принимается начальный уровень ряда. Кроме того, вычисляются средние показатели ряда: 1) средний уровень ряда; 2) средний абсолютный прирост; 3) средний темп роста; 4) средний темп прироста. Среднего А не существует. Графическое изображение вариационного ряда. Первым этапом изучения вариационного ряда является его графическое изображение. Дискретный вариационный ряд изображается в виде так называемого полигона, или многоугольника, распределения частот, являющегося разновидностью статистических ломаных. Для изображения интервального ряда применяются полигонраспределения частот и гистограмма частот. Строятся графики в прямоугольной системе координат. При построении полигона частот на оси абсцисс в одинаковом масштабе откладываются направо в порядке возрастания значения признака (для дискретного характера) или центральные значения интервалов (для интервальных рядов); по оси ординат наносится шкала для выражения величин частот. Из точек на оси абсцисс, соответствующих величине признака, восстанавливаются перпендикуляры высотой, соответствующей частоте; вершины перпендикуляров соединяются отрезками прямой. Крайние точки полученной ломаной соединяются с лежащими на оси абсцисс следующими (меньшими и большими) возможными, но фактически не наблюдающимися значениями признака, частота которых, очевидно, равна 0. Замкнутая с осью абсцисс ломаная линия представляет полигон распределения частот. Построим полигон частот по табл. 4.4. (рис.4.1) 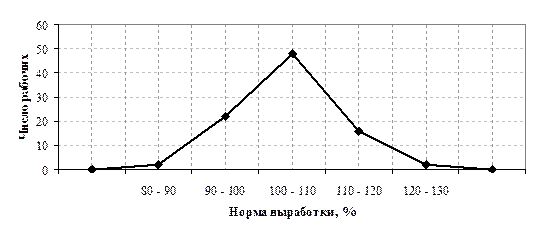 Рис. 4.1 – Полигон распределения рабочих по выполнению норм выработки Для построения гистограммы по оси абсцисс откладывают величины интервалов, а частоты изображаются прямоугольниками, построенными на интервалах с высотой в масштабе оси ординат (рис. 4.2). В случае неравенства интервалов гистограмма строится не по частотам или частостям, а по плотности распределения. 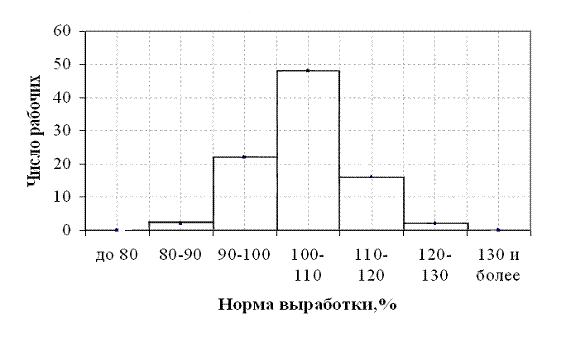 Рис. 4.2 – Гистограмма распределения рабочих по выполнению норм выработки В ряде случаев для изображения вариационных рядов используется кумулятивная кривая (кумулята (рис.4.3), она особенно удобна для сравнения вариационных рядов. Накопленные частоты наносятся на чертеж в виде ординат; соединяя вершины отдельных ординат прямыми, получают ломаную линию, которая, начиная с нуля, непрерывно поднимается над осью абсцисс, до тех пор пока не достигнет высоты, соответствующей общей сумме частот.  Рис. 4.3 – Кумулята распределения рабочих по выполнению норм выработки Если поменять местами оси координат в кумуляте, то получаем новый вид графического изображения - огиву. Стобиковые диаграммы, их значение, порядок построения. Наиболее распространенными диаграммами сравнения являются столбиковые диаграммы, принцип построения которых состоит в изображении статистических показателей в виде поставленных по вертикали прямоугольников – столбиков. Каждый столбик изображает величину отдельного уровня исследуемого статистического ряда. Таким образом, сравнение статистических показателей возможно потому, что все сравниваемые показатели выражены в одной единице измерения. По форме графического образа столбиковые диаграммы разделяются на плоскостные и объемные. При построении плоскостных столбиковых диаграмм необходимо начертить систему прямоугольных координат, в которой располагаются столбики. На горизонтальной оси располагаются основания (длина) столбиков, величина основания определяется произвольно, но устанавливается одинаковой для всех. Шкала, определяющая масштаб столбиков по высоте, расположена по вертикальной оси. Величина каждого столбика по вертикали соответствует размеру изображаемого на графике статистического показателя. Таким образом, у всех столбиков, составляющих диаграмму, переменной величиной является только одно измерение. При построении столбиковых диаграмм необходимо выполнять следующие требования: 1) шкала, по которой устанавливается высота столбика, должна начинаться с нуля; 2) шкала должна быть, как правило, непрерывной; 3) основания столбиков должны быть равны между собой; 4) наряду с разметкой шкалы соответствующими цифровыми надписями следует снабжать и сами столбцы. Покажем построение столбиковой диаграммы по данным Таблица 1 -Вклады граждан в учреждения Сбербанка за шесть месяцев 1999 г. (цифры условные) Месяц 1 2 3 4 5 6 Вклады, млн. руб. 560 640 1100 1630 1610 2500 9 В соответствии с изложенными выше правилами на горизонтальной оси размещаются основания шести столбиков на одинаковом расстоянии друг от друга, в данном случае 10 мм . Ширина столбиков принята 10 мм. Выбираем масштаб на оси ординат, например, 500 млн.руб. – 15 мм. Затем по оси y откладываются значения вкладов. Над полученными столбиками надписываются данные значения статистического показателя. Для выразительности столбики можно заштриховать или раскрасить. Наглядность данной диаграммы достигается сравнением величины столбиков. Размещение столбиков в поле графика может быть различным: на одинаковом расстоянии друг от друга ; вплотную друг к другу; в частном наложении друг на друга. Правила построения столбиковых диаграмм допускают одновременное расположение на одной горизонтальной оси изображений нескольких показателей. В этом случае столбики располагаются группами . При выполнении объемных столбиковых диаграмм сначала необходимо выбрать вид аксонометрической проекции (аксонометрии), на которую они проецируются. Здесь рекомендуется использовать косоугольные фронтальную изометрическую (кавальерную) (рис.11) и фронтальную диметрическую (кабинетную) (рис.12) проекции [2]. Разновидности столбиковых диаграмм составляют так называемые ленточные или полосовые диаграммы. Их отличие состоит в том, что масштабная шкала расположена по горизонтали сверху или снизу, и она определяет величину полос диаграммы. Область применения столбиковых и полосовых диаграмм одинакова, так как идентичны правила их построения. Относительные величины в статистике Относительная величина в статистике – это обобщающий показатель, который дает числовую меру соотношения двух сопоставляемых абсолютных величин. Так как многие абсолютные величины взаимосвязаны, то и относительные величины одного типа в ряде случаев могут определяться через относительные величины другого типа. Основное условие правильного расчета относительной величины – сопоставимость сравниваемых показателей и наличие реальных связей между изучаемыми явлениями. Таким образом, по способу получения относительные показатели – всегда величины производные, определяемые в форме коэффициентов, процентов, промилле, продецимилле и т.п. Однако нужно помнить, что этим безразмерным по форме показателям может быть, в сущности, приписана конкретная, и иногда довольно сложная, единица измерения. Так, например, относительные показатели естественного движения населения, такие как коэффициенты рождаемости или смертности, исчисляемые в промилле (‰), показывают число родившихся или умерших за год в расчете на 1 000 человек среднегодовой численности; относительная величина эффективности использования рабочего времени – это количество продукции в расчете на один отработанный человеко-час и т.д. Относительные величины образуют систему взаимосвязанных статистических показателей. По содержанию выражаемых количественных соотношений выделяют следующие типы относительных величин. 1. Относительная величина выполнения задания. Рассчитывается как отношение фактически достигнутого в данном периоде уровня к запланированному. Так, в 1988 г. было произведено стиральных машин 6103 тыс. шт. при плане (госзаказе) 6481 тыс. шт. Относительная величина выполнения плана составила Следовательно, плановое задание было недовыполнено на 5,8 %. На практике различают две разновидности относительных показателей выполнения плана. В первом случае сравниваются фактические и плановые уровни (таков пример, рассмотренный выше). Во втором случае в плановом задании устанавливается абсолютная величина прироста или снижения показателя и соответственно проверяется степень выполнения плана по этой величине. Так, если планировалось снизить себестоимость единицы продукции на 24,2 руб., а фактическое снижение составило 27,5 руб., то плановое задание по снижению себестоимости выполнено с ростом в 27,5 : 24,2 = 1,136 раза, т.е. план перевыполнен на 13,6 %. Показатель выполнения плана по уровню себестоимости в данном случае будет меньше единицы. Если фактическая себестоимость изделия равнялась 805,8 руб. при плановой 809,1 руб., то величина выполнения плана составила 805,8 : 809,1 = 0,996, или 99,6 %. Фактический уровень затратив одно изделие оказался на 0,4 % ниже планового. В аналитических расчетах при исследовании взаимосвязей чаще применяется оценка выполнения плана по уровню показателя. Оценка же выполнения плана по изменению уровня обычно приводится для целей иллюстрации, особенно если планируется снижение абсолютного значения затрат, расходов по видам и т.п. Относительные величины динамики, планового задания и выполнения плана связаны соотношением 2. Относительная величина динамики. Характеризует изменение уровня развития какого-либо явления во времени. Получается в результате деления уровня признака в определенный период или момент времени на уровень этого же показателя в предшествующий период или момент. Так, по данным топливно-энергетического баланса СССР, ресурсы 1980 г. оценивались в 2171,1 млн. т у.т.(условного топлива), а 1987 г. – в 2629,1 млн. т у.т. Относительная величина динамики составила Таким образом, объем топливно-энергетических ресурсов вырос за 7 лет в 1,211 раза (коэффициент роста, индекс роста, индекс). В процентном выражении это 121,1 % (темп роста). Иначе говоря, за 7 лет объем ресурсов увеличился на 21,1 % (темп прироста). В среднем каждый год объем ресурсов возрастал по сравнению с предыдущим годом в 3. Относительные величины структуры. Характеризуют доли, удельные веса составных элементов в общем итоге. Как правило, их получают в форме процентного содержания:  Для аналитических расчетов предпочтительнее использовать коэффициентное представление, без умножения на 100. Совокупность относительных величин структуры показывает строение изучаемого явления. 5. Относительные величины координации (ОВК). Характеризуют отношение частей данной совокупности к одной из них, принятой за базу сравнения. ОВК показывают, во сколько раз одна часть совокупности больше другой либо сколько единиц одной части приходится на 1, 10, 100, 1000, ... единиц другой части. Относительные величины координации могут рассчитываться и по абсолютным показателям, и по показателям структуры. Так, приняв за базу сравнения поставки топливных ресурсов на экспорт в 1987 г., увидим, что на каждую условную тонну экспортных поставок приходится в 2,342 раза больше ресурсов, потребляемых внутри страны для производства энергии, и в 2,363 раза больше ресурсов, предназначенных для производственно-технологических целей. Уровень остатков на конец года составляет 57,8 % по сравнению с годовыми поставками на экспорт (9,20 : 15,91 = 242 : 418,3 = 0,578). По относительным величинам координации можно восстановить исходные относительные показатели структуры, если вычислить отношение относительной величины координации данной части (ОВК) к сумме всех ОВК (включая и ту, которая принята за базу сравнения): Например, доля экспортных поставок составляет 1 : (2,342 + 2,364 + 1 + 0,578) = 0,1591, или 15,9 %. 6. Относительные величины сравнения (ОВС). Характеризуют сравнительные размеры одноименных абсолютных величин, относящихся к одному и тому же периоду либо моменту времени, но к различным объектам или территориям. Посредством этих показателей сопоставляются мощности различных видов оборудования, производительность труда отдельных рабочих, производство продукции данного вида разными предприятиями, районами, странами. Например, по производству нефти и газа в 1985 г. СССР превосходил США: по нефти – в 1,36 раза, по газу – в 1,24 раза. Уровень производства электроэнергии (млрд. кВт • ч) в СССР составлял от уровня США 1544:2650 = 0,583, или 58,3 %. При известных коэффициентах роста (индексах динамики) и начальном соотношении уровней можно найти условие равенства уровней в предстоящем периоде t: Отсюда ОВСa / б =Ya / Yб=(ia / iб)t, т.е. Найденное значение t показывает, через какой период времени уровень изучаемого явления на объекте А сравняется с уровнем того же явления на объекте Б. В частности, при среднегодовых темпах прироста производства электроэнергии в США 4,5 % и в СССР 6,9 % (по данным за 1961–1985 гг.) Сопоставляя показатели динамики разных явлений, получают еще один вид относительных величин сравнения – коэффициенты опережения (отставания) по темпам роста или прироста. Так, если производительность труда на предприятии возросла на 12%, а фонд оплаты труда увеличился на 7,5 %, то коэффициент опережения производительности труда по темпам роста составит 112 : 107,5 = 1,042; коэффициент опережения по темпам прироста равен 12 : 7,5 = 1,60. 7. Относительные величины интенсивности. Характеризуют степень распределения или развития данного явления в той или иной среде. Представляют собой отношение абсолютного уровня одного показателя, свойственного изучаемой среде, к другому абсолютному показателю, также присущему данной среде и, как правило, являющемуся для первого показателя факторным признаком. Так, при изучении демографических процессов рассчитываются показатели рождаемости, смертности, естественного прироста и т.д. как отношение числа родившихся (умерших) или величины прироста населения за год к среднегодовой численности населения данной территории в расчете на 1000 чел. Если получаемые значения очень малы, то делают расчет на 10 000 человек. Так, по состоянию на 1987 г. имеем в целом по стране Крожд. = 19,8 ‰, Кест.прирост = 9,9 ‰. В том числе по г. Новосибирску Крожд. = 15,2 ‰, Ксм.= 9,1 ‰, Кбрачности = 10,9 ‰, Кразв. = 5,2 ‰ и т.д. Относительными величинами интенсивности выступают, например, показатели выработки продукции в единицу рабочего времени, затрат на единицу продукции, трудоемкости, эффективности использования производственных фондов и т.д., поскольку их получают сопоставлением разноименных величин, относящихся к одному и тому же явлению и одинаковому периоду или моменту времени. Метод расчета относительных величин интенсивности применяется при определении средних уровней (среднего уровня выработки, средних затрат труда, средней себестоимости изделий, средней цены и т.д.). Поэтому распространено мнение, что относительные величины интенсивности – это один из способов выражения средних величин. |
