статика. статика.как считать моменты сил. Виды связей и их реакции Приведем примеры связей и их замены силами реакций связей
 Скачать 0.58 Mb. Скачать 0.58 Mb.
|
|
Виды связей и их реакции Приведем примеры связей и их замены силами реакций связей. Гладкая поверхность (рис.2.а): Если тело опирается на идеально гладкую поверхность, то реакция поверхности направлена по нормали к общей касательной поверхностей тел в точке соприкосновения. Такая реакция называется нормальной реакцией. Подвижная шарнирная опора, подвижный шарнир – опора, поставленная на катки, не препятствующие перемещению тела параллельно опорной плоскости. Реакция подвижного цилиндрического шарнира направлена по нормали к поверхности, на которую опираются катки шарнира (рис.2.б). Неподвижная шарнирная опора, неподвижный цилиндрический шарнир – совокупность неподвижного валика и надетой на него втулки с твердым телом, вращающимся вокруг оси валика (подшипник, петля). Реакция неподвижного цилиндрического шарнира проходит через ось валика, в неизвестном направлении, поэтому определяют две ее составляющие, направленные параллельно осям координат, перпендикулярных оси валика (рис. 2.в). Жесткая заделка – жестко закрепленная балка, стержень. Связь препятствует любому движению конца балки. Для определения реакции жесткой заделки необходимо определить составляющие главного вектора RА, направленные параллельно осям координат и главный момент МА заделки (рис. 2.г). Стержень – жесткий невесомый стержень, концы которого соединены с другими частями конструкции шарнирами. Если тело закреплено с помощью стержня, то реакция направлена по линии, проведенной через опорные шарниры стержня (рис. 2.д). Гибкая связь – нить, цепь, канат, трос. Реакция приложена к твердому телу в точке соприкосновения и направлена по связи (рис. 2.е). 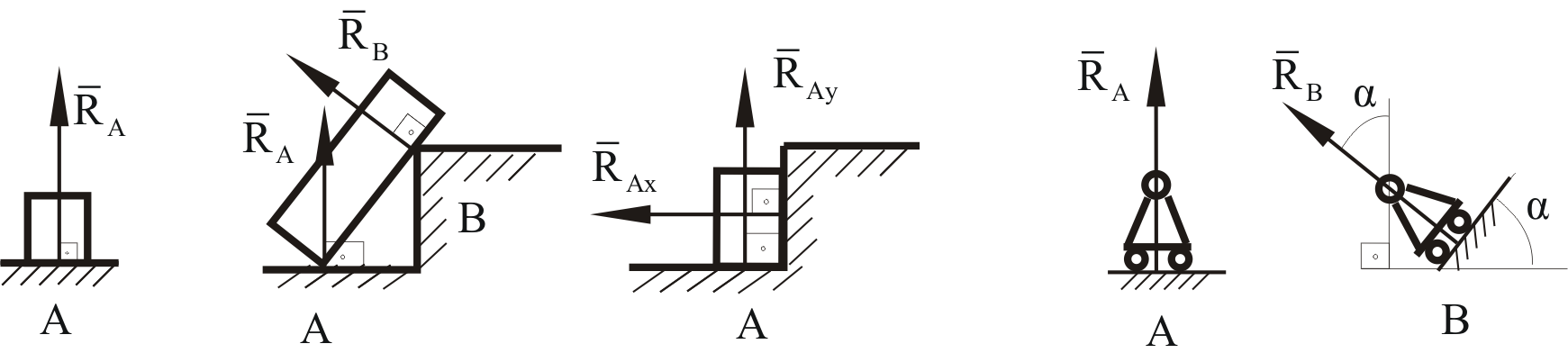 а) б)  в) г) д) е) Рис.2. Некоторые виды связей и их реакции а) гладкая поверхность, б) подвижная шарнирная опора, в) неподвижная шарнирная опора, г) жесткая заделка, д) стержень, е) гибкая связь Основные виды нагрузок В задачах курса теоретической механики встречаются следующие основные виды нагрузок (активных сил): сосредоточенные силы, распределенные нагрузки, нагрузки парой сил. 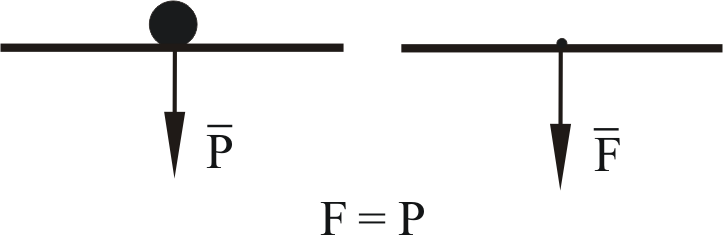 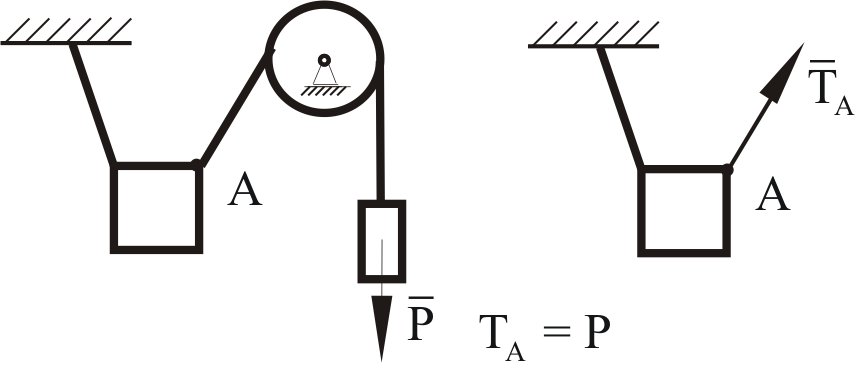 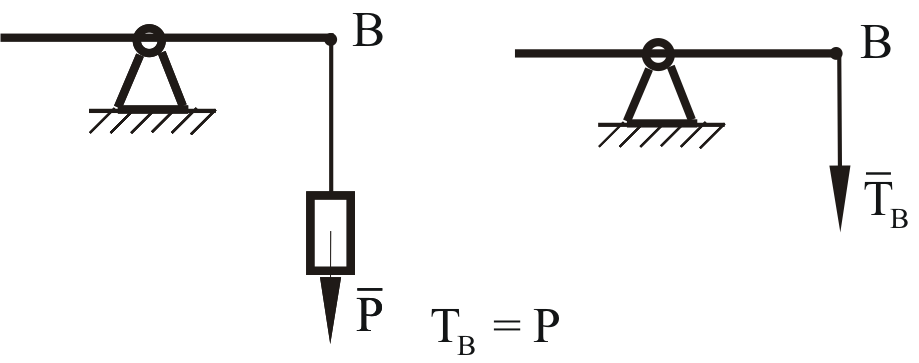 а) 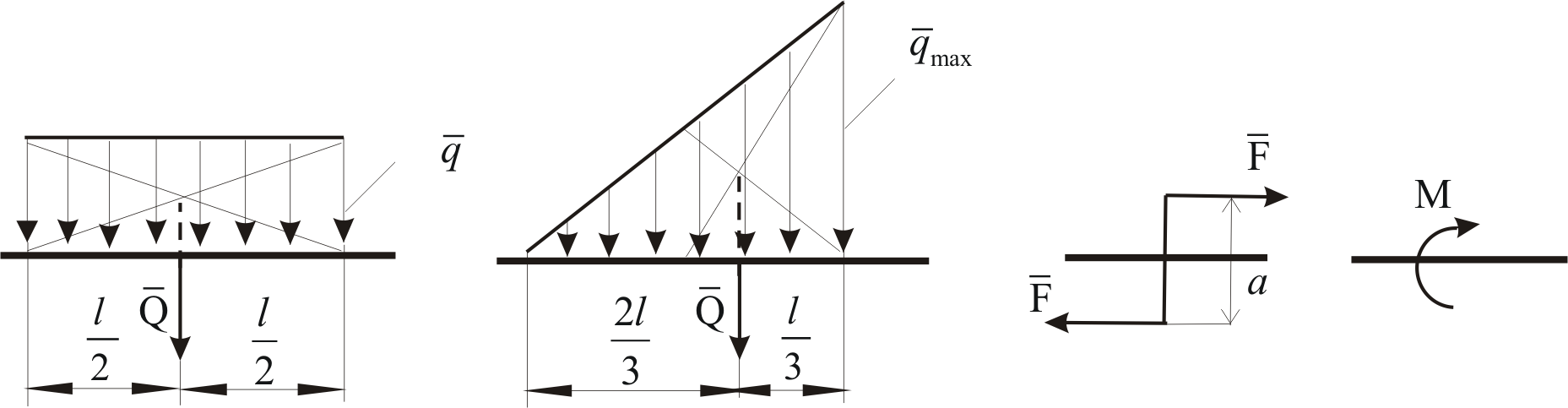 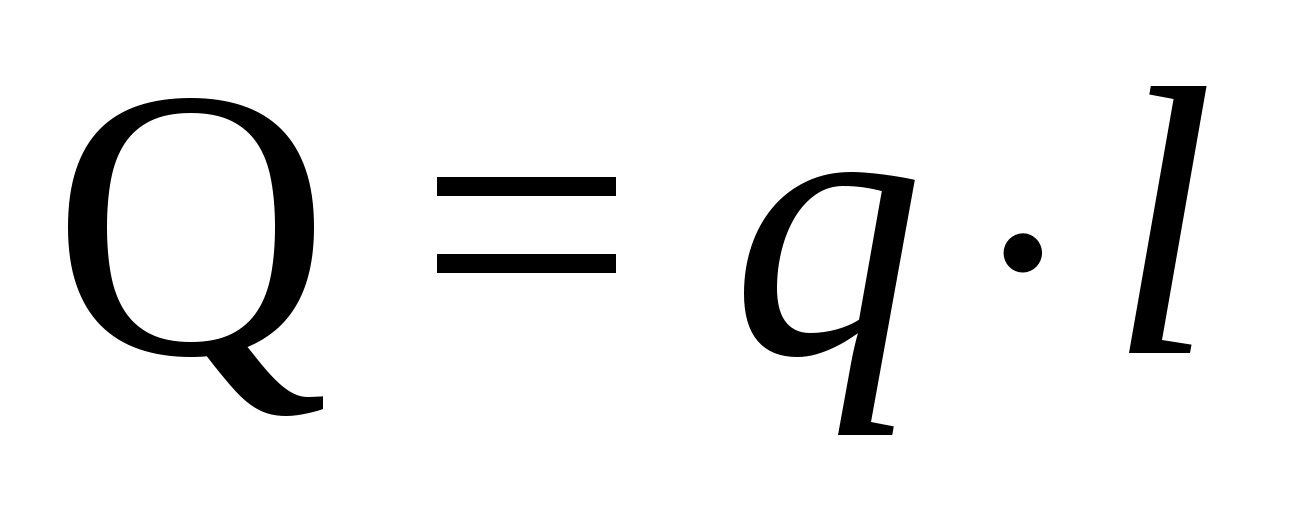 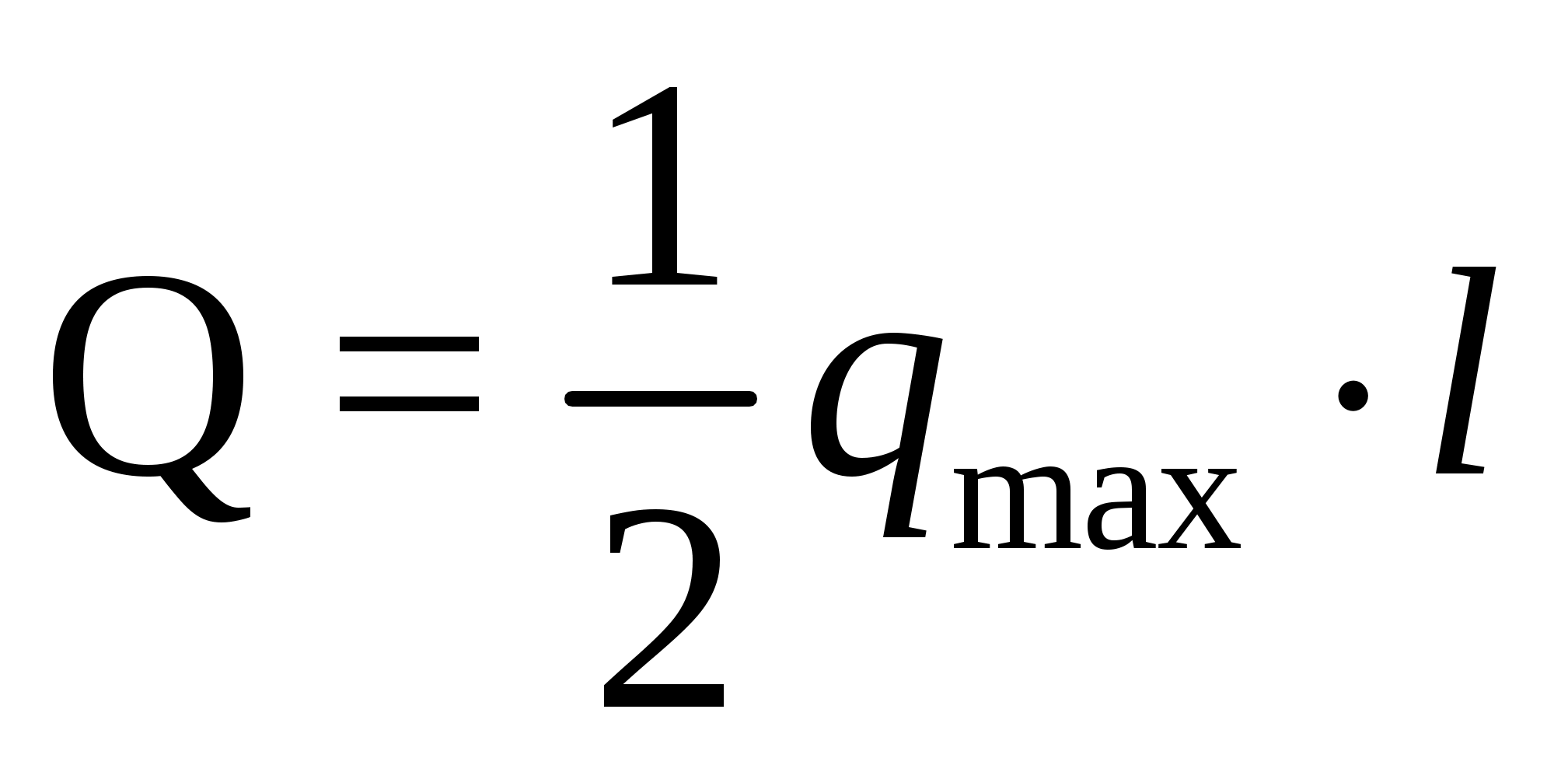 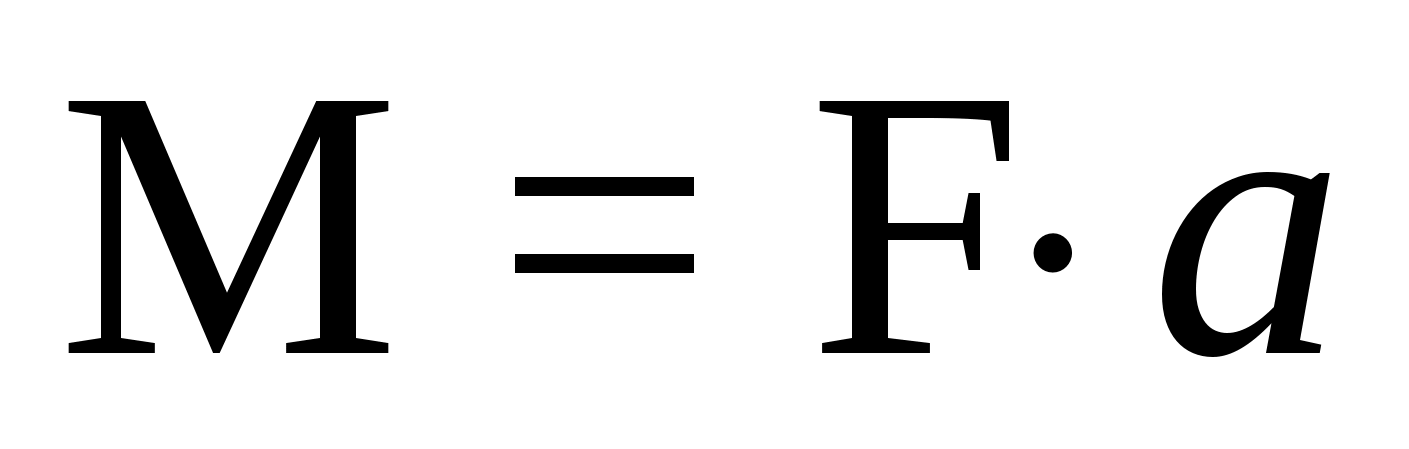 б) в) г) Рис.3. Основные виды нагрузок а) действие груза весом Р, б) равномерно-распределенная нагрузка интенсивностью q, в) нагрузка, распределенная по линейному закону с максимальным значением qmax, г) нагрузка парой сил 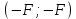 Сосредоточенные силы – силы, которые накладываются на участок поверхности тела, причем площадь участка очень мала по сравнению с размерами тела. Такие силы считаются приложенными к одной точке поверхности. Действие груза заменяется силой, равной весу груза и прикладывается в точке его приложения к твердому телу (рис.3.а). В случае наложения нагрузки через гибкую связь (нить), связь и груз заменяются силой натяжения связи (нити), равной весу груза (рис.3.а). Распределенные нагрузки – нагрузки, которые действуют на некотором участке площади или линии поверхности тела. Распределенные нагрузки характеризуются интенсивностью 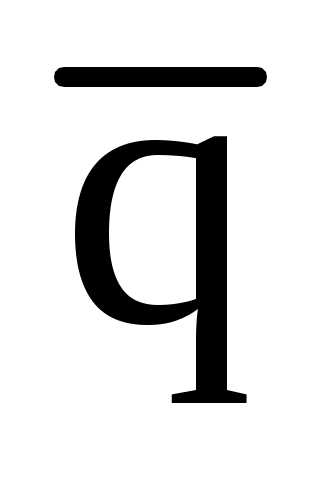 , то есть силой, отнесенной к единице длины или площади. Равномерно-распределенная нагрузка имеет одинаковую интенсивность по всему участку приложения (рис.3. б). В задачах, разобранных ниже, рассматриваются равномерно-распределенные нагрузки и нагрузки, распределенные по линейному закону. , то есть силой, отнесенной к единице длины или площади. Равномерно-распределенная нагрузка имеет одинаковую интенсивность по всему участку приложения (рис.3. б). В задачах, разобранных ниже, рассматриваются равномерно-распределенные нагрузки и нагрузки, распределенные по линейному закону.Распределенную нагрузку при решении задач следует заменить сосредоточенной силой, направленной параллельно заданной нагрузке в сторону ее действия. Величина сосредоточенной силы численно равна площади эпюры распределения нагрузки, а точка приложения находится под центром тяжести площади этой эпюры (рис.3.б, в). Нагрузка парой сил – нагрузка системой двух равных по модулю, параллельных и противоположно направленных сил (рис.3.г). Пару сил при решении заменяют алгебраическим моментом (см. п. 1.4), показывая на схеме его направление. Проекция силы на ось Если дана сила 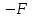 (рис.4), то ее можно разложить на составляющие по координатным осям Ох и Оу: (рис.4), то ее можно разложить на составляющие по координатным осям Ох и Оу: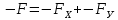 , (1) , (1)где 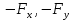 – составляющие силы – составляющие силы 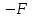 по координатным осям. по координатным осям.Составляющие силы по координатным осям это величины векторные. 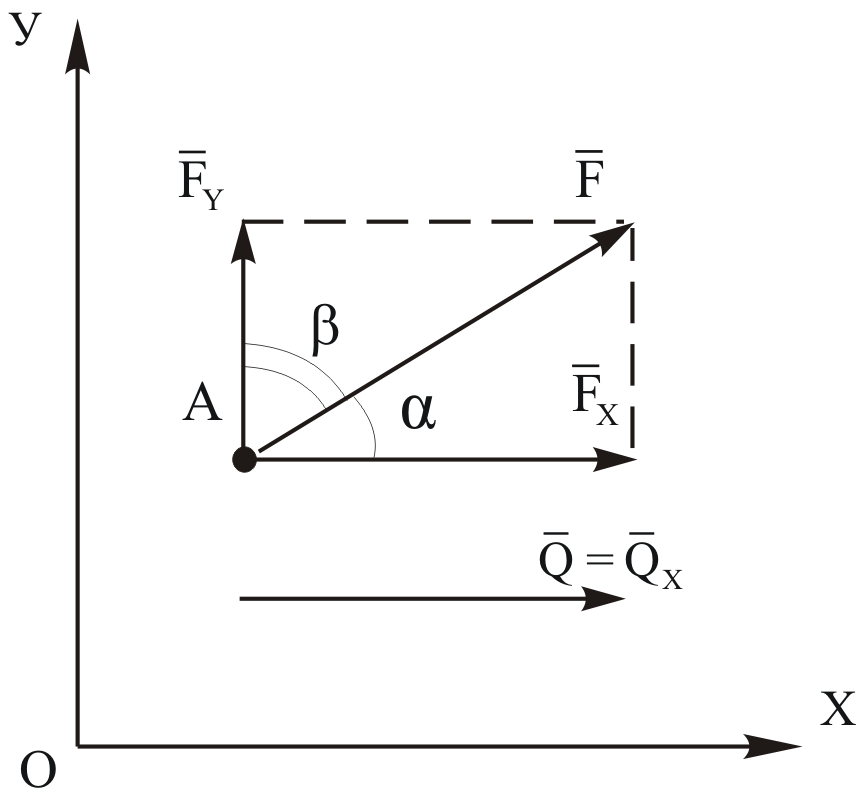 Рис.4. Разложение силы на составляющие по координатным осям Проекция силы на ось – алгебраическая величина, равная произведению модуля силы на косинус угла между направлением силы и положительным направлением оси: 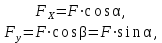 (2) (2)где α – угол, который образует сила 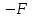 с положительным направлением осей Ох и Оу; с положительным направлением осей Ох и Оу;Fх , Fу – проекции силы 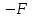 на координатные оси Ох и Оу. на координатные оси Ох и Оу.Модуль силы равен: 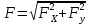 . (3) . (3)Проекция силы на ось положительна, если соответствующая составляющая силы направлена в положительную сторону оси, и отрицательна, если составляющая силы направлена в обратную сторону. Проекция силы на ось равна по модулю самой силе, если сила параллельна оси, и равна нулю, если сила перпендикулярна оси. Например, проекция силы 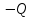 на ось Ох равна самой силе на ось Ох равна самой силе 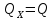 , а на ось Оу сила проецируется в точку, т.е. эта ее проекция равна нулю , а на ось Оу сила проецируется в точку, т.е. эта ее проекция равна нулю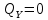 (рис.4). (рис.4).При решении задач рекомендуется вычислять абсолютное значение проекции силы как произведение модуля силы на косинус острого угла между линией действия силы и осью, определяя знак проекции по чертежу. Момент силы относительно точки. Теорема Вариньона. Алгебраический момент силы относительно точки равен произведению модуля силы на плечо, взятому со знаком плюс или минус. Плечо h силы относительноточки равно длине перпендикуляра, опущенного из точки на линию действия силы. Момент силы считается положительным, если сила стремится повернуть тело относительно моментной точки против хода часовой стрелки, и отрицательным – когда по ходу часовой стрелки. Для примера рассмотрим моменты сил 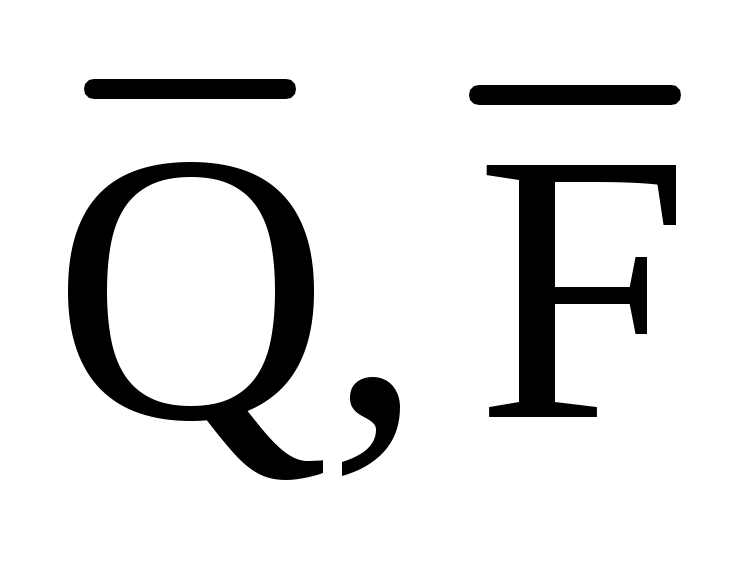 и и 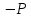 (рис.5). (рис.5).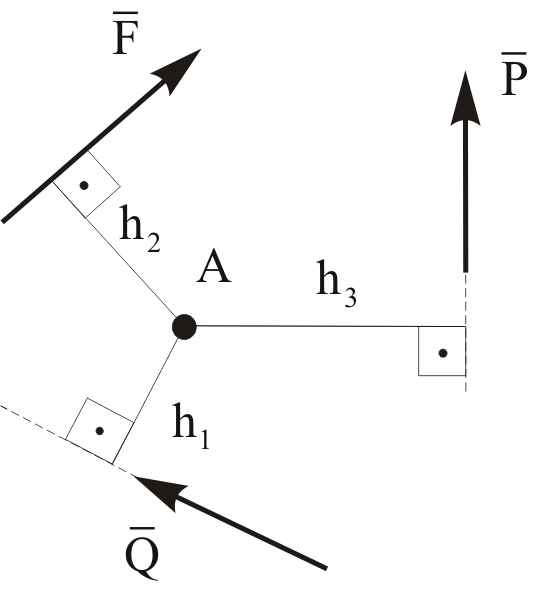 Рис.5. К нахождению момента силы относительно точки Моменты этих сил, относительно произвольной точки А, с учетом их знаков, будут равны: 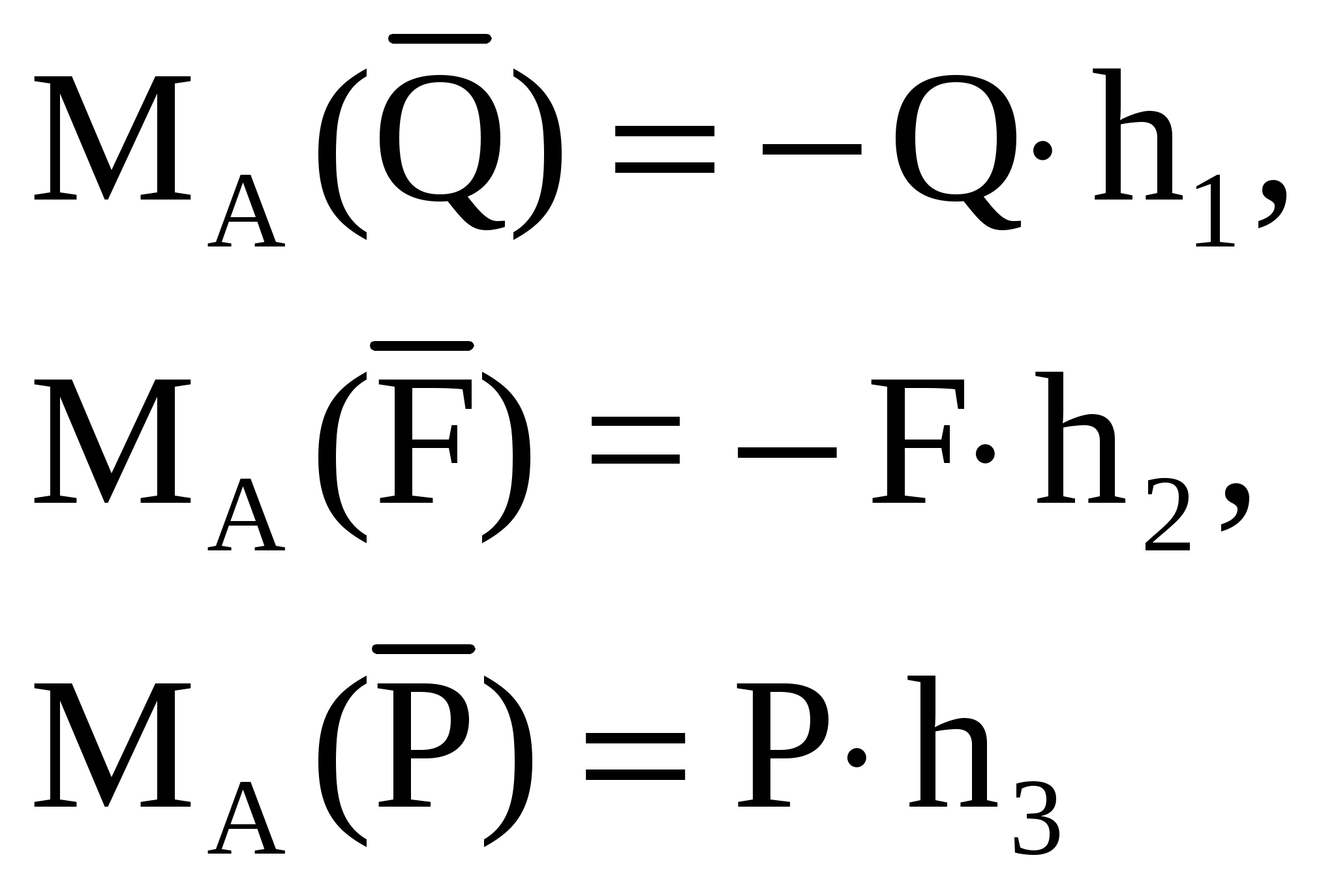 (4) (4)где h1 , h2 , h3 – плечи сил 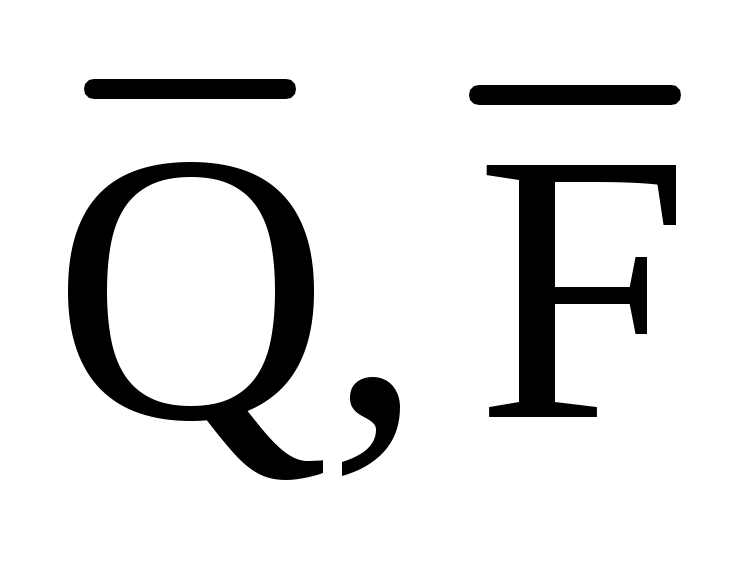 и и 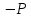 относительно точки А. относительно точки А.Алгебраический момент силы относительно точки равен нулю, если линия действия силы проходит через эту точку. Теорема Вариньона. Момент равнодействующей 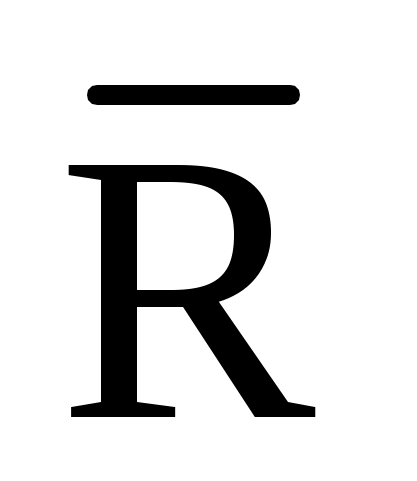 системы сил относительно произвольной точки равен сумме моментов сил этой системы, относительно этой же точки. системы сил относительно произвольной точки равен сумме моментов сил этой системы, относительно этой же точки.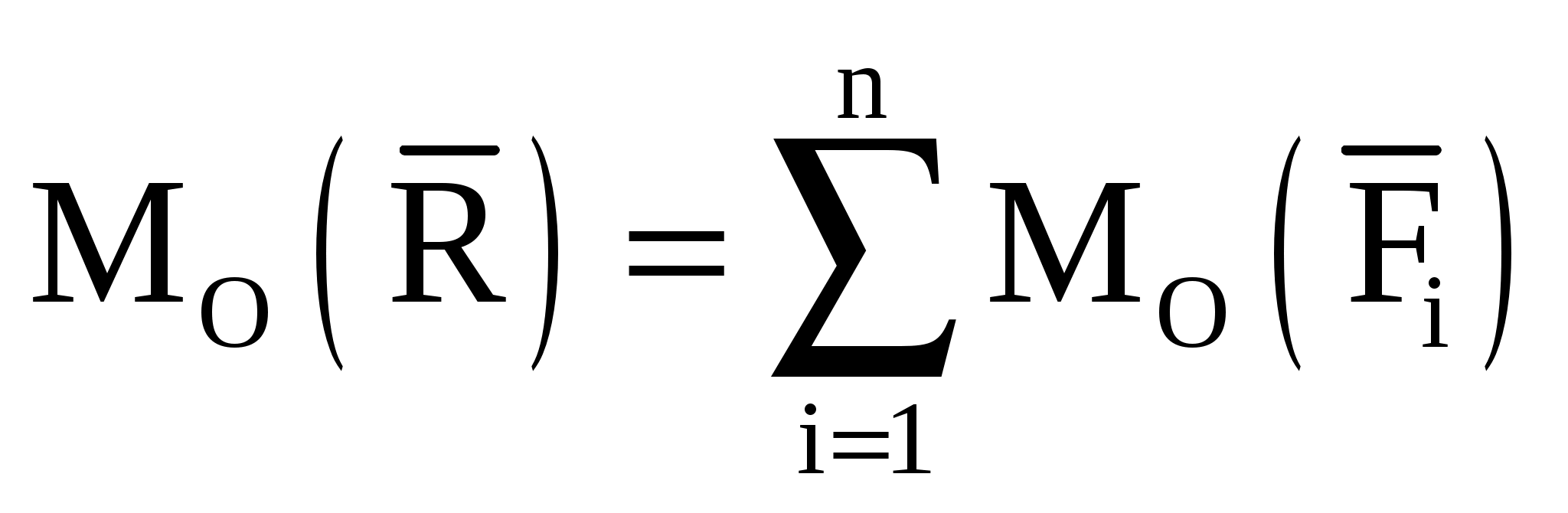 (5) (5)Иногда при решении задач вычисление плеча силы относительно точки трудоемко. В этих случаях удобно пользоваться теоремой Вариньона. Например, найдем момент силы  относительно точки О. Для этого необходимо разложить силу относительно точки О. Для этого необходимо разложить силу  на составляющие на составляющие 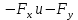 и найти их моменты относительно моментной точки О (рис.6). и найти их моменты относительно моментной точки О (рис.6).Согласно теореме 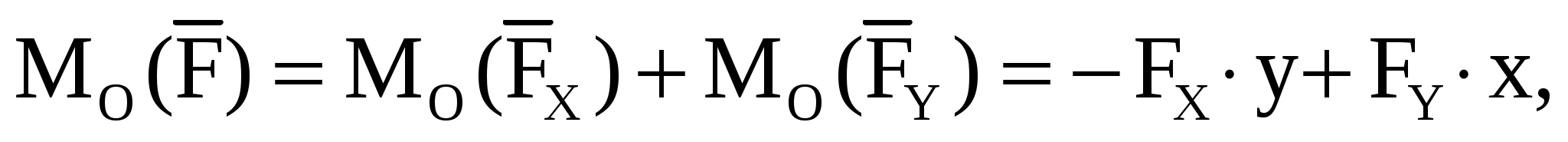 (6) (6)где х – плечо силы 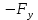 относительно точки О, относительно точки О,у – плечо силы 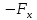 относительно точки О. относительно точки О.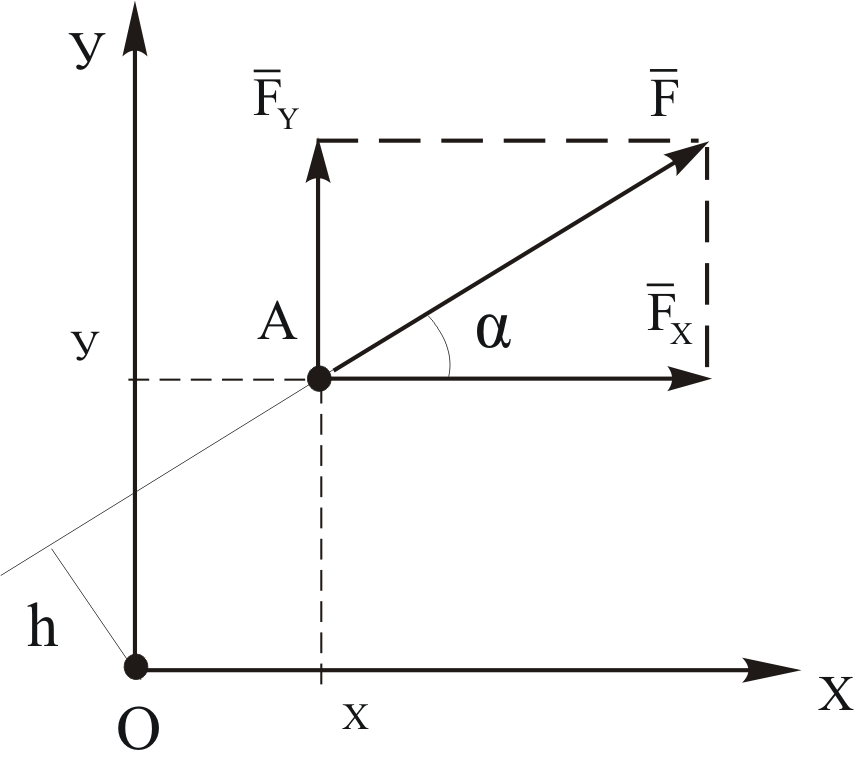 Рис.6.К теореме Вариньона Уравнения равновесия тела, находящегося под действием произвольной плоской системы сил Условия равновесия сил, произвольно расположенных на плоскости, можно выразить в виде системы трех уравнений, называемых основными уравнениями равновесия плоской системы сил: 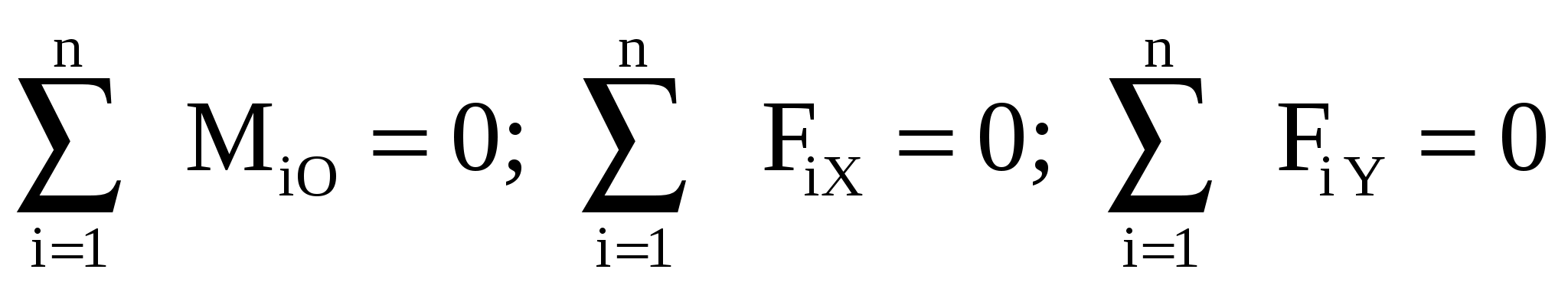 , (8) , (8) где 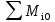 – главный момент системы относительно центра (точки) О, – главный момент системы относительно центра (точки) О,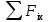 – проекция на ось Ох главного вектора системы, – проекция на ось Ох главного вектора системы,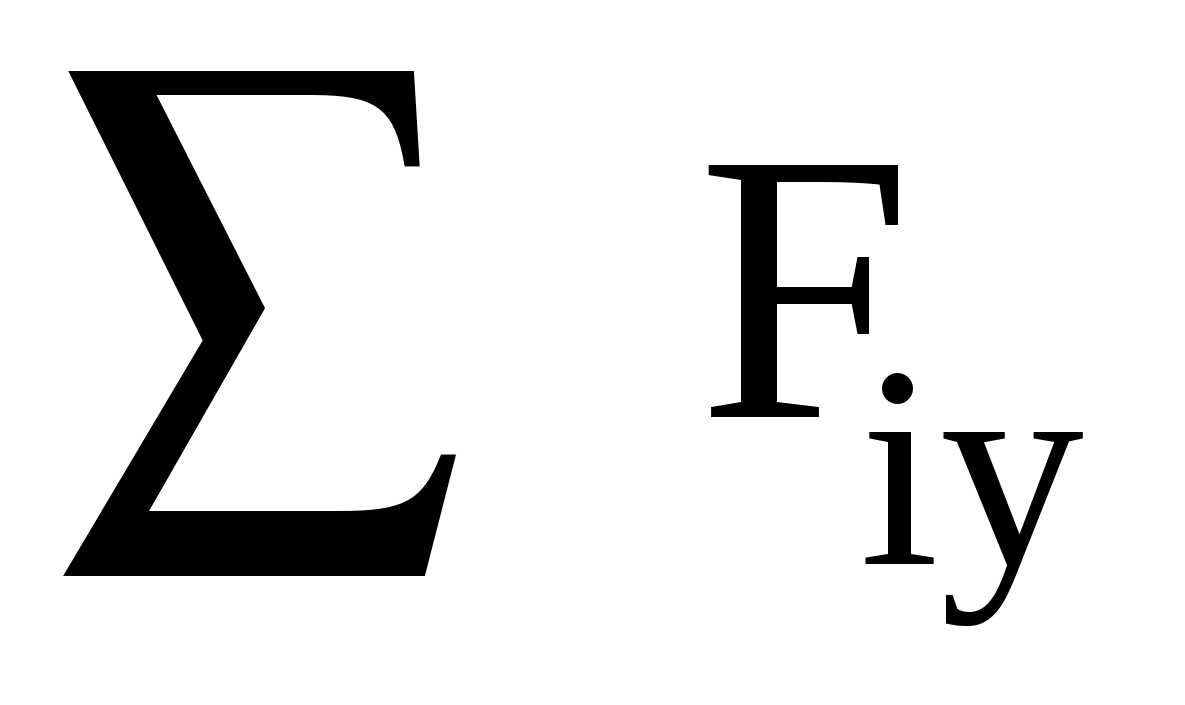 – проекция на ось Оу главного вектора системы. – проекция на ось Оу главного вектора системы.Для равновесия произвольной плоской системы сил, приложенной к твердому телу, необходимо и достаточно, чтобы суммы проекций всех сил на каждую из двух координатных осей и сумма их алгебраических моментов относительно любой точки, лежащей в плоскости действия сил, были равны нулю. Моментную точку и направление координатных осей можно выбирать произвольно, исходя из условий поставленной задачи. Существуют еще две системы трех уравнений равновесия произвольной плоской системы сил. Для равновесия произвольной плоской системы сил, приложенной к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил относительно двух любых точек (А и В), лежащих в плоскости действия сил, и алгебраическая сумма проекций этих сил на ось Ох, не перпендикулярную прямой, проходящей через точки А и В, были равны нулю: 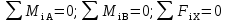 . (9) . (9) Для равновесия произвольной плоской системы сил, приложенной к твердому телу, необходимо и достаточно, чтобы суммы алгебраических моментов сил относительно трех любых точек (А, В и С), лежащих в плоскости действия сил и не лежащих на одной прямой, были равны нулю: 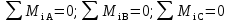 . (10) . (10) Статически определенными называют задачи, в которых число неизвестных не превышает числа уравнений равновесия сил. Для решения статически определенных задач плоской системы сил можно использовать любую систему трех уравнений равновесия. Статически неопределенными называют задачи, в которых число неизвестных превышает число уравнений равновесия сил. Эти задачи нужно решать с учетом деформации тела под действием внешних нагрузок. Решение таких задач выходит за рамки статики твердого тела и не рассматривается в данном разделе теоретической механики. Методические указания к решению задач на равновесие тела, находящегося под действием произвольной плоской системы сил В задачах статики обычно требуется определить реакции связей. Решение задач рекомендуется проводить в следующем порядке: 1. Построение расчетной схемы: 1). Выделить твердое тело (раму, стержень, ферму, балку), равновесие которого необходимо рассмотреть для определения неизвестных величин. 2). Изобразить активные силы, действующие на тело. Распределенную нагрузку на схеме заменить сосредоточенной силой и определить ее алгебраическое значение и точку приложения (см. п. 1.2). Для пары сил вычислить алгебраическое значение момента пары сил и показать на схеме направление его действия (см. п. 1.2, 1.4). В случае наложения активной силы через гибкую связь, связь и груз заменяются реакцией связи (например, натяжением нити), равной весу груза и направленной по связи (см. п. 1.2). 3). Заменить мысленно отброшенные связи соответствующими реакциями, изображая их на схеме (см. п. 1.1). Задать направление осей координат. 2. Решение задачи: 1). Составить уравнения равновесия твердого тела (см. п. 1.6). Уравнение моментов сил целесообразно составить относительно точки пересечения линий действия двух из неизвестных реакций. Сравнить число уравнений и число неизвестных – задача должна быть статически определимой. 2). Решить составленные уравнения равновесия, определив неизвестные величины. Отрицательное значение реакции показывает, что ее действительное направление противоположно выбранному и обозначенному на схеме. Для получения более простых уравнений равновесия следует за центр моментов выбирать точку, в которой пересекаются линии действия наибольшего числа неизвестных реакций, тогда моменты этих сил не войдут в уравнение моментов; при вычислении момента силы, имеющей составляющие по осям координат применять теорему Вариньона, вычислив сумму моментов составляющих сил относительно этой точки. Примеры решения задач Задача 1. Определить реакции опор рамы АСDВ (рис.8.а), находящейся под действием равномерно-распределенной нагрузки q=1,5кН/м, груза P= 2 кН, прикрепленного канатом к точке С, момента M=2 кН·м. Угол наклона каната к вертикали α =30°. Размеры рамы АС=3 м, CD=2 м, DB=1 м. 1. Построение расчетной схемы: 1). Изобразим раму АСDВ, равновесие которой необходимо рассмотреть для определения неизвестных величин. 2). Приложим к раме активные нагрузки 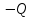 , М, Т=Р (рис.8.б). , М, Т=Р (рис.8.б).Распределенную нагрузку заменим сосредоточенной силой 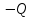 , приложенной в середине участка СD по направлению , приложенной в середине участка СD по направлению 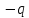 . Вычислим ее значение: . Вычислим ее значение: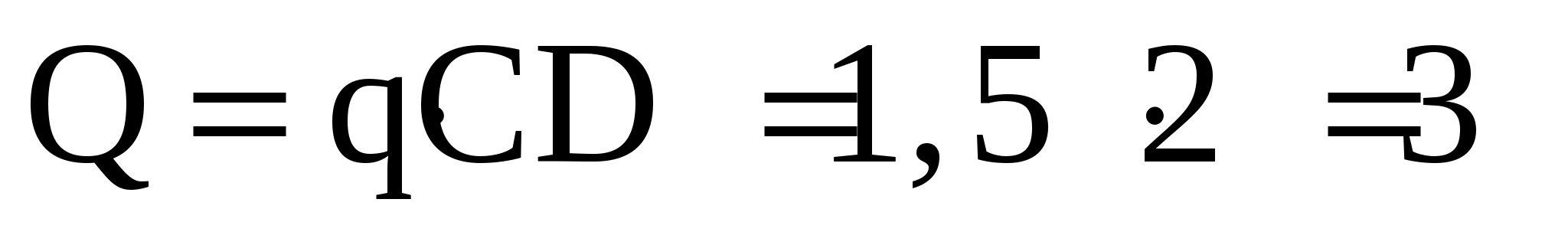 (кН). (кН).Действие груза Р заменим силой 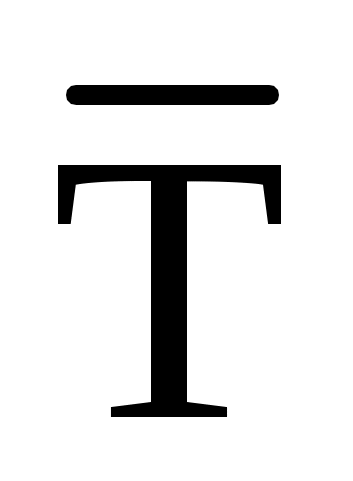 , равной по модулю весу груза и направленной по канату вниз, Т=Р. , равной по модулю весу груза и направленной по канату вниз, Т=Р.Покажем момент М пары сил. 3). Выберем направление координатных осей. Ось Сх – горизонтально вправо, Су – вертикально вверх. а) б) 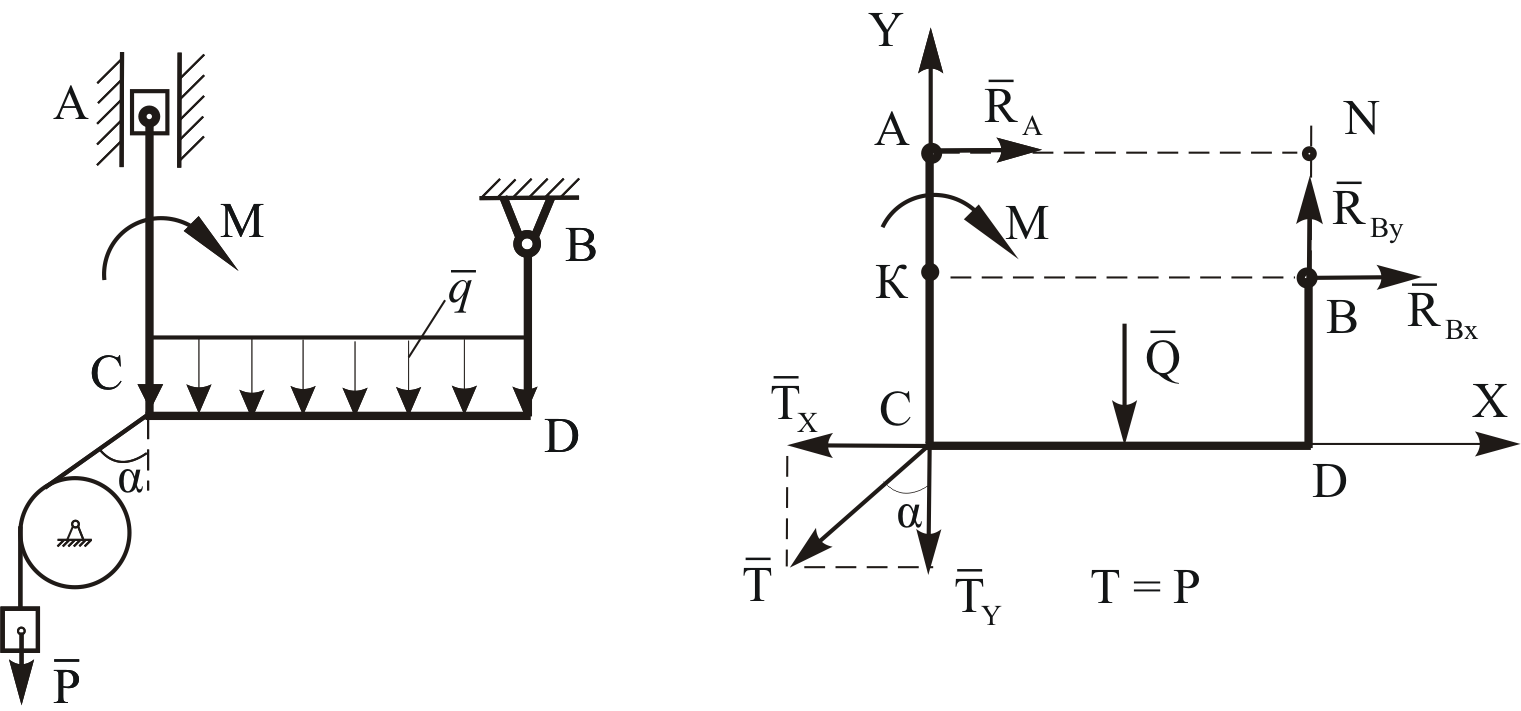 Рис.8. К задаче 1 а) схема рамы АСDВ, б) расчетная схема. 4). Заменим связи соответствующими реакциями. Реакция 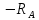 перпендикулярна направляющим ползуна; реакцию перпендикулярна направляющим ползуна; реакцию 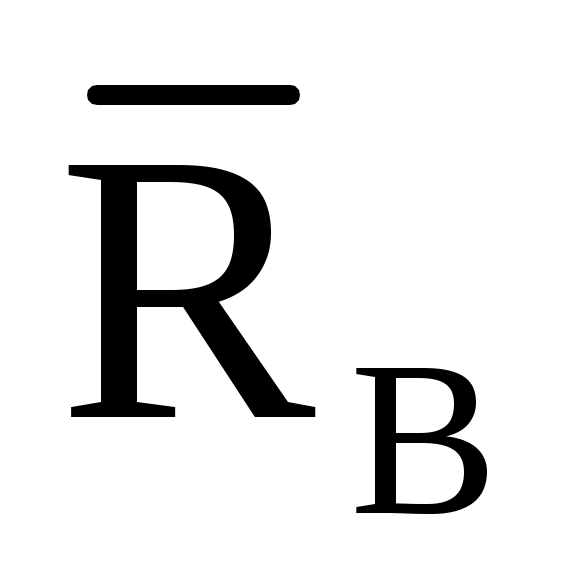 неподвижного шарнира представим составляющими неподвижного шарнира представим составляющими 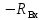 и и 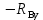 по осям координат, предполагая их положительными. по осям координат, предполагая их положительными.5). Разложим наклонную силу  на составляющие по координатным осям: на составляющие по координатным осям: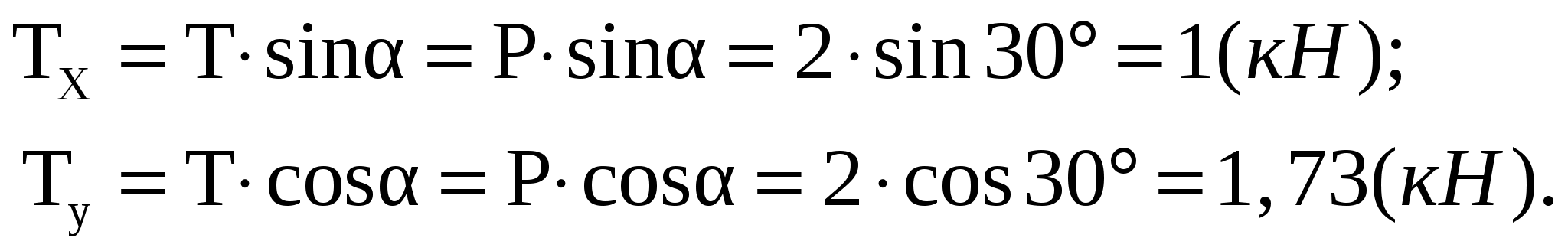 2. Решение задачи: 1). Составим уравнения равновесия плоской системы сил. За моментную точку примем точку В пересечения двух неизвестных реакций 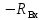 и и 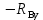 . .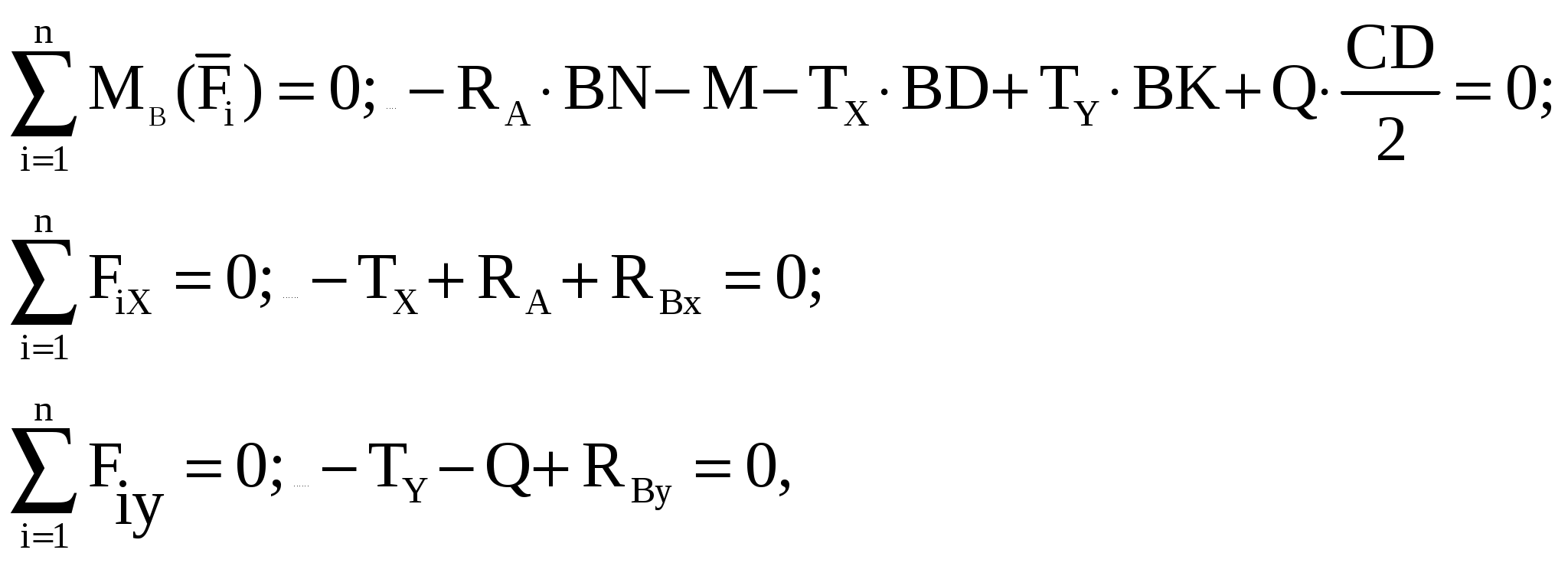 (11) (11)где 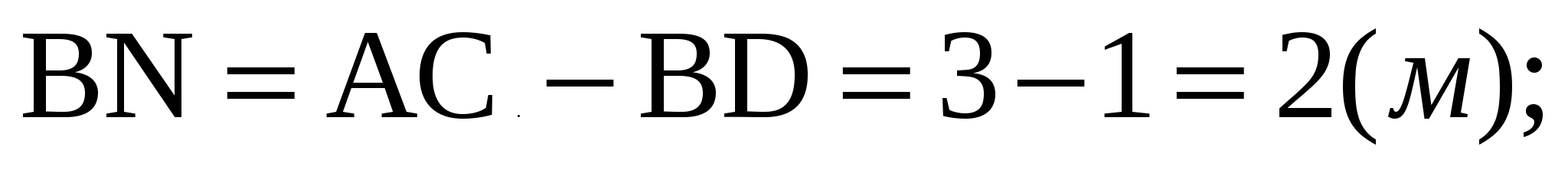 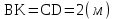 . .Задача является статически определимой, так как имеем три уравнения с тремя неизвестными 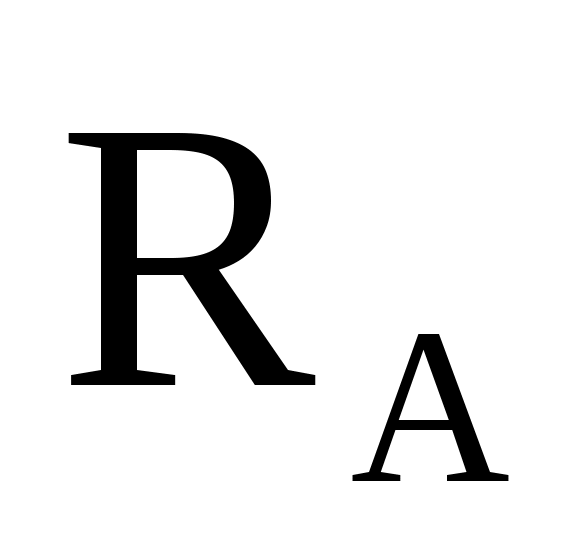 , , 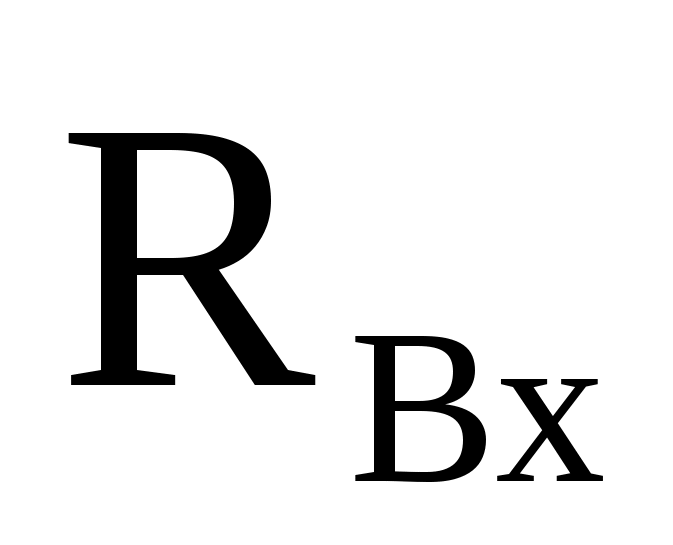 и и 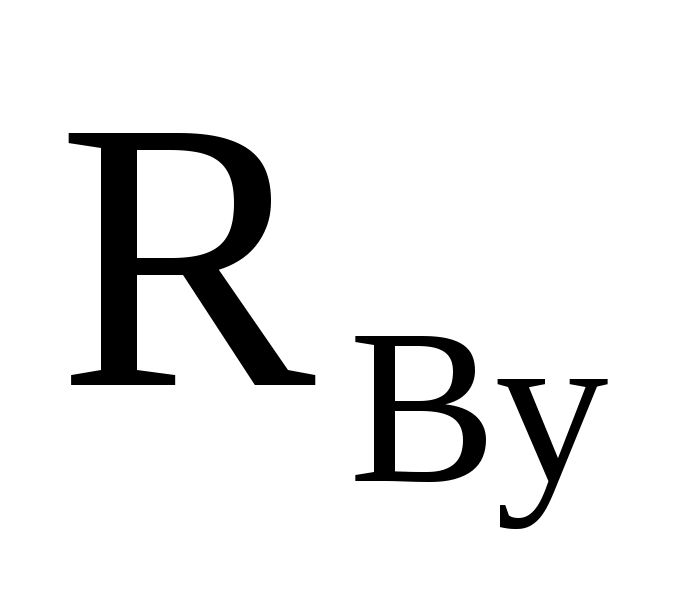 . .2). Решим составленные уравнения равновесия, определив реакции. Из первого уравнения системы (11) находим RA: 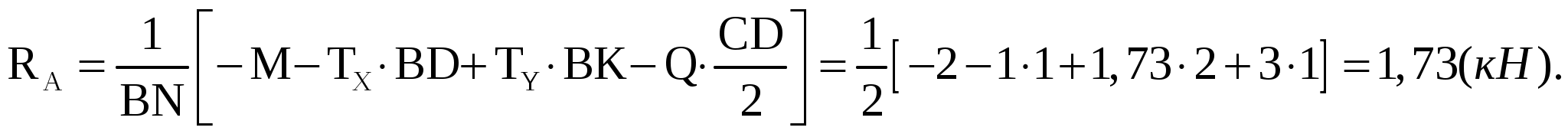 Из второго уравнения находим составляющую RВх: 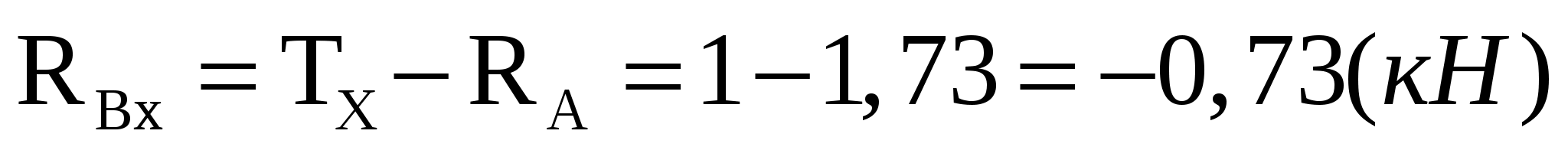 . .Из третьего – определим составляющую RВу: 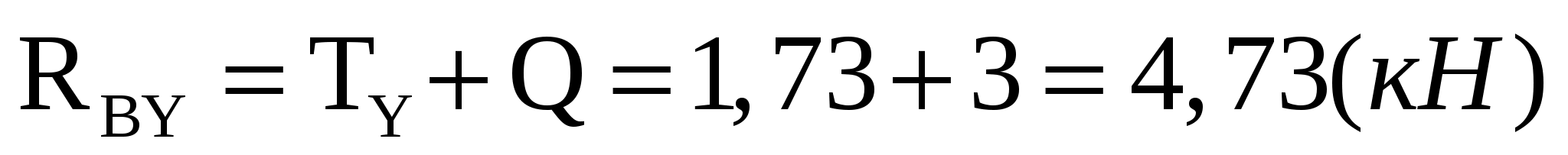 . .Отрицательное значение реакции 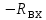 показывает, что ее действительное направление противоположно выбранному в начале решения. показывает, что ее действительное направление противоположно выбранному в начале решения. |
