ПРОЕКТИРОВАНИЕ РАБОЧЕЙ ПЛОЩАДКИ. Включая сварку проектирование рабочей площадки

• Название: Включая сварку проектирование рабочей площадки
• Анкор: ПРОЕКТИРОВАНИЕ РАБОЧЕЙ ПЛОЩАДКИ.doc
• Дата: 25.12.2017
• Размер: 3.55 Mb.
• Имя файла: ПРОЕКТИРОВАНИЕ РАБОЧЕЙ ПЛОЩАДКИ.doc
• Тип: Учебное пособие; #12935
• страница: 6 из 19

площадь пояса

;

площадь стенки

A_w = A– 2A_f = 17,4– 2 ∙ 5,48 = 6,44 см ²;

отношение

A_f/A_w = 5,48 / 6,44 = 0,85.

По табл. 4.2 определяем коэффициент с_x = 1,09.

Равномерно распределенная нагрузка от собственного веса балки настила длиной 1 м



Нормативная нагрузка на балку настила



Расчетная нагрузка



Изгибающий момент



Поперечная сила



Проверка несущей способности балки. Проверка прочности по нормальным напряжениям в середине балки:



Проверка прочности по касательным напряжениям у опоры:

Общую устойчивость балок настила проверять не надо, поскольку их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним стальным сплошным настилом.

Проверка жесткости. Прогибы, определяемые от нормативных нагрузок, не должны превышать их предельных значений, установленных нормами проектирования. Для однопролетной балки, нагруженной равномерно распределенной нагрузкой, проверка прогиба производится по формуле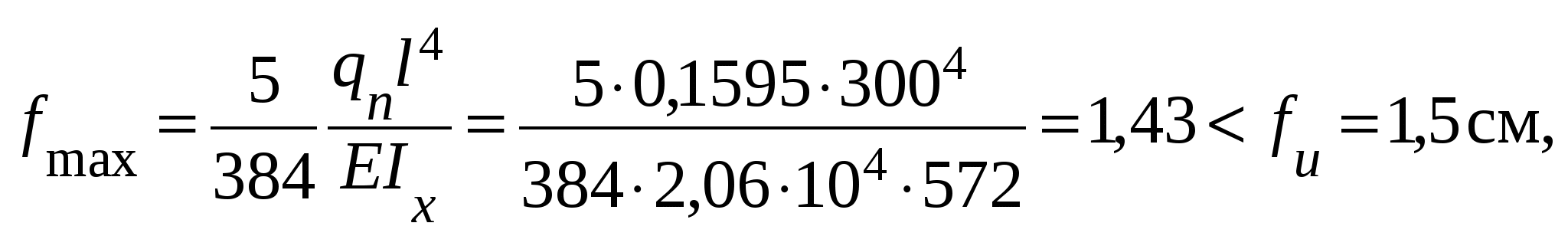



где f_u = l/200 = 1,5 см при пролете l= 3 м (см. табл. 4.1).

Принятое сечение удовлетворяет условиям прочности и жесткости.

Определяем вес балки настила на 1м² рабочей площадки:

g_n,бн = 13,7/a₁ = 13,7 / 1,2 = 11,42 кг/м² = 0,114 кН/м².

4.2.2. Расчет вспомогательной балки

Расчетная схема вспомогательной балки представлена на рис. 4.8.

Пролет вспомогательной балки l= 6 м.


Рис. 4.8. Расчетная схема вспомогательной балки (2-й вариант)

Нагрузка на вспомогательную балку передается от балок настила в виде сосредоточенных сил, равных двум опорным реакциям этих балок. При частом расположении балок настила (шаг а₁  l/5, т.е. при числе сосредоточенных сил, попадающих на вспомогательную балку, более четырех) сосредоточенная нагрузка заменяется равномерно распределенной, собираемой с соответствующей грузовой площади (рис.4.2).

Проверяем: (а₁ = 1,2 м) = (l/5= 6 / 5 = 1,2 м). Принимаем нагрузку в виде равномерно распределенной.

Нормативная нагрузка на вспомогательную балку

_{qn = a2(pn + gn,н+ gn,бн) = 3 (12,55 + 0,628 + 0,114) = 39,88 кН/м.}

Расчетная нагрузка

q = a₂(p_nγ_fp + g_n,нγ_{fg +} g_n,бнγ_fg) =

= 3 (12,55 · 1,2 + 0,628 · 1,05 + 0,114 · 1,05) = 47,52 кН/м.

Расчетный изгибающий момент

M_max = ql²/8 = 47,52 ∙ 6² / 8 = 213,84 кН∙м.

Максимальная поперечная сила у опоры



Требуемый момент сопротивления

W_n,min = M_max/(c_xβR_yγ_c) = 21384 / (1,12 · 1 · 24 · 1) = 795,54 см³,

По сортаменту выбираем ближайший номер двутавра, у которого W_x > W_n,min. Принимаем I40, имеющий момент сопротивления W_x= 953 см³; момент инерции сечения I_x= 19062 см⁴; статический момент полусечения S_x = 545 см³; площадь сечения А = 72,6 см²; ширину пояса b_f = 155 мм; толщину пояса t_f = 13 мм; толщину стенки t_w = 8,3 мм; радиус внутреннего закругления R= 15 мм; линейную плотность (массу 1 м пог.) 57 кг.

Уточнение коэффициента с_x, M и Q с учетом собственного веса вспомогательной балки.

Площадь пояса

Площадь стенки



Отношение A_f/A_w = 20,15 / 32,3 = 0,62.

По табл. 4.2 определяем коэффициент с_x = 1,108.

Равномерно распределенная нагрузка от собственного веса вспомогательной балки



Нормативная нагрузка на вспомогательную балку



Расчетная нагрузка

_{q = 47,52 + qn,вбγfg = 47,52 + 0,57 ∙ 1,05 = 48,12 кН/м.}

Расчетный изгибающий момент

M_max = ql²/8 = 48,12 · 6² / 8 = 216,54 кН∙м.

Поперечная сила



Проверка несущей способности балки. Проверка прочности по нормальным напряжениям в середине балки:



Резерв несущей способности



Несмотря на большое недонапряжение сечение принято, так как при изменении сечения в меньшую сторону, принимая ближайший профиль I36 сW_x = 743 см³, перенапряжение составит 9%.

Проверка прочности по касательным напряжениям вблизи опоры: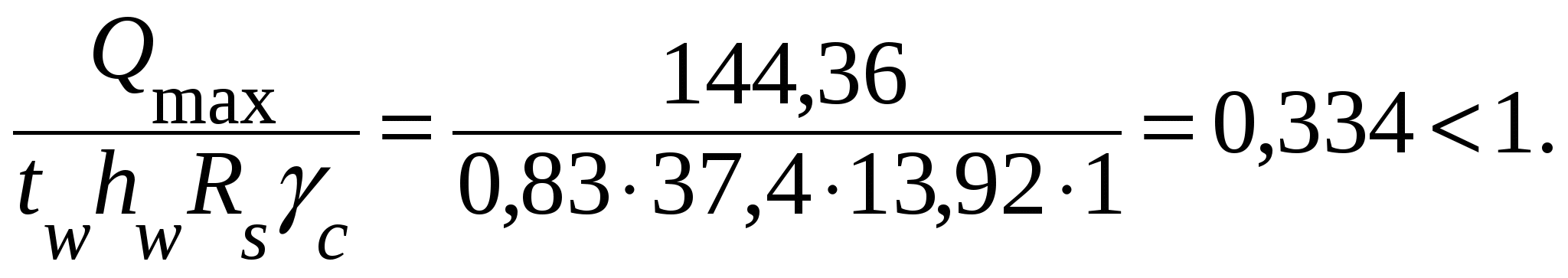



В местах приложения локальной нагрузки к верхнему поясу (рис. 4.9), а также в опорных сечениях балки, не укрепленных ребрами жесткости, стенку следует дополнительно проверить на местное напряжение σ_loc по формуле



где σ_loc = F/(l_eft_w) = 57,04 / (12,9 · 0,83) = 5,33 кН/см² ,

здесь F= 2Q = 2 · 28,52 = 57,04 кН – расчетное значение сосредоточенной силы, равное двум реакциям от балок настила;

l_ef = b + t_f′ = 7,3 + 2 · 2,8 = 12,9 см – условная длина распределения сосредоточенной нагрузки на стенку вспомогательной балки;

b = 73 мм – ширина пояса балки настила;

t'_f= t_f + R = 13 + 15 = 28 мм – расстояние от наружной грани полки до начала внутреннего закругления стенки.



Рис. 4.9. Схема распределения сосредоточенной нагрузки

на стенку прокатной балки

Общую устойчивость вспомогательных балок проверять не надо, поскольку их сжатые пояса надежно закреплены в горизонтальном направлении часто расположенными и приваренными к ним балками настила.

Проверка жесткости. Прогибы, определяемые от нормативных нагрузок, не должны превышать их предельных значений, установленных нормами проектирования. Для однопролетной балки, нагруженной равномерно распределенной нагрузкой, проверка прогиба производится по формуле



где f_u = l/250 = 2,4 см при пролете l= 6 м (см. табл. 4.1).

Принятое сечение удовлетворяет условиям прочности и жесткости.

Определяем вес вспомогательной балки на 1м² рабочей площадки:



4.3. Третий вариант балочной клетки

Тип балочной клетки – нормальный (рис. 4.10).

Настил – железобетонный.

Балки настила приняты с шагом а₁ = 3 м.



Рис. 4.10. Третий вариант балочной клетки

4.3.1. Расчет железобетонного настила

При использовании в качестве несущего настила железобетонных плит при принятом расчетном пролете плитыl_пл, равном шагу балок настила, толщину плиты выбираем по табл. 4.4 в зависимости от полезной нормативной нагрузки p_n. Расчетный пролет плиты (шаг балок) в различных рассматриваемых вариантах принимают в пределах от 1,2 до 3 м.

Таблица 4.4

Толщина железобетонной плиты

Расчетный пролет плиты lн, м	Толщина железобетонной плиты, см, при временной нормативной нагрузке pn, кН/м2
	10 – 15	15 – 20	20 – 25	25 – 30	30 – 35
<1,5	8	8	10	12	14
1,5 – 2,0	10	10	12	12	14
2,1 – 2,5	10	12	12	14	16
2,6 – 3,0	12	14	14	16	18

Задавшись расчетным пролетом плиты l_пл = а₁ = 3 м (могут быть другие варианты), принимаем толщину плиты t_пл = 12 см при нормативной полезной нагрузке p_n = 12,55 кН/м².

Нормативная нагрузка от веса железобетонной плиты (при плотности железобетона ρ = 2500 кг/м³)



4.3.2. Расчет балки настила

Расчетная схема балки настила представлена на рис. 4.11. Пролет балки настила l = B = 6 м.



Рис. 4.11. Расчетная схема балки настила (3-й вариант)
Определяем нормативную и расчетную нагрузки.

Нормативная нагрузка на балку принимается равномерно распределенной:



Расчетная нагрузка



где _g = 1,1 – коэффициент надежности по нагрузке для постоянной нагрузки от железобетонных плит.

Расчетный изгибающий момент



Максимальная поперечная сила



Требуемый момент сопротивления поперечного сечения балки при работе с учетом упругопластических деформаций

W_n,min = M_max/(c_xβR_yγ_c) = 24786 / (1,12 · 1 · 24 · 1) = 922,1 см³,

По сортаменту выбираем ближайший номер двутавра, у которого W_x> W_n,min. Принимаем I40, имеющий момент сопротивления W_x = 953 см³; статический момент полусечения S_x = 545 см³; момент инерции сечения I_x = 19062 см⁴; площадь сечения А = 72,6 см²; ширину пояса b_f = 155 мм; толщину пояса t_f = 13 мм; толщину стенки t_w= 8,3 мм; линейную плотность (массу 1 м пог.) 57 кг/м.

Уточнение коэффициента с_x, M и Q c учетом собственного веса балки настила.

Площадь пояса



Площадь стенки



Отношение

A_f/A_w = 20,15 / 32,3 = 0,62.

По табл. 4.2 определяем коэффициент с_x = 1,108.

Равномерно распределенная нагрузка от собственного веса балки настила длиной 1 м

q_n,бн = 57 кг/м = 0,57 кН/м.

Нормативная нагрузка на балку настила



Расчетная нагрузка



Расчетный изгибающий момент



Максимальная поперечная сила



Проверка несущей способности балки. Проверка прочности по нормальным напряжениям в середине балки:



Резерв несущей способности



Проверка прочности по касательным напряжениям у опоры: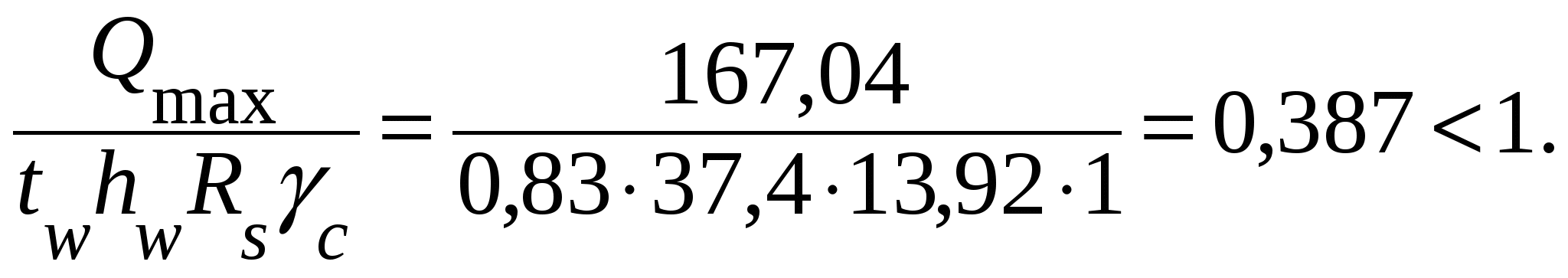



Общую устойчивость балок настила проверять не надо, поскольку их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним железобетонным настилом.

Проверка жесткости. Прогибы, определяемые от нормативных нагрузок, не должны превышать их предельных значений, установленных нормами проектирования. Для однопролетной балки, нагруженной равномерно распределенной нагрузкой, проверка прогиба производится по формуле



где при пролете l= 6 м (см. табл. 4.1).

Принятое сечение удовлетворяет условиям прочности и жесткости.

В случае невыполнения любого из условий необходимо изменить сечение, приняв по сортаменту следующий номер двутавра и вновь проверить прочность и жесткость балки.

Определяем вес балки настила на 1м² рабочей площадки:



4.4. Четвертый вариант балочной клетки

Тип балочной клетки – усложненный (рис. 4.12).

Настил – железобетонный.

Балки настила приняты с шагом а₁ = 2 м.

Вспомогательные балки с шагом а₂ = 4,5 м.



Рис. 4.12. Четвертый вариант балочной клетки

4.4.1. Расчет балки настила

При использовании в качестве настила железобетонных плит их толщину принимаем t_пл = 10 см по табл. 4.4 (в зависимости от расчетного пролета плиты l_н = а₁ = 2 м и полезной нормативной нагрузки p_n = 12,55 кН/м²). Нормативная нагрузка от веса железобетонной плиты

g_п,н = t_пл ρ = 0,1 ∙ 2500 = 250 кг/м² = 2,5 кН/м².

Расчетная схема балки настила представлена на рис. 4.13.



Рис. 4.13. Расчетная схема балки настила (4-й вариант)

Пролет балки настила l = a₂ = 4,5 м.

Определяем нормативную и расчетную нагрузку.

Нормативная нагрузка на балку принимается равномерно распределенной:



Расчетная нагрузка



где _g = 1,1 – коэффициент надежности по нагрузке для постоянной нагрузки от железобетонных плит.

Расчетный изгибающий момент



Максимальная поперечная сила



Требуемый момент сопротивления поперечного сечения балки при работе с учетом упругопластических деформаций

W_n,min = M_max/(c_xβR_yγ_c) = 9016 / (1,12 · 1 · 24 · 1) = 335, 4 см³,

По сортаменту выбираем ближайший номер двутавра, у которого W_x> W_n,min. Принимаем I27, имеющий момент сопротивления W_x = 371 см³; статический момент полусечения S_x = 210 см³; момент инерции сечения I_x = 5010 см⁴; площадь сечения А = 40,2 см²; ширину пояса b_f = 125 мм; толщину пояса t_f = 9,8 мм; толщину стенки t_w= 6 мм; линейную плотность (массу 1 м пог.) 31,5 кг/м.

Уточнение коэффициента с_x, M и Qc учетом собственного веса балки настила.

Площадь пояса



Площадь стенки



Отношение

A_f/A_w = 12,25 / 15,7 = 0,78.

По табл. 4.2 определяем коэффициент с_x = 1,09.

Равномерно распределенная нагрузка от собственного веса балки настила длиной 1 м



Нормативная нагрузка на балку настила



Расчетная нагрузка



Расчетный изгибающий момент



Максимальная поперечная сила



Проверка несущей способности балки. Проверка прочности по нормальным напряжениям в середине балки:



Резерв несущей способности



Проверка прочности по касательным напряжениям у опоры:

Общую устойчивость балок настила проверять не надо, поскольку их сжатые пояса надежно закреплены в горизонтальном направлении приваренным к ним железобетонным настилом.

Проверка жесткости. Прогибы, определяемые от нормативных нагрузок, не должны превышать их предельных значений, установленных нормами проектирования. Для однопролетной балки, нагруженной равномерно распределенной нагрузкой, проверка прогиба производится по формуле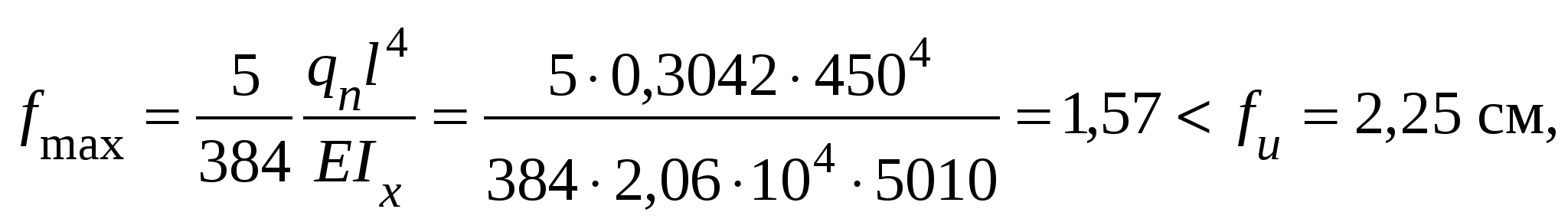



где f_u = l/200 = 2,25 см при пролете l= 4,5 м (см. табл. 4.1).

Принятое сечение удовлетворяет условиям прочности и жесткости.

Определяем вес балки настила на 1м² рабочей площадки:



4.4.2. Расчет вспомогательной балки

Расчетная схема вспомогательной балки представлена на рис. 4.14.

Пролет вспомогательной балки l= b= 6 м.

При (а₁ = 2 м) > (l/5= 6 / 5 = 1,2 м) принимаем нагрузку в виде сосредоточенных сил от двух реакций балок настила.

Нормативная сосредоточенная нагрузка на вспомогательную балку

F_n = q_na₂ = 30,42 · 4,5 = 136,89 кН,

где q_n– нормативная равномерно распределенная нагрузка на балку

настила.

Расчетная сосредоточенная нагрузка на вспомогательную балку

F= qa₂ = 35,95 · 4,5 = 161,78 кН,

Опорные реакции

R_a = R_b= 1,5F= 1,5 · 161,78 = 242,67 кН.



Рис. 4.14. Расчетная схема вспомогательной балки (4-й вариант)

Расчетный изгибающий момент

M_max = (R_a – F/2)a₁ = (242,67 – 161,78 / 2) ∙ 2= 323,56 кН·м.

Максимальная поперечная сила у опоры

Q_max = R_a – F/2 = 242,67 – 161,78 / 2 = 161,78 кН.

Требуемый момент сопротивления

W_n,min = M_max/(c_xmβR_yγ_c) = 32356 / (1,06 · 1 · 24 · 1) = 1271,86 см³,

где c_xm = 0,5 (1 + c_x) = 0,5 (1 + 1,12) = 1,06 – коэффициент, учитывающий развитие пластических деформаций при наличии зоны чистого изгиба.

По сортаменту выбираем ближайший номер двутавра, у которого

W_x>W_n,min. Принимаем I50, имеющий момент сопротивления W_x = 1589 см³; момент инерции сечения I_x= 39727 см⁴; статический момент полусечения S_x = 919 см³; площадь сечения А = 100 см²; ширину пояса b_f = 170 мм; толщину пояса t_f = 15,2 мм; толщину стенки t_w = 10 мм; радиус внутреннего закругления R= 17 мм; линейную плотность (массу 1пог. м) q_n,вб = 78,5 кг/м.

Уточнение коэффициента с_x, M и Q с учетом собственного веса вспомогательной балки.

Площадь пояса



Площадь стенки



Отношение

A_f/A_w = 25,84 / 48,32 = 0,53.

По табл.4.2 определяем коэффициент с_x = 1,12 и с_xm = 0,5 (1 + 1,12) = 1,06.

Расчетная равномерно распределенная нагрузка от собственного веса вспомогательной балки

q = q_n,вб γ_fg= 78,5 · 1,05 = 82,43 кг/м = 0,824 кН/м.

Нормативный изгибающий момент

M_n,max= F_na₁ + q_n,вб l²/8 = 136,89 · 2 + 0,785 · 6² / 8 = 277,31 кН·м.

Расчетный изгибающий момент

M_max= Fa₁ + ql²/8 = 161,78 · 2 + 0,824 · 6² / 8 = 327,27 кН·м.

Максимальная поперечная сила

Q_max = F + ql/2 = 161,78 + 0,824 · 6 / 2 = 164,25 кН.

Проверка несущей способности балки. Проверка прочности по нормальным напряжениям в середине балки:



Резерв несущей способности



Несмотря на большое недонапряжение сечение принято, так как при изменении сечения в меньшую сторону, принимая ближайший профиль I45 сW_x = 1231 см³, перенапряжение составит 5%.

Проверка прочности по касательным напряжениям у опоры:



Проверка прочности на местное напряжение σ_loc в местах приложения к верхнему поясу вспомогательной балки сосредоточенной нагрузки от балок настила (см. рис. 4.1):



где σ_loc = F/(l_eft_w) = 161,78/ (18,94 · 1) = 8,54 кН/см²,

здесь F= 2 ∙ 80,89 = 161,78 кН – расчетное значение сосредоточенной силы, равное двум реакциям от балок настила;

l_ef = b + 2t_f^׳ = 12,5 + 2 · 3,22 = 18,94 см – условная длина распределения сосредоточенной нагрузки на стенку вспомогательной балки;

b = 125 мм – ширина пояса балки настила;

t_f^׳ = t_f+ R= 15,2 + 17 = 32,2 мм – расстояние от наружной грани полки до начала внутреннего закругления стенки.

Общую устойчивость балок настила проверять не надо, поскольку их сжатые пояса надежно закреплены в горизонтальном направлении часто рас- положенными и приваренными к ним балками настила.

Проверка жесткости. Прогибы, определяемые от нормативных нагрузок, не должны превышать их предельных значений, установленных нормами проектирования. Для однопролетной балки, нагруженной сосредоточенной нагрузкой, проверка прогиба производится по формуле



где M_n,max– максимальный момент в балке от нормативной нагрузки;

f_u = l/250 = 2,4 см при пролете l= 6 м (см. табл. 4.1).

Принятое сечение удовлетворяет условиям прочности и жесткости.

В случае невыполнения любого из условий необходимо изменить сечение, приняв по сортаменту следующий номер двутавра и вновь проверить прочность и жесткость балки.

Определяем вес вспомогательной балки на 1м² рабочей площадки:

g_n,вб = 78,5/a² =78,5 / 4,5 = 17,44 кг/м² = 0,174 кН/м².

4.5. Выбор оптимального варианта балочной клетки

Необходимо сравнить два варианта балочных клеток. Сравнение производится по расходу материала, а также по количеству балок, определяющему трудоемкость монтажа и стоимость их перевозки. результаты которого заносятся в табл. 4.5. В качестве определяющего показателя при выборе оптимального варианта принимается расход стали (кг/м²). В том случае, если расход стали по вариантам отличается менее чем на 5 %, в качестве оптимального варианта принимается вариант с меньшим количеством монтажных элементов. Выявленный на основании сравнения оптимальный вариант принимается к дальнейшей разработке.

Анализируя показатели, представленные в табл. 4.5, можно сделать следующие выводы:

– для балочных клеток с применением стального настила (1-й и 2-й варианты) первый вариант предпочтительнее второго по расходу стали на 1 м² рабочей площадки и по количеству монтажных единиц.

– для балочных клеток с применением железобетонного настила (3-й и

4-й варианты) третий вариант несколько уступает четвертому по расходу железобетона на настил, но значительно выгоднее по расходу стали на 1 м² рабочей площадки и по количеству монтажных единиц.

Таблица 4.5

Сравнение вариантов балочной клетки (расход на 1 м²

рабочей площадки)

Наименование элемента	Расход железобетона, м3/м2	Расход стали, кг/м2	Количество балок, шт.	Расход железо- бетона, м3/м2	Расход стали, кг/м2	Количество балок, шт.
	Настил стальной
	1-й вариант			2-й вариант
Настил	–	62,8	–	–	62,8	–
Балки настила	–	26	62	–	11,4	132
Вспомогательные балки	–	–	–	–	19	26
Суммарный расход стали	–	88,5	–	–	93,2	–
	Настил железобетонный
	3-й вариант			4-й вариант
Настил	0,12	–	–	0,1	–	–
Балки настила	–	19	26	–	15,75	56
Вспомогательные балки	–	–	–	–	17,44	18
Суммарный расход материалов	0,12	19	–	0,1	33,19	–

Принимаем третий вариант балочной клетки:

тип – нормальный;

настил – железобетонный толщиной t_н = 12 см;

балки настила – стальные прокатные с шагом а₁ = 3 м.

Прежде, чем приступить к дальнейшему проектированию элементов балочной площадки, необходимо принятый вариант согласовать с руководителем курсового проектирования.

5. РАСЧЕТ ГЛАВНОЙ БАЛКИ

Применяют сечение главной балки двутавровое симметричное, сваренное из трех металлопрокатных листов, так как прокатные балки из-за ограниченности размеров профиля не могут удовлетворить требования по несущей способности и жесткости (большие пролеты и значительные нагрузки на балку).

5.1. Определение усилий

Расчетная схема однопролетной балки с шарнирным опиранием на колонны представлена на рис. 5.1.

Пролет главной балки lравен наибольшему расстоянию между колоннамиL. Расстояние между главными балками b равно шагу колонн В.



Рис. 5.1. Расчетная схема главной балки

При частом расположении балок настила (а₁ = 3 м) < (l/5 = 18/5 = 3,6 м) сосредоточенную нагрузку, передаваемую на главную балку от балок настила, заменяют равномерно распределенной нагрузкой, собираемой с соответствующей грузовой площади, так как ломаная эпюра изгибающего момента от сосредоточенных сил близка к кривой (см. рис. 4.10).

Нормативная нагрузка



Расчетная нагрузка



Расчетный изгибающий момент в середине пролета



Нормативный изгибающий момент

_{Mn,max = αqnl}²_{/8 = 1,04 · 94,44 · 18}² _{/ 8 = 3977,81 кН∙м.}

Расчетная поперечная сила в опорном сечении



где = 1,04 – коэффициент, учитывающий собственный вес главной балки (предварительно принимается  = 1,02 – 1,05).

5.2. Компоновка сечения

Компоновка сечения, т.е. определение размеров элементов в пределах принятого типа сечения (рис. 5.2), является технико-экономической задачей: необходимо выбрать размеры элементов сечения из предлагаемого перечня (сортамента) таким образом, чтобы удовлетворялись условия прочности, жесткости, общей и местной устойчивости, конструктивные требования при минимальном весе конструкции. Из определяемых параметров сечения балки (h,h_w,t_w,b_fи t_f) наибольшее влияние на вес оказывает высота h.



Рис. 5.2. Сечение главной балки и эпюры распределения

напряжений σ и τ по сечению

В курсовой работе балку рассчитываем в упругой стадии работы, хотя при выполнении определенных условий (см. п. 4) составная сварная балка может рассчитываться с учетом пластических деформаций, при этом расчет на прочность балки переменного сечения следует выполнять только для одного сечения с наиболее неблагоприятным сочетанием усилий M и Q.

В первую очередь необходимо обеспечить прочность балки. Требуемый момент сопротивления балки, определяемый из условия прочности по нормальным напряжениям:

W_n,min = M_max/(R_yγ_c) =469036 / (24 · 1) = 19543,17 см³,

где R_y = 23 кН/см² при толщине проката более 20 мм;

R_y = 24 кН/см² при толщине проката t  20 мм.

Выполняем компоновку сечения балки таким образом, чтобы фактический момент сопротивления принятого сечения был не меньше требуемого (W_x > W_n,min), тем самым обеспечим условие прочности.

Назначаем высоту сечения балки h, которая определяется максимально допустимым прогибом балки, экономическими соображениями и строительными габаритами площадки.

Наименьшая рекомендуемая высота балки h_min определяется жесткостью балки – ее предельным прогибом f_u (второе предельное состояние). Условие жесткости при равномерно распределенной нагрузке по длине балки



где q_n – суммарная погонная нормативная нагрузка на балку.

Из условия жесткости минимальная высота балки



где f_u = 4,5 см – предельный прогиб главной балки пролетом l = 18 м, определенный по табл. 4.1.

Оптимальная высота балки по металлоемкости



где k = 1,2 – 1,15 для сварных балок (меньшее значение принимается для балок переменного сечения по длине);

t_w – толщина стенки балки в см, определяемая по эмпирической зависимости с округлением до стандартной толщины листового проката:

t_w = 7 + 3h/1000 = 7 + 3 · 1500 / 1000 = 11,5 мм. ≈ 12 мм.

Высоту разрезной балки можно принять приблизительно равной h_min (обычно в пределах от 1/10 до 1/13l: при пролете l = 18 м от 1,8 до 1,4 м); принимаем h = 1,5 м.

Соотношение между высотой балки и толщиной стенки оказывает большое влияние на экономичность сечения; при этом, чем относительно тоньше стенка, тем больше высота и выгоднее сечение балки. Рекомендуемые соотношения высоты балки и толщины стенки приведены в табл. 5.1. Если полученное соотношение h/t_w не укладывается в рекомендуемые пределы, необходимо изменить t_w и вновь вычислить величину h_opt.

Таблица 5.1