ПРОЕКТИРОВАНИЕ РАБОЧЕЙ ПЛОЩАДКИ. Включая сварку проектирование рабочей площадки
 Скачать 3.55 Mb.
|
|
Значения коэффициента ссr в зависимости от значения δ
Проверяем местную устойчивость стенки: σ/cсr = 21,23 / 44,38 = 0,48 < γс = 1. Устойчивость стенки в середине балки обеспечена. Проверка местной устойчивости стенки в отсеке с измененном сечением (рис. 5.9). Расчетное сечение в отсеке располагается на расстоянии hw/2 от правого ребра и х от опоры: х = а1+ а – hw/2 = 1,5 + 3 – 1,5 / 2 = 3,75 м. Расчетные усилия в сечении: М = qx (l – x)/2 = 115,03 · 3,75 (18 – 3,75) / 2 = 3073,46 кН∙м;  Краевое напряжение сжатия в стенке σ = M(hw/h)/W1 = 307346 (150 / 155) /13357 = 22,27 кН/см2. Среднее касательное напряжение в отсеке τ = Q/(hwtw) = 603,91 / (150 ∙ 1,2) = 3,36 кН/см2. Локальное напряжение σloc = 0.  Рис. 5.9. К расчету местной устойчивости стенки балки Критическое нормальное напряжение  где cсr = 31,8 – по табл. 5.6 в зависимости от 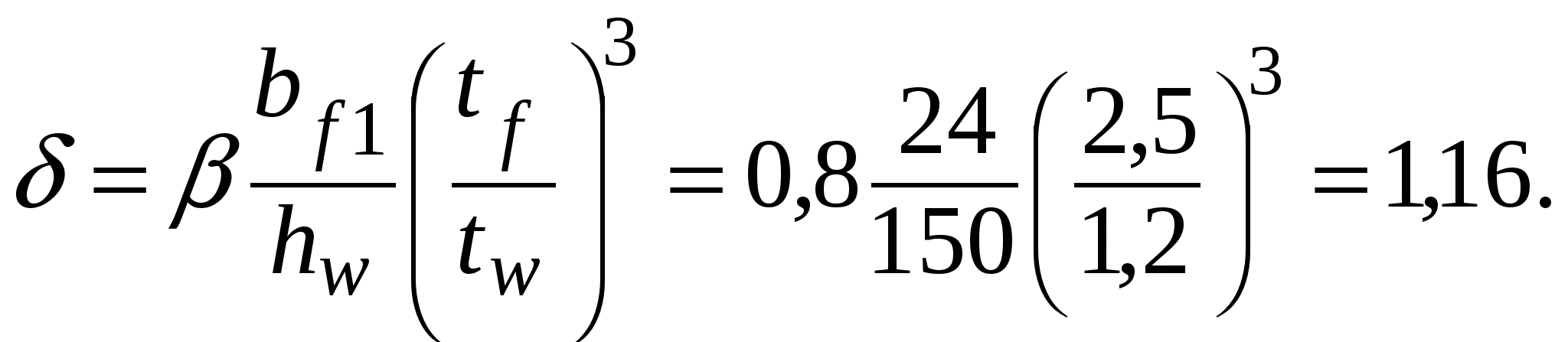 Критическое касательное напряжение 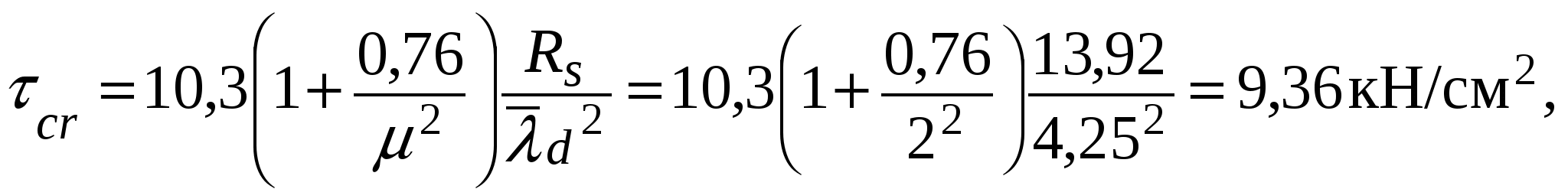 где  – отношение большей стороны отсека a или hw к меньшей d; здесь d = hw = 1,5 м < a = 3 м. Производим проверку:  Стенка устойчива. Проверка местной устойчивости стенки в первом отсеке в сечении на расстоянии от опоры x1 = a1/2 = 1,5 / 2 = 0,75 м (рис. 5.9), здесьa1 = hw. Определяем усилия: M1 = qx1(l – x1)/2 = 115,03 · 0,75 (18 – 0,75) / 2 = 744,1 кН∙м;  Краевое напряжение сжатия в стенке σ = M1(hw/h)/W1 = 74410 (150 / 155) /13357 = 5,39 кН/см2. Среднее касательное напряжение в отсеке τ = Q1/(hwtw) = 949 / (150 ∙ 1,2) = 5,27 кН/см2. Локальное напряжение  Критическое нормальное напряжение  при = 1,16.Критическое касательное напряжение  где  – отношение большей стороны отсека a или hw к меньшей d;здесь d = hw = a1 = 1,5 м – меньшая из сторон отсека. Производим проверку:  Стенка в первом от опоры отсеке устойчива. В случае невыполнения условия устойчивости стенки необходимо увеличить толщину стенки tw или уменьшить расстояние между поперечными ребрами жесткости а и повторно произвести проверку ее устойчивости. 5.6.2. Проверка местной устойчивости стенки балки при наличии местных напряжений (σloc 0) При наличии местных напряжений (только для варианта, в котором имеются местные напряжения) проверку стенки на местную устойчивость следует выполнять в зависимости от значения a/hw, при этом значения M иQ определяют в одном сечении балки. Значения критических напряжений определяются в предположении выпучивания стенки между ребрами жесткости при ее потере устойчивости по одной полуволне при частом расположении ребер (a/hw 0,8) и при более редкой расстановке ребер жесткости (a/hw > 0,8) – по одной или двум полуволнам. Значения нормальных и локальных критических напряжений потери устойчивости при a/hw 0,8 вычисляются: – критическое нормальное напряжение σcr так же, как и при отсутствии местных напряжений по формуле 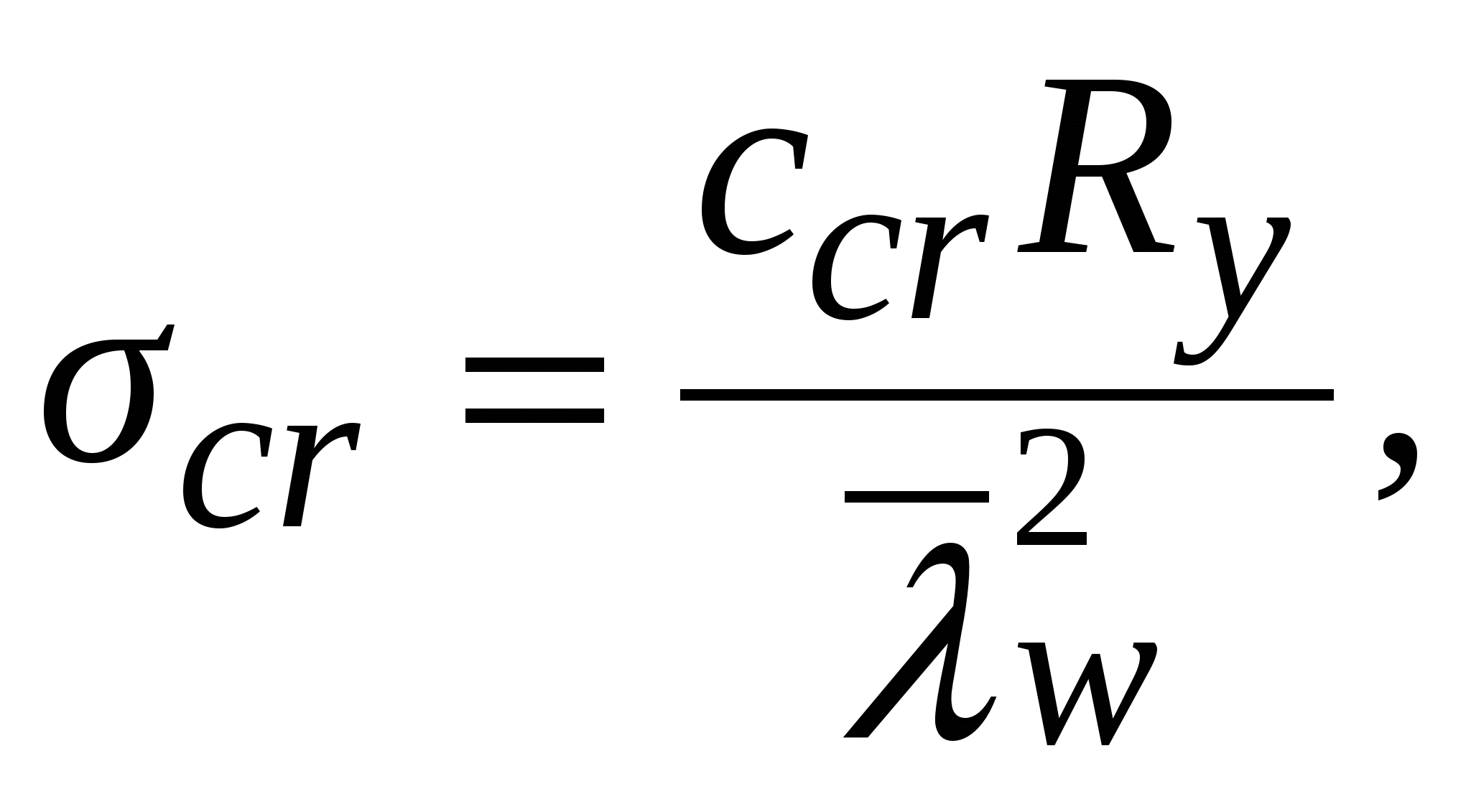 где ccr определяется по табл. 5.6; – критическое локальное напряжение  где с1 – коэффициент, принимаемый по табл. 5.7 в зависимости от a/hw – соотношения сторон проверяемой пластины и значения ρ = 1,04lef /hw – относительной длины загружения пластины местной нагрузкой lef к высоте стенки hw, здесь lef = b + 2tf ; с2 – коэффициент, принимаемый по табл. 5.8 в зависимости от отношенияa/hw и значения δ. Таблица 5.7 Значение коэффициента c1
Таблица 5.8 Значение коэффициента c2
При отношении a/hw> 0,8 рассматривают два случая проверки устойчивости стенки: Первый случай. Вычисляют: – критическое нормальное напряжение σcr по формуле 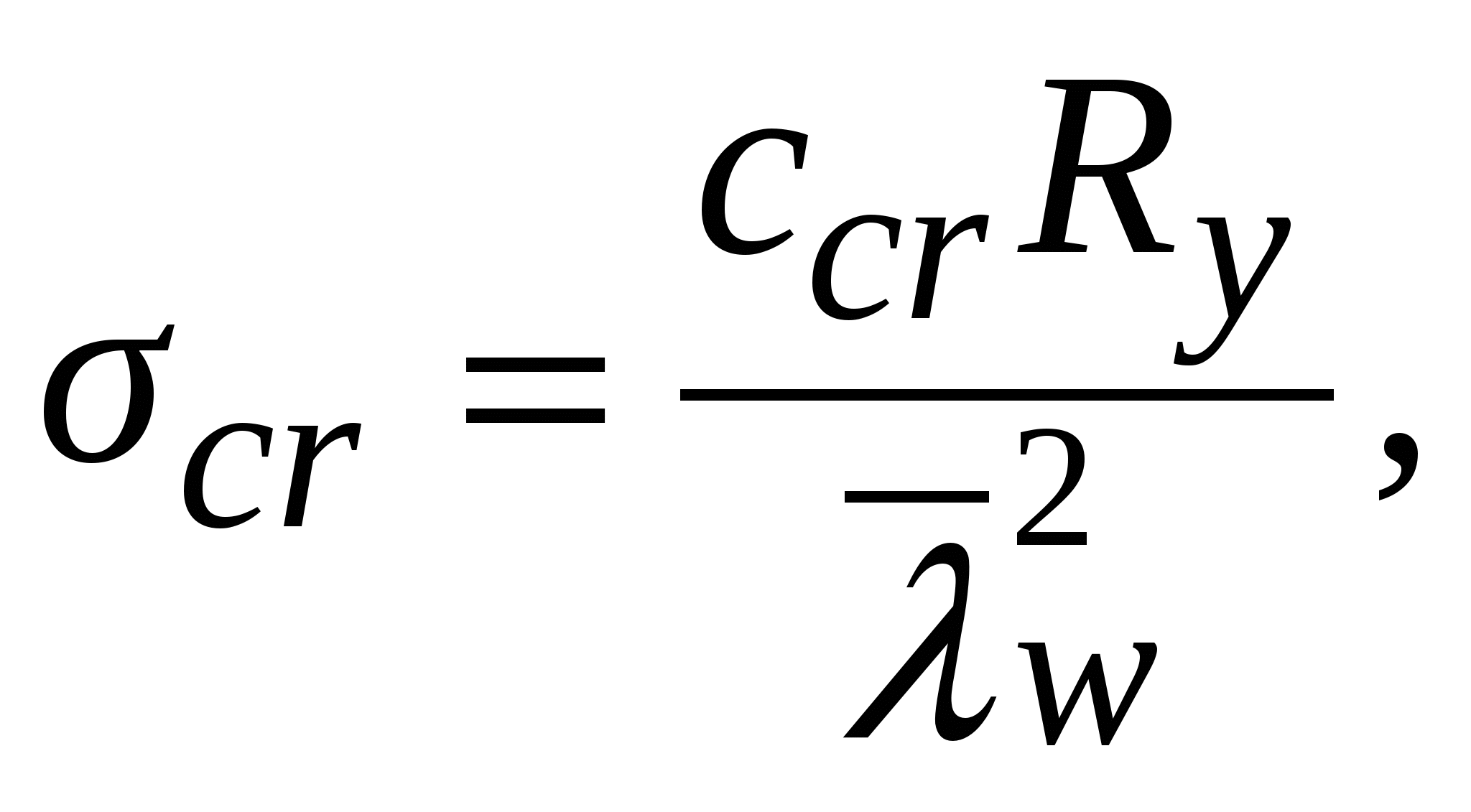 где ccr определяется по табл. 5.6; – критическое локальное напряжение потери устойчивости по формуле  где для его вычисления при определении коэффициентов c1 и c2 по табл. 5.7 и 5.8 вместо a необходимо принять a1 = 0,5aпри0,8 ≤ a/hw ≤ 1,33 и a1 = 0,67hwпри a/hw > 1,33. Второй случай. Вычисляют: – критическое нормальное напряжение σcr по формуле 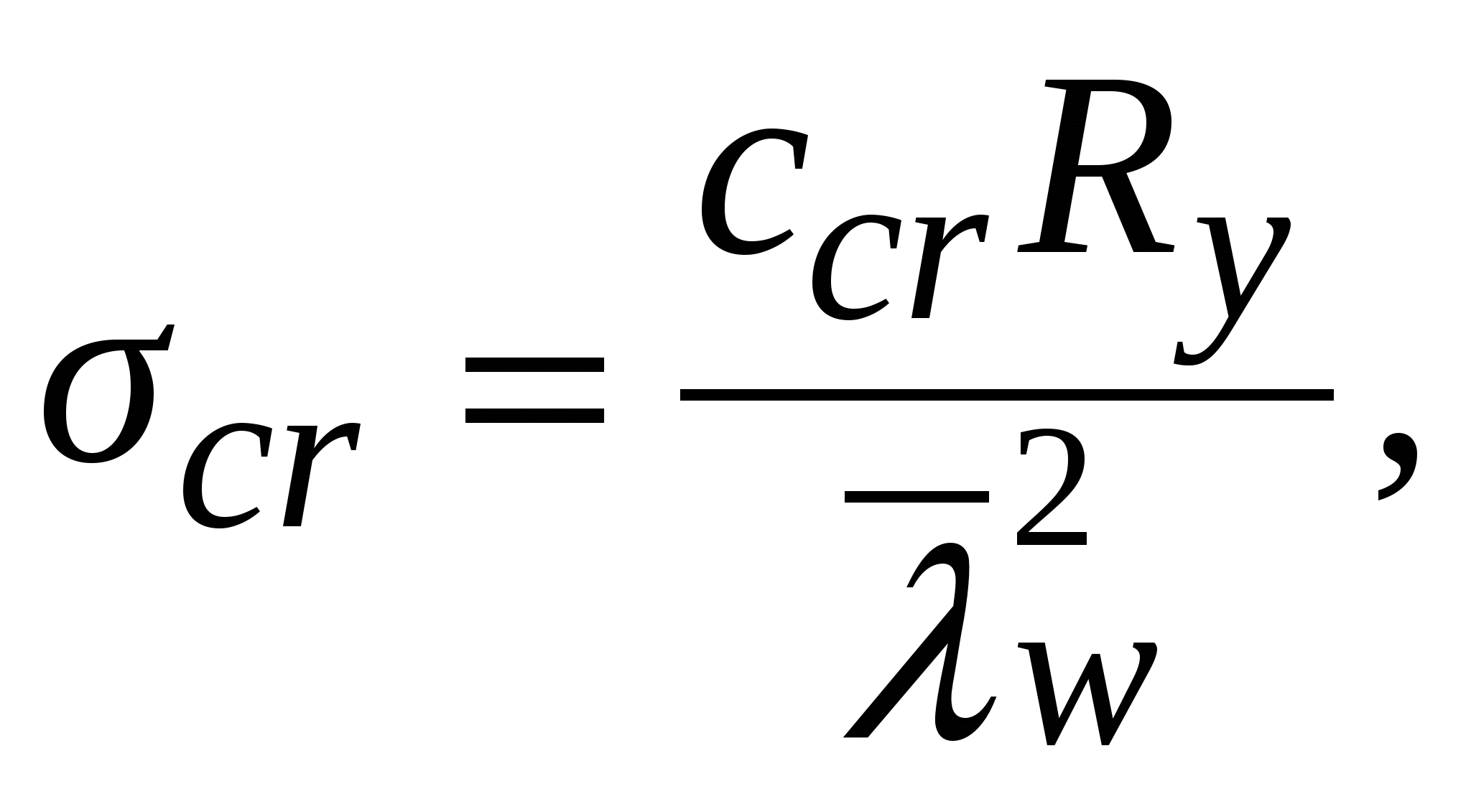где ccr определяется по табл. 5.9; – критическое локальное напряжение потери устойчивости по формуле  где коэффициенты c1 и c2 определяют по фактическому отношению сторонa/hw(если a/hw> 2, в расчете принимаютa/hw = 2). Значения критических касательных напряжений τcr во всех случаях вычисляют по фактическим размерам отсека. Таблица 5.9 Значения коэффициента ccr в зависимости от отношения a/hw
Проверка местной устойчивости стенки при наличии местных напряжений в отсеке с измененном сечением (в качестве примера). Нормальное напряжение в среднем отсеке = 22,27 кН/см2. Среднее касательное напряжение τ = 3,36 кН/см2. Локальное напряжение от сосредоточенной нагрузки на верхнем поясе loc= 13,58 кН/см2. При принятом шаге поперечных ребер жесткости а = 3 м отношение сторон отсекаa1/hw = 300 / 150 =2 > 0,8. следовательно, рассматриваются два случая проверки устойчивости стенки: Первая проверка. Значение критического нормального напряжения  где ccr= 31,8, определенное по табл. 5.6 при δ = 1,16. Значение критического локального напряжения 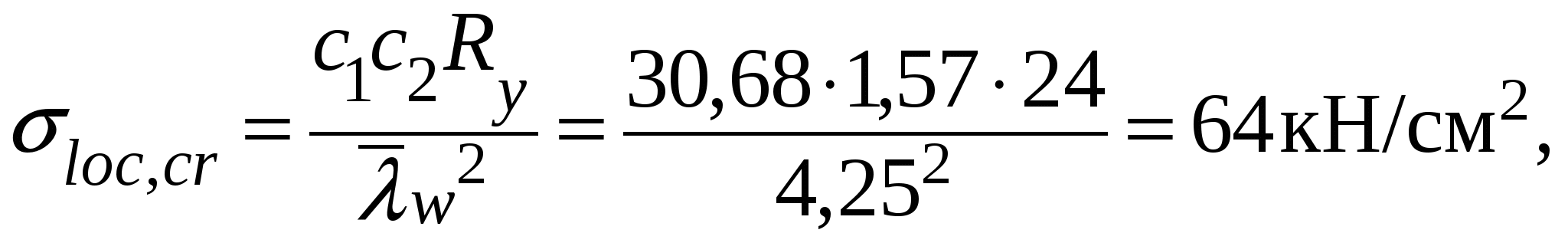 где при вычислении коэффициентов с1 и с2 при a/hw = 2 > 1,33 вместо а при- нимаем а1 = 0,67hw= 0,67 ∙ 150 = 100,5 см, следовательно, a1/hw = 100,5 / 150 = 0,67; ρ = 1,04lef /hw = 1,04 ∙ 20,5 / 150 = 0,14 (здесь lef = b + 2tf = 15,5 + 2∙2,5 = 20,5 см – условная длина распределения напряжений от сосредоточенной нагрузки); с1 = 30,68 – коэффициент, определяемый по табл. 5.7 в зависимости отa1/hw = 0,67 и ρ = 0,14; с2 = 1,57 – коэффициент, определяемый по табл. 5.8 в зависимости отa1/hw = 0,67 и δ = 1,16. Значение критического касательного напряжения τcr = 9,36 кН/см2. Проверяем местную устойчивость стенки:  Вторая проверка. Значение критического нормального напряжения  где ccr= 84,7 – коэффициент, определяемый по табл. 5.9 в зависимости от a/hw = 300 / 150 = 2. Значение критического локального напряжения  где с1 = 12,84 – коэффициент, определяемый по табл. 5.7 в зависимости от a/hw = 2 и ρ = 0,14; с2 = 1,87 – коэффициент, определяемый по табл. 5.8 в зависимости отa/hw = 2 и δ = 2,16. Значение критического касательного напряжения τcr = 9,36 кН/см2. Проверяем местную устойчивость стенки:  Стенка устойчива. Стенки высоких балок (h > 2 м) 1-го класса, у которых при действии нормальных напряжений σ от изгиба устойчивость не обеспечена, а также при значениях условной гибкости  (где σ – напряжение в сжатом поясе балки), для обеспечения их устойчивости следует укреплять продольным ребром жесткости, устанавливаемым дополнительно к поперечным ребрам. Продольные ребра располагаются на расстоянии (0,2 – 0,3)hw от границы сжатого отсека. Их наличие разбивает стенку по высоте на верхний и нижний отсеки, устойчивость которых рассчитывается порознь по СП [4].Пластинку верхнего отсека при необходимости можно укреплять дополнительными короткими ребрами жесткости, доводя их до продольного ребра. 5.7. Проверка жесткости главной балки При равномерно распределенной нагрузке на балку проверка производиться по формуле 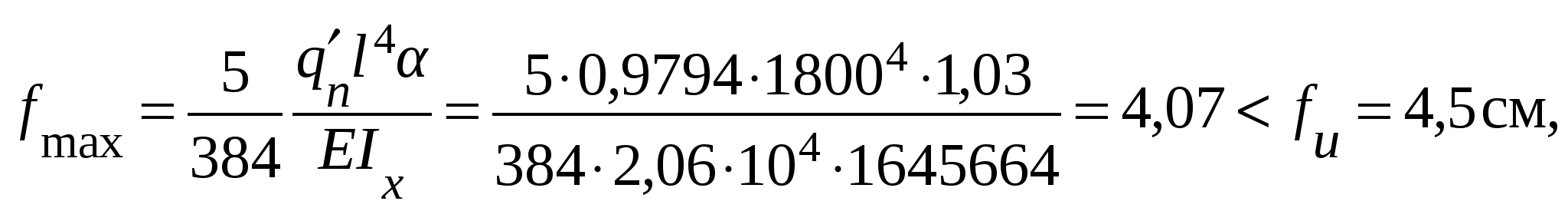 где α = 1,03 – коэффициент, учитывающий увеличение прогиба балки за счет уменьшения ее жесткости у опор, вызванного изменением сечения балки по длине. Расчеты показали, что принятое сечение главной балки удовлетворяет эксплуатационным требованиям, при этом балка в целом и ее элементы по всем предельным состояниям имеют резерв несущей способности и жесткости. Следовательно, возможна корректировка сечения, например, за счет уменьшения толщины стенкиtw до 10 мм. Произведем для примера проверку сечения балки с толщиной стенки tw = 10 мм. Проверка прочности по нормальным напряжениям:  момент сопротивления Wx = 2Ix/h = 2 · 1589414 / 155 = 20509 см3; момент инерции Ix = Iw + 2If = twhw3/12 + 2bftf(hf/2)2 = 1 · 1503/12 + 2 · 45 · 2,5 (152,5 / 2)2 = = 1589414 см4. Проверка прочности балки в опорном сечении на срез по касательным напряжениям: 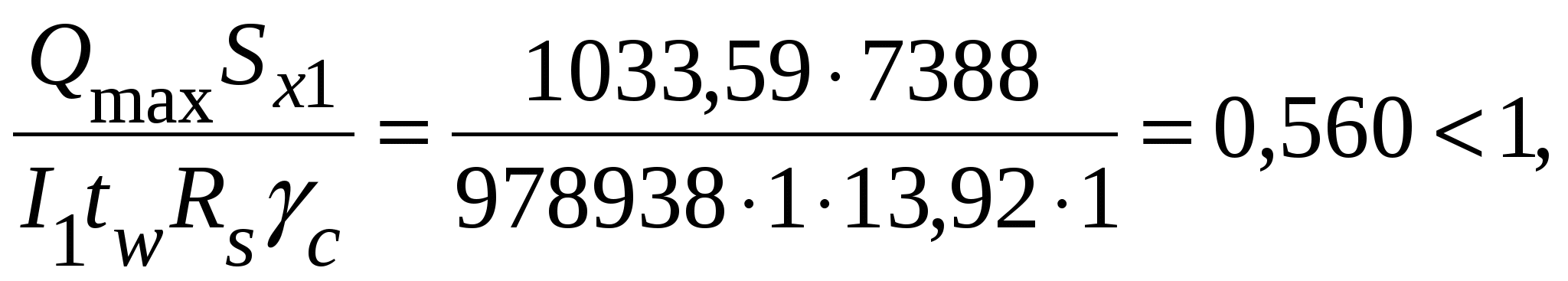 где статический момент половины сечения относительно нейтральной оси   момент инерции I1 = Iw + 2If1 = twhw3/12 + 2bf1tf (hf/2)2 = 1 · 1503/12 + 2 · 24 · 2,5 (152,5 / 2)2 = = 978938 см4. Проверка прочности стенки на местные сминающие напряжения: 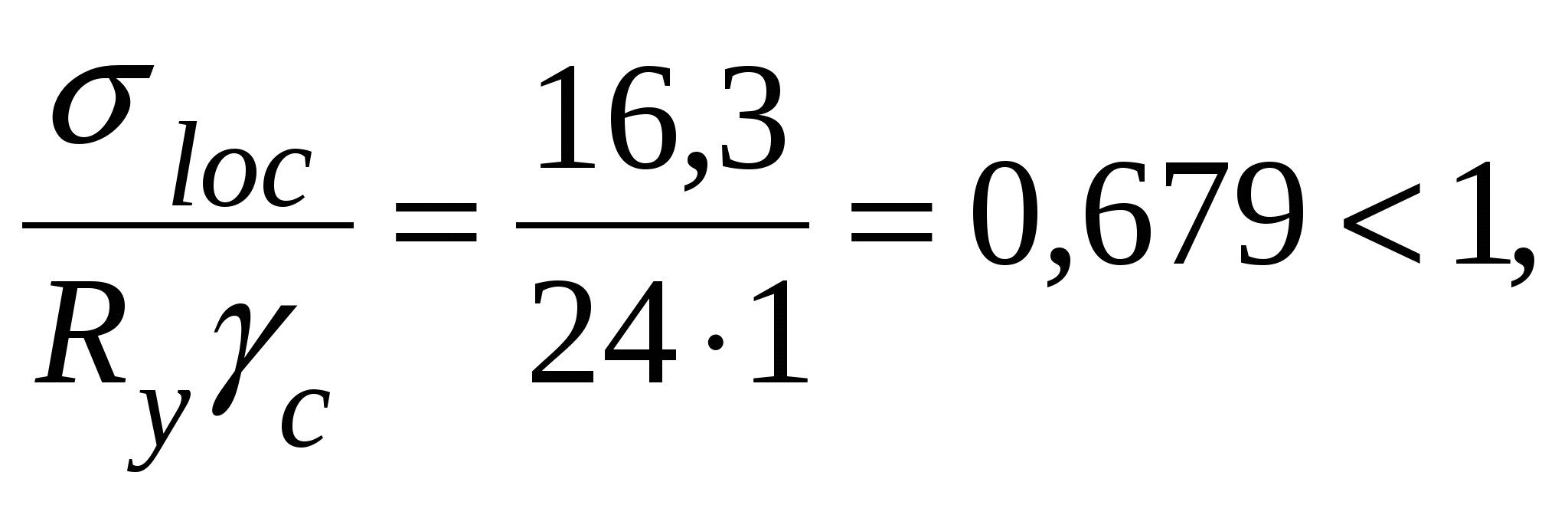 где σloc = F/(leftw) = 334,08 / (20,5 · 1) = 16,3 кН/см2. Проверка местной устойчивости стенки балки. Условная гибкость стенки  следовательно, укрепление ее продольным ребром жесткости не требуется. Краевое напряжение сжатия в стенке σ = M(hw/h)/W1 = 307346 (150 / 155) /13357 = 22,27 кН/см2. Среднее касательное напряжение в отсеке τ = Q/(hwtw) = 603,91 / (150 ∙ 1) = 4,03 кН/см2. Локальное напряжение σloc = 0. Критическое нормальное напряжение  где cсr = 33,3 – по табл. 5.6 в зависимости от 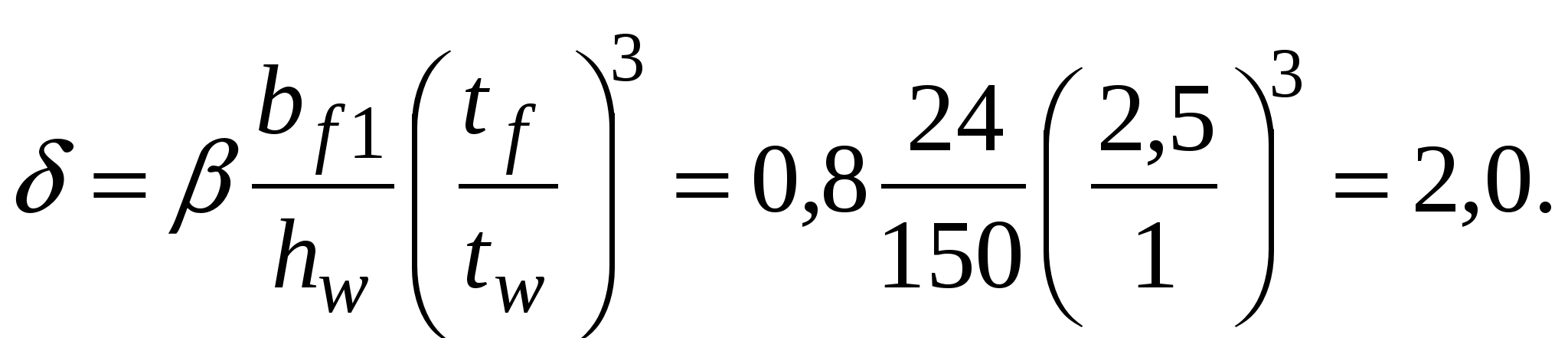 Критическое касательное напряжение 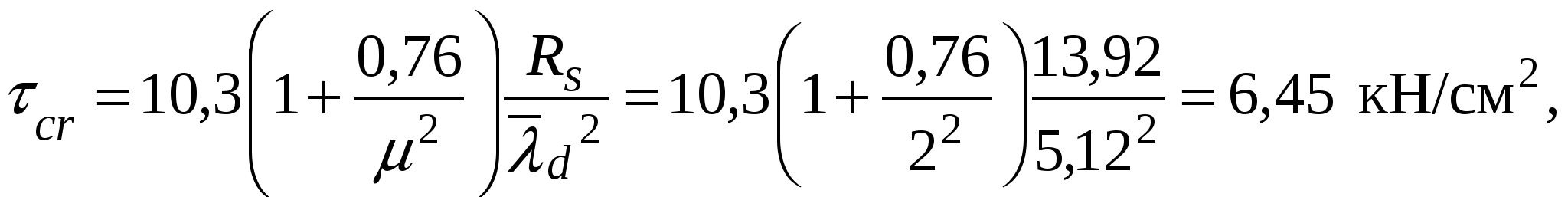 где  Производим проверку:  Проверка жесткости главной балки: 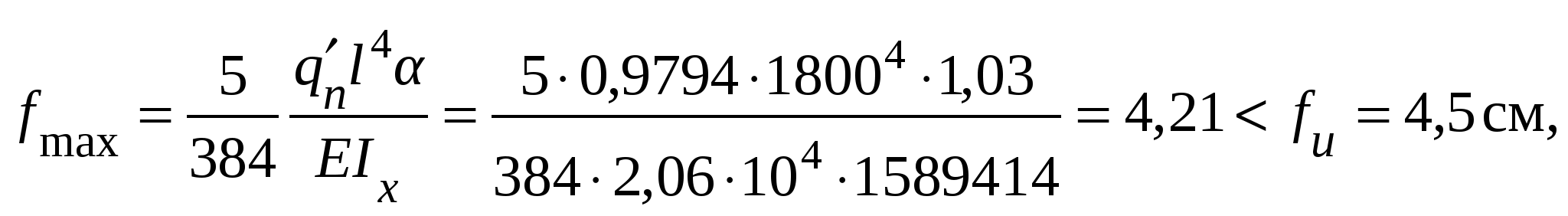 Сечение балки отвечает всем условиям предельных состояний. 5.8. Расчет соединения поясов балки со стенкой Соединение поясов со стенкой в составной сварной балке осуществляется швами, обеспечивающими совместную работу поясов и стенки и предотвращающими при изгибе балки их взаимный сдвиг. При наличии местной нагрузки, действующей на пояс от балок настила в месте, не укрепленном поперечным ребром жесткости, кроме работы на сдвиг поясные швы испытывают дополнительно срез от местного вертикального давления (рис. 5.10). Соединение выполняется автоматической сваркой угловыми непрерывными швами одинаковой толщины по всей длине балки. Расчет сварного шва производится на прочность по металлу шва или по металлу границы сплавления на усилие, приходящееся на 1 см длины балки. Длина шва соответственно принимается в расчете равной 1 см.  Рис. 5.10. К расчету поясных соединений При βzRwz = 1,15 · 16,65 = 19,15 кН/см2 < βfRwf = 1,1 · 18 = 19,8 кН/см2 шов рассчитываем по металлу границы сплавления по формуле:  где  – усилие на единицу длины шва от поперечной силы на опореQmax, сдвигающее пояс относительно стенки;Sf1 = 4575 см3, I1 =1035188 см4 – статический момент пояса и момент инерции относительно нейтральной оси сечения балки на опоре (см п. 5.4);  – давление от сосредоточенной силы Fb на единицу длины шва; – при расчете по металлу шва (см. табл. 3.6);βz = 1,15 – при расчете по металлу границы сплавления; – расчетное сопротивление сварного соединения при расчете по границе сплавления; Rwf = 18 кН/см2 – расчетное сопротивление сварного соединения при расчете по металлу шва, принимаемое по табл. 2.7 в зависимости от марки сварочной проволоки, которую выбирают по табл. 2.5 для автоматической сварки стали принятого класса; Rwz = 0,45Run = 0,45 · 37 = 16,65 кН/см2 – расчетное сопротивление сварного соединения при расчете по границе сплавления; Run = 37 кН/см2 – нормативное сопротивление основного металла, принимаемое по табл. 2.3. Следует иметь в виду, что TиV вычисляются в одном и том же сечении, т.е. там, где σloc ≠ 0. Требуемый катет сварного шва определяется по формуле 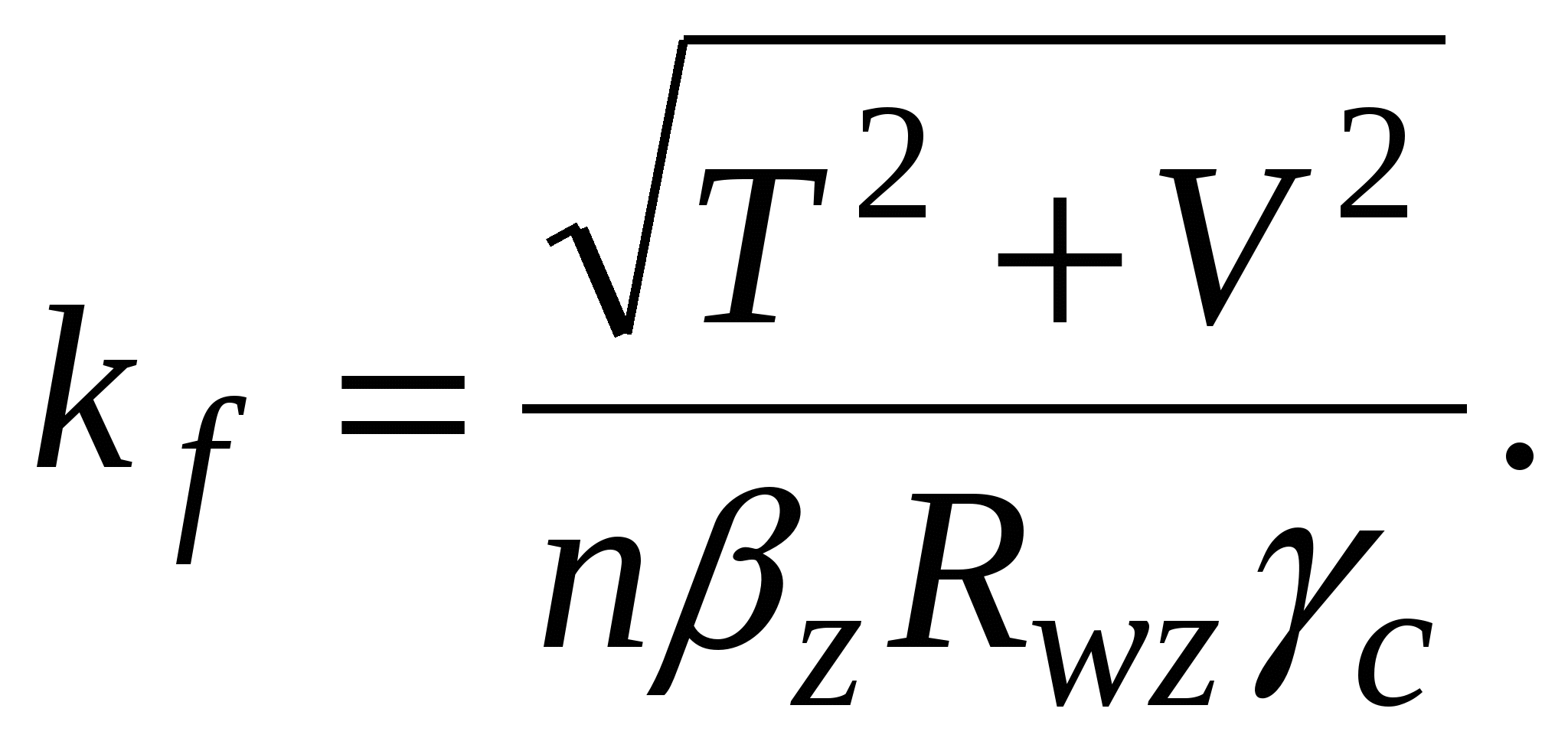 При отсутствии сосредоточенной силы Fb (σloc = 0) второй член под знаком радикала исключается и катет определяется из условия среза шва силой Т: 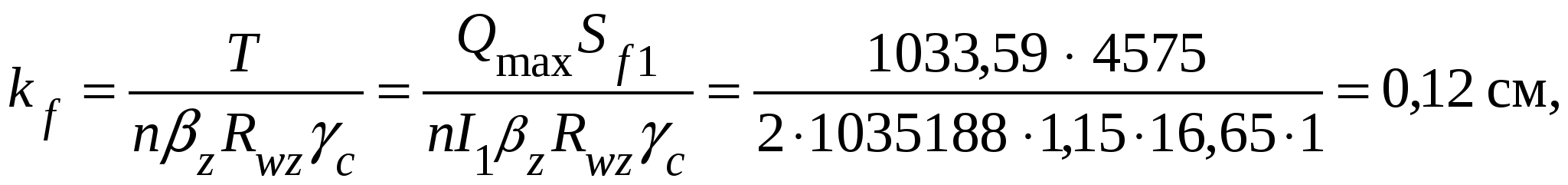 где n = 1 – при одностороннем шве, n = 2 – при двустороннем. По табл. 3.3 для автоматической сварки более толстого из свариваемых элементов tf = 25 мм из стали с пределом текучести до 28,5 кН/см2 принимаем минимальный катет шва kf,min = 5 мм. 5.9. Конструирование и расчет опорной части главной балки Передача нагрузки от главной балки, установленной сверху на колонну, осуществляется через торцевое опорное ребро (возможен вариант передачи опорной реакции балки через ребра, опорная поверхность которых совмещается с осью полки сплошной колонны или ветви сквозной). Торец ребра рассчитывается на смятие, для чего он строгается. Выступающая часть а не должна быть больше 1,5tr (рис. 5.11) и обычно принимается 15 – 20 мм. Расчет ребра производится на усилие Fb, равное опорной реакции балки: Fb = Qmax = 1033,59 кН. Определяем площадь торца ребра: Ar = brtr = F/(Rpγc) = 1033,59 / (36,1 · 1) = 28,63 см2, где Rp = 36,1 кН/см2 – расчетное сопротивление стали смятию торцевой поверхности (см. табл. 2.4). По конструктивным соображениям размеры опорного ребра рекомендуется принимать: tr ≥ 16 мм; bf1 ≥ br ≥ 180 мм.  Рис. 5.11. К расчету опорной части балки Задавшись толщиной опорного ребра tr = 16 мм, определяем его ширину: br = Ar/tr = 28,63 / 1,6 = 17,89 см. Принимаем ребро из листа 20016 мм с площадью Ar = 32 см2. Из условия обеспечения местной устойчивости толщина опорного ребра tr должна быть не менее  где br,ef = (br – tw)/2 = (20 – 1,2) / 2 = 9,4 см – ширина выступающей части опорного ребра.Опорный участок балки следует рассчитывать на устойчивость из плоскости балки (относительно оси z-z) как центрально-сжатую стойку, нагруженную опорной реакцией, с расчетной длиной, равной высоте стенки 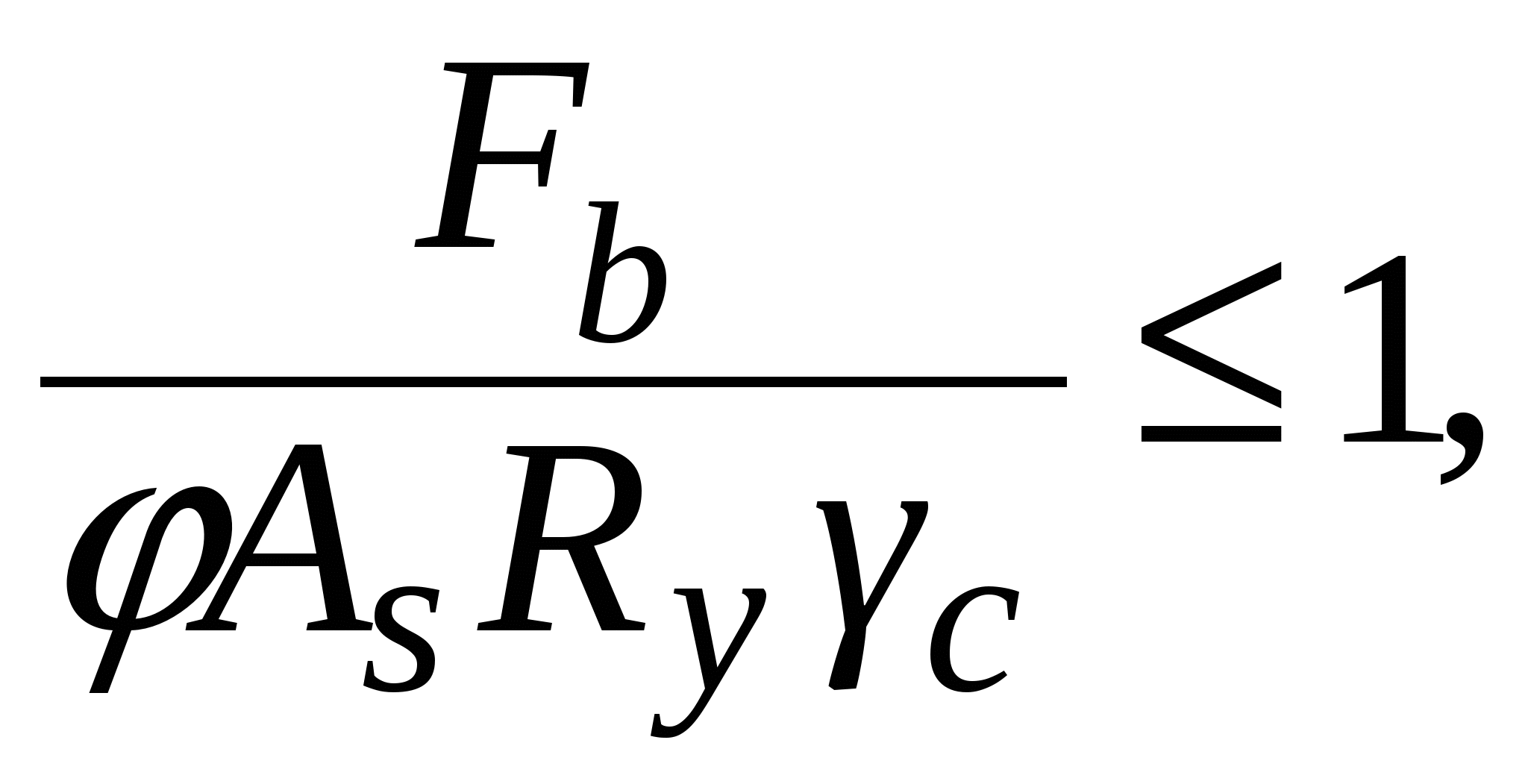 , по формуле где φ – коэффициент устойчивости при центральном сжатии принимаемый в зависимости от условной гибкости  по табл. 6.1 для типа кривой устой-чивости «с»(табл. 5.10). Таблица 5.10 Характеристики кривых устойчивости
Расчетное сечение стержня включает в себя площадь опорного ребра Ar и площадь устойчивого участка стенки, примыкающего к ребру, шириной  Определяем расчетные характеристики стойки: площадь As = Ar + ctw = 32 + 22,85 · 1,2 = 59,42 см2; момент инерции  радиус инерции  гибкость λz = hw/ iz = 150 / 4,24 = 35,38; условная гибкость  Производим проверку:  где φ = 0,878 – коэффициент устойчивости при  = 1,2.Опорная часть балки устойчива. Прикрепление опорного ребра к стенке балки осуществляется механизированной сваркой в среде углекислого газа. Проволока Св-08Г2С по ГОСТ 2246-70* для сварки стали класса С255. Расчетные характеристики сварного шва: Rwf = 21,5 кН/см2; Rwz = 16,65 кН/см2; βf = 0,9; βz = 1,05 (см. табл. 2.5, 2.7 и 3.6). Учитывая, что βzRwz = 1,05 · 16,65 = 17,48 кН/см2 < βfRwf = 0,9 · 21,5 = = 19,35 кН/см2, шов рассчитываем по металлу границы сплавления. Условие прочности сварных угловых швов, работающих на срез: 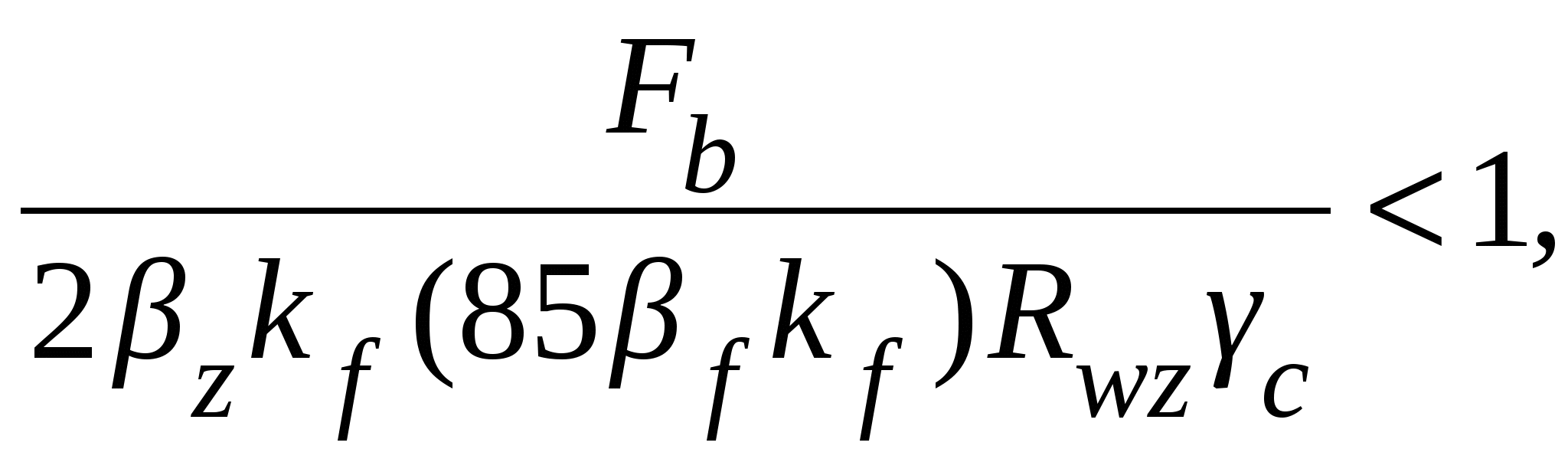 откуда определяем катет шва:  Принимаем шов с kf = 7 мм, что больше kf,min = 4 мм (см. табл. 3.3). Проверяем максимальную длину расчетной части шва:  укладывается в конструктивную длину шва, равную высоте стенки. Ребро привариваем к стенке по всей высоте непрерывными швами. Главные балки скрепляются на опоре между собой через две прокладки суммарной толщиной, равной конструктивному зазору, и с колонной монтажными болтами диаметром 16 – 20 мм, фиксирующими проектное положение балок. Болты взаимного сопряжения балок размещаются в их нижних зонах, что позволяет считать его шарнирным, так как допускается некоторый поворот опорного сечения балок за счет податливости болтового соединения. 5.10. Проектирование монтажного стыка главной балки По условиям перевозки (ограничение массы и габаритов) балка расчленяется по возможности на одинаковые отправочные элементы (марки). В разрезной балке ее элементы (стенка и пояса) стыкуются в одном сечении (универсальный стык). В зависимости от пролета и грузоподъемности транспортных средств главная балка может быть разбита на два или три отправочных элемента (рис. 5.12). Монтажные стыки выполняются сварными или на высокопрочных болтах. В курсовой работе необходимо рассмотреть оба варианта стыка. Чертеж монтажного стыка на болтах можно отобразить только в пояснительной записке. а) б)  Рис. 5.12. Возможное деление главной балки на отправочные элементы При выполнении стыка в середине пролета изгибающий момент максимальный и соответственно максимальные нормальные напряжения σ близки к расчетному сопротивлению основного металла Ry. При расположении стыка в 1/3 пролета (изгибающий момент Mmax к опоре уменьшается) нормальные напряжения σ могут оказаться меньше 0,85Ry. 5.10.1. Монтажный стык на сварке Стык элементов балки осуществляется стыковыми швами (рис. 5.13). Расчетные сопротивления сварных соединений для любого вида сварки принимаются (см. табл. 2.6): при сжатии соединения независимо от методов контроля качества швов Rwy = Ry; при растяжении и изгибе с физическим контролем качества швов Rwy= Ry и Rwy = 0,85Ry, если физические методы контроля не используются. На монтаже применение физических способов контроля затруднено, поэтому расчет растянутого стыкового соединения производится по его пониженному расчетному сопротивлению. Сжатый верхний пояс и стенка соединяются прямым швом, растянутый пояс – косым швом для увеличения длины шва, так как действительное напряжение в поясе σпревышает Rwy. Для обеспечения равнопрочности сварного стыка и основного сечения нижнего пояса достаточен его скос с наклоном реза 2:1. Монтажный стык выполняется ручной сваркой, материалы для сварки выбираются по табл. 2.5. Для сварки монтажного стыка применяют электроды с индексом А (Э42А), обеспечивающие повышенную пластичность наплавленного металла.  Рис. 5.13. Монтажный стык главной балки на сварке Для обеспечения качественного соединения при ручной сварке элементов толщиной более 8 – 10 мм производится V-образная разделка кромок, начало и конец шва выводятся на специальные технологические планки. Для уменьшения сварочных напряжений соблюдается определенный порядок сварки (на рис. 5.13 показан цифрами): сначала сваривают поперечные стыковые швы стенки 1, поясов 2 и 3, имеющие наибольшую поперечную усадку, последними заваривают угловые швы 4 и 5, имеющие небольшую продольную усадку. Оставленные незаверенными на заводе участки поясных швов длиной около 500 мм дают возможность поясным листам несколько вытянуться при усадке швов 2 и 3. Это также позволяет при монтаже совместить торцы свариваемых элементов отправочных марок, имеющих отклонение размеров в пределах технологических допусков. 5.10.2. Монтажный стык на высокопрочных болтах Монтажные стыки на высокопрочных болтах выполняются с накладками (по три на каждом поясе и по две на стенке (рис. 5.14). Усилие с одного элемента на другой передается за счет сил трения, возникающих между соприкасающимися плоскостями, стянутыми высокопрочными болтами. Площади сечения накладок должны быть не меньше площади сечения перекрываемого ими элемента. Наиболее применяемые в конструкциях средней мощности диаметры высокопрочных болтов и их площади сечения приведены в табл. 5.11.  Рис. 5.14. Монтажный стык главной балки на высокопрочных болтах Таблица 5.11 Площади сечения болтов
П р и м е ч а н и е. Размеры, заключенные в скобках, не рекомендуется применять в конструкциях. Диаметры болтов во фрикционном соединении рекомендуется принимать не менее толщины наиболее толстого из соединяемых элементов. При большом количестве болтов в соединении их диаметр назначают возможно большим. При выполнении стыка на высокопрочных болтах рекомендуется принимать один диаметр болтов для поясов и стенки. Принимаем болты db = 24 мм. Диаметр отверстия d под болт делается на 1 – 4 мм больше db. Назначаем отверстие d = 26 мм. Размещение болтов производится согласно требованиям, приведенным в табл. 3.9. Минимальное расстояние между центрами болтов (шаг болтов) в расчетных соединениях определяется условиями прочности основного металла и принимается в любом направлении равным amin = 2,5d = 2,5 · 26 = 65 мм. Принимаем а = 70 мм. Максимальное расстояние между болтами определяется устойчивостью сжатых частей элементов в промежутках между болтами (в крайних рядах при отсутствии окаймляющих уголков amax ≤ 12tmin = 12 · 10 = 120 мм, где tmin– толщина наиболее тонкого наружного элемента) и обеспечением плотности соединения:  Минимальное расстояние от центра болта до края элемента для высокопрочных болтов в любом направлении усилия сmin ≥ 1,3d = 1,3 · 26 = 33,8 мм. Принимаем с = 50 мм. Ширина верхней накладки пояса принимается равной ширине пояса балки bnf =bf = 450 мм. Ширина каждой нижней накладки пояса определяется: b′nf = [bf – (tw + 2kf + 2Δ)] / 2 = [450 – (12 + 2 ∙ 7 + 2 ∙ 10)] / 2 = 202 мм, где Δ = 10 – 15 мм – конструктивный зазор. Толщина каждой накладки пояса tnf= tf /2 + 2 = 25 / 2 + 2 = 14,5 мм. Принимаем верхнюю накладку из листа 45014 мм с площадью сечения Аnf = 63 см2 и две нижних накладки из листа 20014 мм с площадью сечения А′nf = 28 см2. Суммарная площадь накладок Аn = Аnf + 2А′nf = 63 + 2 ∙ 28 = 119 см2 > Аf = 112,5 см2. Горизонтальные болты располагаем в 4 ряда на одной полунакладке. Определяем длину двух вертикальных накладок: lnw = hw– 2(tnf + Δ) = 1500 – 2 (14 + 10) = 1450 мм. Ширина вертикальных накладок bnw = 2а + δ + 4c = 2 · 70 + 10 + 4 · 50 = 350 мм, где δ = 10 мм – зазор между элементами. Толщину каждой вертикальной накладки tnw принимаем равной толщине стенки tw за вычетом 2 – 4 мм, но не менее 6 мм (tnw = 10 мм). Минимальное количество вертикальных рядов принимается равным двум. Расстояния между вертикальными рядами болтов принимаются минимальными, между горизонтальными – близкими к максимальным, количество горизонтальных рядов рекомендуется назначать четным. Максимальное расстояние между крайними горизонтальными рядами болтов (с учетом расстояния до края элемента с = 50 мм) а1= 1450 – 2 ∙ 50 = 1350 мм. Таблица 5.12 Нормативные и расчетные сопротивления высокопрочных болтов из стали 40Х по ГОСТ Р 52643
П р и м е ч а н и е. Размеры, заключенные в скобках, применять не рекомендуется. Стык осуществляем высокопрочными болтами db = 24 мм из стали 40Х «селект», имеющей расчетное сопротивление растяжению высокопрочного болтаRbh = 75,5 кН/см2 (табл. 5.12). Способ регулирования натяжения высокопрочных болтов принимаем по M (моменту закручивания). Расчетное усилие Qbh, которое может быть воспринято каждой поверхностью трения соединяемых элементов, стянутых одним высокопрочным болтом, определяется по формуле  гдеAbn = 3,53 см2 – площадь сечения нетто болта db = 24 мм, принимаемая по табл. 5.11;  – коэффициент трения, принимаемый в зависимости от обработки поверхностей (принят газопламенный способ обработки поверхностей, см. табл. 3.15);γh = 1,12 коэффициент надежности, принимаемый при статической нагрузке и разности номинальных диаметров отверстий и болтов  с использованием регулирования натяжения болтов по М при газопламенном способе обработки поверхностей.Определяем:  Расчет стыков поясов и стенки производим раздельно. Приравнивая кривизну балки в целом 1/ρ = Mmax/(EIx) (здесь – радиус кривизны) к кривизне ее составляющих – стенки Mw/(EIw) и поясов Mf/(EIf), находим изгибающие моменты, приходящиеся на стенку Mw и на пояса Mf, которые распределяются пропорционально их жесткостям, соответственно EIw и ЕIf. Момент инерции стенки Iw = 337500 см4. Момент инерции поясов  Изгибающий момент, приходящийся на стенку Mw = Mmax(Iw/Ix) = 4658,72 (337500 / 1645664) = 955,43 кН∙м. Изгибающий момент, приходящийся на пояса Mf = Mmax(If/Ix) = 4658,72 (1308164 / 1645664) = 3703,29 кН∙м. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
