Внеурочная деятельность младшего школьника Тетрадь Учимся решать логические задачи
 Скачать 1.72 Mb.
|
|
короче зелёного. В задаче продолжается пропедевтическая работа по формированию приёма моделирования. Дети анализируют предметные модели, отражающие данные отношения. 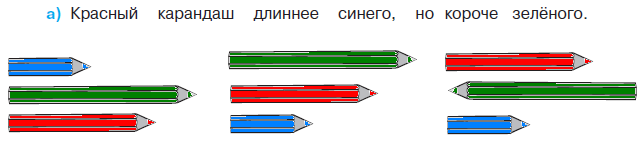 В задании б) возможны различные варианты выполнения. Во второй строке большие мячи не закрашены. В условии ничего не сказано про цвет большого мяча, поэтому дети могут его вовсе не закрашивать или закрасить любым цветом.   Ребята кидали снежки. Андрей (А) бросил дальше, чем Коля (К) и Витя (В), но ближе, чем Серёжа (С). Отметь верный вариант + , а неверный – .Задача направлена на развитие умения моделировать. На её примере можно показать неоднозначность решения (во 2-м случае первым будет Витя, а Коля – вторым).   У 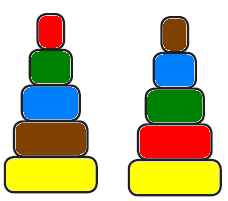пирамидки самое большое кольцо жёлтое. Зелёное кольцо между красным и синим. Синее кольцо рядом с коричневым. Раскрась пирамидку.З  адачу можно решить двумя способами, хотя об этом ничего не говорится в условии. Вариативность решения может стать хорошим материалом для обсуждения. Вполне возможно, что в самостоятельной работе ребята выполнят задание разными способами, включая и неправильные решения. Советуем вынести все полученные решения на доску и выбрать два верных решения. Второй способ решения имеет смысл зарисовать в тетрадь рядом. В новом издании Тетради текст задачи 9 изменён на: У пирамидки зелёное кольцо между красным и синим. Красное кольцо больше синего, но меньше жёлтого. А коричневое кольцо меньше синего. Раскрась пирамидку. Эта задача решается однозначно (см. второй вариант рисунка)  Девочки на праздник завязали банты. У Лены бант не красный, а у Маши самый большой. Какие банты завязали девочки? Соедини имена девочек и их банты.На примере этой задачи дети знакомятся со способом проведения рассуждений на основе установления взаимно однозначного соответствия между данными множествами (множеством девочек и множеством бантов) путем построения графа.  В задании б) на основе анализа текста, аналогичного рассуждениям, приведенным в задаче3, детям предлагается представить результаты умозаключений в виде графа, соединив имена девочек и банты. Задание в) продолжает работу по формированию умения решать логические задачи табличным способом. Главное в этом задании показать динамику заполнения таблицы. Каждый знак + или – является результатом анализа условия или установленных фактов. Рассмотрим пример последовательности заполнения таблицы. Как мы видим, можно сделать не менее 9 выводов.  У Кати бант не жёлтый 1) – . У Лены не красный 2) –. У Маши бант самый большой, значит, жёлтый 3) +, а не синий2) – и не красный 2) –. Следовательно, у Лены не может быть самый большой жёлтый бант 6) –. Если у Лены не красный и не жёлтый бант, значит, он синий 7) +. Тогда у Кати не синий бант 2) –, а красный 9) +. Рассуждения могут быть и более краткими: 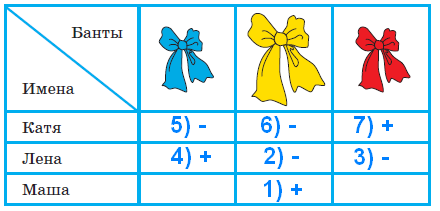 У Маши самый большой бант, значит, это жёлтый бант 1)+. Тогда у Лены бант не жёлтый 2) – . Он и не красный 3) – , значит, он синий 4) +. Следовательно, у Кати не синий 5) – и не жёлтый 6) – , а красный 7) +. В задаче 10 имеется избыточное условие (у Кати не жёлтый бант). Желательно пояснить детям, что это условие – следствие того, что у Маши самый большой бант. Задание г) продолжает работу по установлению истинности и ложности высказываний.   В мешках РИС и САХАР, но надписи ЛОЖНЫЕ. Подпиши, что находится в каждом мешке.Задачи с мешками начинают серию задач с неверными надписями, которые решаются на основе отрицания. Учащиеся знакомятся с различными способами рассуждений. В задаче 11 два рисунка. Задачу на рисунке (1) можно решить 2-мя способами, начиная с анализа надписи любого мешка. Советуем рассмотреть с детьми оба способа рассуждений. 1 способ. Если на первом мешке написано САХАР и надпись неверная, значит, в 1-м мешке РИС, а во втором САХАР. 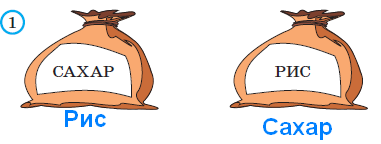 2 способ. Если на втором мешке написано РИС и надпись неверная, значит, в нём САХАР, а в первом мешке РИС. Задача на рисунке 2 отличается решается только одним способом. Советуем начать решение с первой надписи. Дети сами могут сделать следующий вывод: На первом мешке написано МУКА, надпись неверная, значит, в 1-м мешке муки нет, но там может быть и РИС, и САХАР, но что именно – неизвестно. По условию задачи сказано, что в мешках рис и сахар, но надпись МУКА не помогает в дальнейших рассуждениях (не дает возможность сделать вывод и установить новую информацию). На втором мешке написано САХАР, так как надпись ложная, то в мешке сахара нет, значит, там может быть только РИС, тогда в первом мешке САХАР. 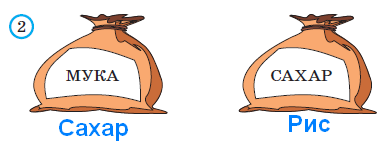 Советуем после решения задачи задать дополнительный вопрос: А могла ли быть во втором мешке МУКА? (Нет.) Почему? (Потому что по условию в мешках РИС или САХАР, муки в мешках не было.)  Рассмотри рисунок. Прочитай предложения в таблице и отметь верные +, ложные -.В Задаче продолжается работа над определением истинности и ложности высказываний. Учащиеся могут испытывать затруднение при анализе первого предложения (На рисунке один лев): считать львёнка львом или нет? Ответ на этот вопрос можно дать, обратившись к имеющимся у детей знаниям из предмета «Окружающий мир». После заполнения таблицы педагог может предложить учащимся составить самостоятельно истинное и ложное предложения по картинке, а затем проанализировать их вместе. 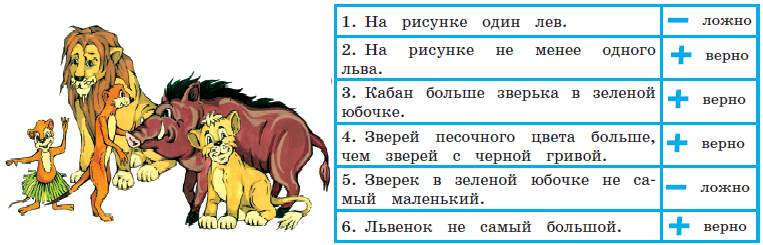  Коля разложил в три коробки синие, красные и зелёные машинки. На первой коробке он написал «синие», на второй – «красные», а на третьей «в первой коробке красные». Какого цвета машинки в каждой коробке, если все надписи неверные?Задача про машинки продолжает серию задач с неверными надписями. Советуем предложить детям решить эту задачу табличным способом. Заполняя таблицу, они ведут рассуждения.  – «На первой коробке написано: СИНИЕ, значит там не синие машинки. Поставим в соответствующую клетку таблицы знак –» и т.д. Рекомендуем ориентировать ребят на запись в клетках таблицы номера последовательности рассуждений рядом со знаком + или – для того, чтобы дети могли прочитать информацию в таблице. Такой совет будет мотивировать учащихся заполнять таблицу более осознанно. Возможны различные варианты, но не любые. Например:  Далее можно предложить классу восстановить цепочку рассуждений по заполненной таблице со знаками и номерами, что полезно не только для умения читать табличные данные, но и для развития умения строить обоснованные рассуждения. Задание в) рассматривается как подведение итогов решения задачи, заменяет ответ. Дети делают выводы по результатам рассуждений, записанных в таблице, и отвечают на вопрос задачи.  На день рождения к Лене пришли четверо друзей: Оля (О), Надя (Н), Петя (П) и Коля (К). Коля пришёл раньше Оли, но не был первым, а Надя пришла последней. Кто пришёл в гости первым? Отметь время прихода каждого гостя на луче точкой («раньше» – точка левее, «позже» – точка правее).Предлагаемая задача относится к задачам на упорядочение множества. В ней рассматривается множество гостей, которое требуется упорядочить с множеством по отношению «прибыть раньше/позже». При выполнении решения задачи 14 учащиеся осваивают приём моделирования. Важно обратить внимание ребят на процесс построения модели. Можно попросить их подписать под точками номера, показывающие последовательность рассуждений. Это поможет детям осознанно построить цепочку рассуждений.  Задание б) призвано подвести итог и сделать вывод.  В мешках МУКА и КРАХМАЛ, но надписи ЛОЖНЫЕ. Подпиши под рисунками, что находится в каждом мешке. К задаче 15 предлагается 2 рисунка, по которым дети будут вести рассуждения. Ситуация на рисунке 1 включает в надпись на мешках отрицание. Анализируя эту надпись, дети знакомятся в неявном виде с законом двойного отрицания: - «На втором мешке написано НЕ МУКА. Мы знаем, что надпись ложная, значит, в этом мешке МУКА, а в первом мешке КРАХМАЛ». 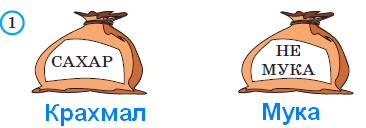 На рисунке одна из надписей не может быть прочитана, что не мешает решить задачу. Хорошо бы после решения задачи подвести учащихся к самостоятельному выводу о том, что для решения этой задачи достаточно одной неверной надписи.  Для установления характера этой надписи советуем продолжить анализ решённой задачи, предложив устно рассмотреть следующую задачу: «В двух мешках СОЛЬ и САХАР, на одном мешке есть надпись, но она ложная. В каких случаях можно узнать, что в каком мешке?» 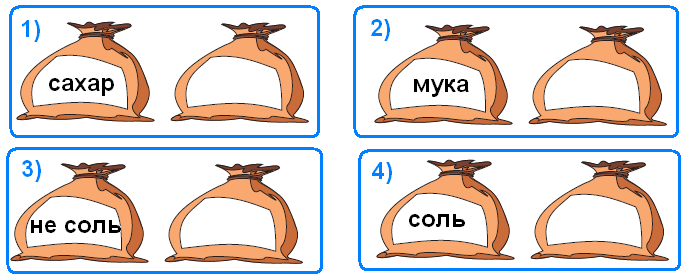 Рассмотрев все случаи, можно сделать выводы, что задача про два мешка решается и с одной надписью, если эта надпись связана с содержимым мешков (как на рисунках 1, 3 и 4) и не решается в других (как во втором случае). Такой анализ позволит познакомить учащихся с обобщённым способом решения аналогичных логических задач.  Рассмотри рисунки. Догадайся, что обозначают знаки + и - в таблице. Заполни таблицу.Аналогичную работу учащиеся выполняли в задаче 12. Однако в данном случае ситуация представлена в более усложнённой форме. Требуется оценить истинность предложений для 4-х рисунков, отличающихся только последовательностью объектов. Задача 16 направлена не только на формирование умения оценивать истинность высказываний, но и развивает пространственные представления младших школьников. Высказывания включают отрицания и кванторы общности, что является новой ступенью в развитии логического мышления. Детям предлагается оценить семь высказываний по 4-м картинкам, что в итоге приводит к составлению 28-ми умозаключений. 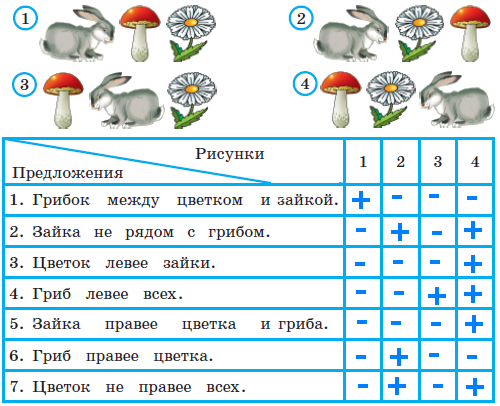  Коля выше Саши, но ниже Юры. Обозначь отрезками рост мальчиков, если:а) отрезок АВ обозначает рост Коли. б) отрезок АВ обозначает рост Юры. в) отрезок АВ обозначает рост Саши. Продолжается работа над формированием у младших школьников приема моделирования. Данный приём рассматривается как способ решения логических задач на упорядочение множества. Ребятам предлагается выполнить рассуждения и достроить три различные модели к одной задаче. Важно ориентировать учащихся на то, что один и тот же отрезок может обозначать любой рост: и маленький, и средний, и большой. Учителю следует иметь в виду: главное не абсолютная длина отрезков, а относительная: отрезок, обозначающий рост более высокого мальчика, должен быть длиннее отрезка, обозначающего рост более низкого. 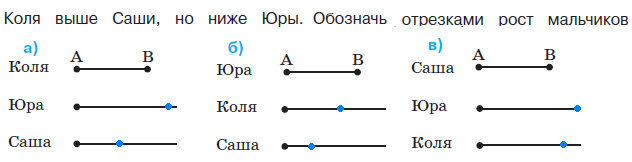 Задания г) и д) направлены на анализ полученных моделей с целью выявления новой информации, вывода.  В мешках ПШЕНО, РИС и ОВЁС, но все надписи неверные. Заполни таблицу. Подпиши под рисунками, что находится в каждом мешке. Задача 18 продолжает формировать табличный способ решения логических задач.  Задание в) позволяет сделать вывод о том, что находится в мешках, и записать ответ.   Петя, Саша и Дима заняли призовые места в эстафете. Дима не был первым, а Петя пришел к финишу не первым и не вторым. Какое место занял каждый из мальчиков? Выполни рассуждения и заполни все клетки таблицы.Заполнение таблицы дети выполняют самостоятельно, а педагог обращается к ним с вопросом: - Какой знак в таблице мог быть поставлен первым? Какой другой вывод можно было сделать из условия задачи? 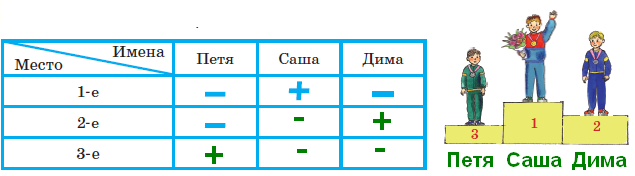  Девочки вырезали снежинки. Оля вырезала снежинок больше, чем Аня, а Катя меньше, чем Оля. Учащимся предлагается выбрать модели, подходящие к заданным в словесной формулировке отношениям. Из шести моделей подходят три. Важно обосновать выбор каждой верной модели, ссылаясь на текст, и указать параметры, по которым не подходят другие модели.  Продолжая работу по выполненному заданию, педагог предлагает классу установить истинность следующих высказываний: Оля вырезала больше всех снежинок. (Истина). Катя вырезала меньше всех снежинок. (Неизвестно) Аня вырезала снежинок больше, чем Катя. (Неизвестно) Аня вырезала снежинок меньше, чем Оля. (Истина) Это поможет ребятам ответить на вопрос: - Почему подходят три различные модели к одному условию?  Задание в) можно выполнить тремя различными способами, которые следует вынести на доску, а в тетрадь записать один из возможных способов.  Второй мешок тяжелее первого, но легче третьего. Какой мешок самый лёгкий? Обозначь массу каждого мешка отрезком. Раскрась мешки. В задаче 21 продолжается работа по обучению решению логических задач на упорядочение множеств с помощью моделей. Если в задаче 17 ребята достраивали модели, в задаче 20 выбирали подходящие по условию модели, то в этом случае дети должны самостоятельно построить модель, отображающую отношения между весом мешков. Учитель может предложить ребятам переформулировать условие, заменив номера мешков на их цвет: «Синий мешок тяжелее красного, но легче жёлтого». 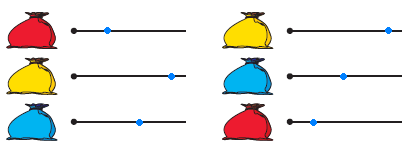 Раскрашивая рисунки в задании в), учащиеся составляют истинные высказывания с противопоставлением (легче, чем…, но тяжелее, чем …); отрицаниями (не тяжелее) и конъюнктивной связью (тяжелее, чем … и чем …). Эту работу удобнее выполнять, опираясь на уже построенные в задании б) модели.  Итак, ученикам предстоит дважды перекодировать информацию: из текстовой формы в так называемую «графическую», а затем в опять текстовую. Завершить выполнение задания целесообразно прочтением вслух полученных высказываний, заменяя картинки указанием цвета мешка. Синий мешок легче жёлтого мешка, но тяжелее красного. Самый лёгкий мешок - красный. Жёлтый мешок тяжелее, чем красный и синий мешки. Синий и красный мешки не тяжелее жёлтого.  У кошки Машки три котёнка: белый, рыжий и разноцветный. Серёжа назвал их Рыжик, Снежок и Букет, но так, что цвет и имя не совпадают. Как зовут котят, если самый светлый из них Букет?В задаче 22 продолжается работу по обучению построению умозаключений по предложенной схеме, делать выводы из данных условий, проверять правильность решения логической задачи табличным способом. Советуем выполнить задания б) и в) одновременно. В этом случае можно подвести ребят к обобщению: таблица заполняется на основе цепочки рассуждений. Последовательность рассуждений может быть различной, но результат, представленный в таблице, однозначен. 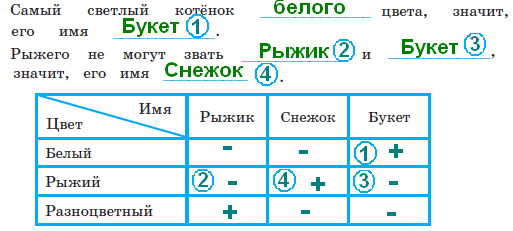 Задание в) помогает ребятам сделать выводы и записать ответ.  Зеленый кубик легче, чем красный, но тяжелее желтого. Обозначь отрезками массу красного и желтого кубиков, если масса зеленого кубика обозначена отрезком АВ. Задача 23 продолжает работу по обучению строить и анализировать модели, делать выводы. Модель, построенная в задании б) с помощью различных отрезков, выступает и как цель деятельности учащихся, и как объект анализа, и как средство наглядности для выполнения следующего задания.  После выполнения задания в) целесообразно прочитать полученные предложения для развития умения строить речевые высказывания и формирования коммуникативных умений младших школьников. 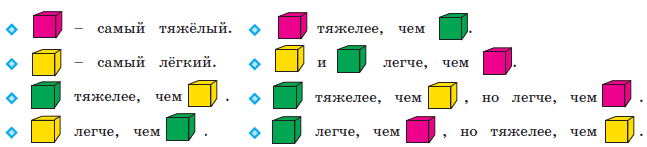 Советуем предложить учащимся найти предложение, которое можно составить неоднозначно: Желтый кубик легче, чем красный (зелёный).   Боре купили игрушку. Если её завести, она прыгает на 3 метра вперёд, а затем на 1 метр назад. Сколько раз ей нужно прыгнуть, чтобы продвинуться на 9 м вперёд? Задача 24 знакомит младших школьников с графическим и табличным способами представления функциональной зависимости, учит делать выводы по табличным данным, оценивать истинность высказываний и их отрицаний. Выполняя задание б), дети учатся создавать графические модели не прямолинейного движения. 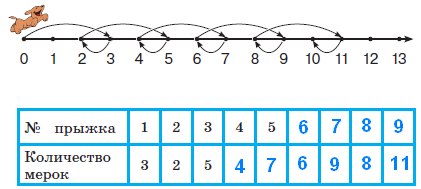 Нумерацию прыжков на схеме можно выполнить заранее (до заполнения таблицы) или непосредственно при заполнении таблицы. При ответе на вопросы г) и д) ребята должны будут обратиться к таблице или схеме. Эти задания направлены на формирование универсальных учебных действий ( умение извлекать информацию из схем и таблиц, т.е. «читать» их). 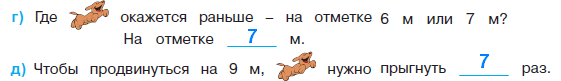  У Вини Пуха три горшочка: с мёдом, джемом и вареньем. На них написано: «МЁД», «ВАРЕНЬЕ», «МЁД или ДЖЕМ». Что находится в каждом горшочке, если все надписи неверные?В задаче 25 продолжается пропедевтическая работа по формированию умения решать логические задачи способом выдвижения и оценки всевозможных гипотез. Заполняя пропуски в высказываниях задания б), дети строят обоснованную цепочку умозаключений.  В задании в) предлагается сделать вывод, перекодировав текстовую информацию в табличный вид.   Аня и Оля подруги. Оля всегда говорит правду, а Аня никогда. Как бы девочки ответили на следующие вопросы? Запиши ответы в таблицу.Задача 26 имеет пропедевтическую направленность. Во многих классических логических задачах требуется придумать вопрос, с помощью ответов на который можно определить требуемую информацию. При решении таких задач важным умением является прогнозирование, так как требуется смоделировать предполагаемую ситуацию и спрогнозировать возможные исходы событий. Задача 26 готовит младших школьников к решению логических задач указанного вида и учит оценивать истинность высказываний и их отрицаний.
|