Внеурочная деятельность младшего школьника Тетрадь Учимся решать логические задачи
 Скачать 1.72 Mb.
|
|
Задание б) призвано обратить внимание детей на тот факт, что есть вопросы, на которые все (и те, кто говорят правду, и те, кто лгут) могут ответить одинаково. Это вопросы 2 и 5. Вопрос 1 может быть отнесен к названной категории вопросов условно, так как Аня, которая по условию задачи лжет, на вопрос: «Как тебя зовут?» может ответить Оля, но не обязательно! Ответом может являться любое имя, кроме Ани.  У Маши три куклы: с рыжими, светлыми и чёрными волосами. Маша назвала их: Белянка, Лисичка и Чернушка, но так, что цвет волос и имя не совпадают. Как зовут каждую куклу, если кукла со светлыми волосами – Чернушка? Задача 27 продолжает работу по формированию умения решать логические задачи на основе построения цепочки умозаключений. В задании б) ученики должны построить следующую цепочку умозаключений: Кукла со светлыми волосами ЧЕРНУШКА, значит, куклу с рыжими волосами не могут звать ЧЕРНУШКА и ЛИСИЧКА, значит, её имя БЕЛЯНКА. Тогда куклу с чёрными волосами зовут ЛИСИЧКА. В задании в) дети должны сделать выводы об, именах кукол, найдя нужную информацию из полученной в задании б) цепочки рассуждений. Задание г) позволяет ребятам провести собственные рассуждения и заполнить таблицу.
 Одна из трёх шоколадных конфет с орешком, поэтому она немного тяжелее других. Взвесили две конфеты. Какая конфета с орешком?Задача 28 направленно на формирование умения решать логические задачи на основе построения цепочки умозаключений, учить анализировать высказывания со связкой «если…, то…» и делать правильные выводы. При выполнении задания б) важно проговорить с детьми полученные высказывания со связкой «если…, то…» 1) Если  , то с орешком  .2) Если  , то с ор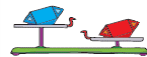ешком  .3) Если  , то с орешком  .Эти задания готовят младших школьников к решению логических задач на взвешивания.  Девочки занимаются танцами, музыкой и рисованием. Оля не рисует, Света не танцует, а Юля любит тишину. Кто чем занимается?В Задаче 29 продолжается формирование умения решать логические задачи на основе построения цепочки умозаключений, анализировать высказывания со связкой «если…, то…» и делать правильные выводы. В задании б) дети должны построить следующую цепочку умозаключений: Если Юля любит тишину, то она не ТАНЦУЕТ и не занимается МУЗЫКОЙ. Значит, Юля РИСУЕТ. Света не РИСУЕТ и не ТАНЦУЕТ. Значит, Света занимается МУЗЫКОЙ. Тогда Оля ТАНЦУЕТ. В задании в) предлагается заполнить таблицу. Важно не забывать, что таблица только способ представления информации, а главное - процесс рассуждения.
Для работы над решённой задачей можно выяснить с ребятами, какое из условий задачи «лишнее» (без каких данных эту задачу можно было бы решить?). Если ребята смогут установить, что информацию о том, что Оля не рисует, можно получить в результате вывода из других данных задачи, значит, работа по решению логических задач не прошла зря!  В одной из трёх коробок конфета, и эта коробка немного тяжелее двух других. Раскрась коробку с конфетой, чтобы получилась верная запись.Задача 30 продолжает работу по формированию умения решать логические задачи на основе построения цепочки умозаключений и анализа высказываний со связкой «если…, то…», а также учит делать правильные выводы. Важно после выполнения задания б) проговорить с ребятами полученные высказывания с импликацией:
 Однажды Ваня и Коля решили уговорить своего деда взять их на рыбалку.– Как же я вас возьму с собой? – отвечает им дед. – Нам нужно будет на другой берег реки переправляться. У меня одна старенькая лодка, которая выдерживает только одного взрослого или двоих детей. Задумались ребята. А Коля вдруг говорит: – Придумал! Есть два способа, как всем переправиться через реку в этой лодке, чтобы лодка у нас осталась! Восстанови идеи Коли. Цель задачи 31 - познакомить младших школьников с логическими задачами на перевозки и табличной формой записи их решения, а также научить строить модель процесса перевозки. Важно обратить внимание на следующие правила заполнения таблицы решения. Решением задач на перевозки является алгоритм. Алгоритмы состоят из действий. В нашем случае действиями являются перевозки, поэтому начинаем запись с указания в центральном столбце переправляющихся, и только после записываем в первом и последнем столбцах тех, кто в момент переправы находится на берегах. Важно помнить, что в одной строке каждый участник переправы записывается только один раз в единственном месте (никто не может в один и тот же момент находится и в лодке, и на берегу). Для проверки правильности записи в столбцах таблицы желательно пересчитывать всех участников переправы в каждой строке. Ошибки оформления, как правило, связаны с тем, что дети забывают кого-то записать или записывают одного и того же героя дважды. Одна из особенностей задач на перевозки состоит в том, что они имеют несколько решений, поэтому мы предлагаем рассмотреть оба варианта решения, сравнить их, найти отличия. В результате выполнения задания б) у ребят в тетрадях должны появиться следующие алгоритмы. 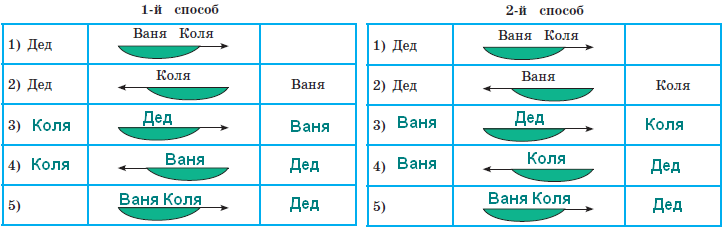  Папа с сыном и дочкой отправились в поход. На их пути встретилась река. У берега плот. Он выдерживает на воде не более одного взрослого или двух детей. Как папе с детьми переправиться на другой берег?Задача 32 аналогична предыдущей, она нацелена на формирование умения решать данные логические задачи (на перевозки) способом перебора и анализа всевозможных действий на каждом этапе. В результате выполнения задания б) должны получиться следующие записи. 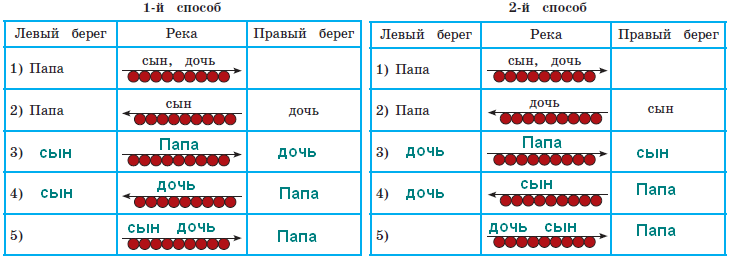  Оля рисовала гуашью трёх цветов: жёлтой, красной, синей, и перепутала все крышки. Какого цвета гуашь в баночках, если на одной из них виден кусочек правильной надписи? Подпиши цвет гуаши в каждой баночке.Задача 33 продолжает работу по формированию умения решать логические задачи на основе построения отрицаний. Можно рассмотреть с ребятами последовательно все баночки с гуашью и сделать выводы, какая краска там может и не может находиться. 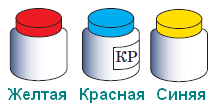 У первой баночки крышка КРАСНАЯ, значит, в ней НЕ КРАСНАЯ краска. В первой баночке может быть или ЖЁЛТАЯ, или СИНЯЯ. У второй баночки крышка СИНЯЯ, значит, там точно не СИНЯЯ краска. На банке видна надпись начинающаяся буквами К и Р… Это может быть только красная краска. Значит, во второй банке КРАСНАЯ краска. У третьей банки жёлтая крышка, значит, там не ЖЁЛТАЯ краска и не КРАСНАЯ (красная уже во второй банке). Получается, что в 3-й баночке СИНЯЯ краска, тогда в первой - ЖЁЛТАЯ краска. Возможны две последовательности установления цвета краски: Во второй банке, затем в первой, а после в третьей Во второй банке, затем в третьей, а потом в первой. Желательно рассмотреть оба варианта на занятии.   Кто живёт в конуре, Тузик или Бобик, если только одна надпись верная?На примере задачи 34 можно познакомить детей с понятием «гипотеза», научить выдвигать и проверять гипотезы, познакомить со способом решения логических задач на основе выдвижения и анализа всевозможных гипотез. При выполнении задания б) дети должны оценить каждую из возможных гипотез. Гипотеза 1. Предположим, что в конуре живет Тузик, тогда надписи  - верная,  - неверная,  - верная.Имеем верных надписей 2, а по условию верных надписей 1. Значит, предположение, что в конуре живет Тузик неверное. Гипотеза 2. Предположим, что в конуре живет Бобик, тогда надписи  - неверная,  - верная,  - неверная.Имеем верных надписей 1, и по условию верных надписей 1. Значит, предположение, что в конуре живет Бобик верное. Ответ. В конуре живет Бобик.  У Лены и Ани фамилии Сидорова и Алимова. У кого какая фамилия, если Лена на 2 года старше Сидоровой?Задача 35 нацелена на формирование умения решать логические задачи способом рассуждения на основе операции отрицания. Дети рассуждают так: - «Если Лена на 2 года старше Сидоровой, значит у Лены фамилия не Сидорова, а Алимова, тогда Сидорова – это фамилия Ани. Если у ребят возникнут трудности в решении, можно будет сделать процесс рассуждения более наглядным. Для этого предлагаем подписать под картинками с изображением девочек их фамилии, рассуждая так: - «Может Лена быть Сидоровой? Нет, так как Лена на 2 года старше Сидоровой. Какая же фамилия может быть у Лены?»  Юра, Коля и Миша играли в машинки. Колина машинка обогнала синюю машинку Юры, но первой была полицейская машинка. Чья машинка выиграла?В Задаче 36 начинается работа по формированию умения решать логические задачи на сопоставление трёх параметров способом построения цепочки умозаключений и табличным способом. В тексте задачи представлена ситуация, в которой необходимо рассмотреть и соотнести три параметра машинок: цвет или предназначение, имя владельца и место машинки в гонках. В задании б) ребятам предлагается восстановить цепочку рассуждений. «Если Колина машинка обогнала синюю машинку Юры, то у Коли не СИНЯЯ машинка, а у Юры СИНЯЯ. Колина машинка обогнала Юрину, но не была первой, значит, она была ВТОРОЙ. А последней пришла СИНЯЯ машинка ЮРЫ». Цепочка рассуждений рассматривает только две машинки: Колину и Юрину. Предполагается, что ребята сами самостоятельно сделают следующие выводы. «Если Колина машинка была второй, а Юрина пришла последней, значит, первой пришла машинка Миши. По условию известно, что первой пришла полицейская машинка, значит, у Миши жёлтая полицейская машинка. У Юры синяя машинка, значит, у Коли красная машинка». Подобные рассуждения ребята должны будут провести при заполнении таблицы в задании в).
Задание г) является подведением итогов решения задачи. Ребята должны проанализировать данные, полученные в таблице, и подвести итог. Полученный результат представляет ответ задачи. Его следует озвучить.  Коля, Боря, Вова и Юра заняли первые четыре места в соревнованиях по лыжам. На вопрос «Кто какое место занял?» Коля ответил: «Я ни первое, ни четвёртое». Боря сказал «Я второе», Вова сказал, что он не последний. Какое место занял каждый мальчик?В Задаче 37 продолжается работа по формированию умения решать логические задачи на сопоставление двух параметров из четырёхэлементных множеств способом построения цепочки умозаключений и табличным способом. В задании б) важно рассмотреть последовательность заполнения таблицы и проговорить всю цепочку умозаключений.
В новом издании Тетради текст задачи 37 изменен на: |
, то конфета в 
.
, конфета в 
, то конфета в 
, то конфета в 
, то конфета в 
.
