Вопрос 1 понятие о статистике как науке термин статистика
 Скачать 323 Kb.
|
|
ВОПРОС 19: ВЫЯВЛЕНИЕ ОСНОВНОЙ ТЕНДЕНЦИИ РАЗВИТИЯ ЯВЛЕНИЯ В РЯДАХ ДИНАМИКИ МЕТОДОМ АНАЛИТИЧЕСКОГО ВЫРАВНИВАНИЯ Тенденция – это общее направление к росту, снижению или стабилизации уровня явления с течением времени. Основная тенденция развития (тренд) представляет собой достаточно плавное и устойчивое изменение уровня явления во времени, более или менее свободное от случайных колебаний. Аналитическое выравнивание ряда динамики используется для того, чтобы дать количественную модель, выражающую основную тенденцию изменения уровней ряда во времени. Оно характеризуется тем, что фактические уровни ряда заменяются расчётными, которые вычислены на основе определённой функции. Расчёт параметров функции производится с помощью метода наименьших квадратов:  . На практике применяется аналитическое выравнивание по прямой, параболе различных порядков, гиперболе. Рассмотрим технику выравнивания ряда динамики по прямой, уравнение которой:  . Для выравнивания по уравнению прямой требованию  удовлетворяет система нормальных уравнений:{   Чтобы определить параметры уравнения а0 и а1 , надо решить данную систему нормальных уравнений. Система уравнений упрощается, если  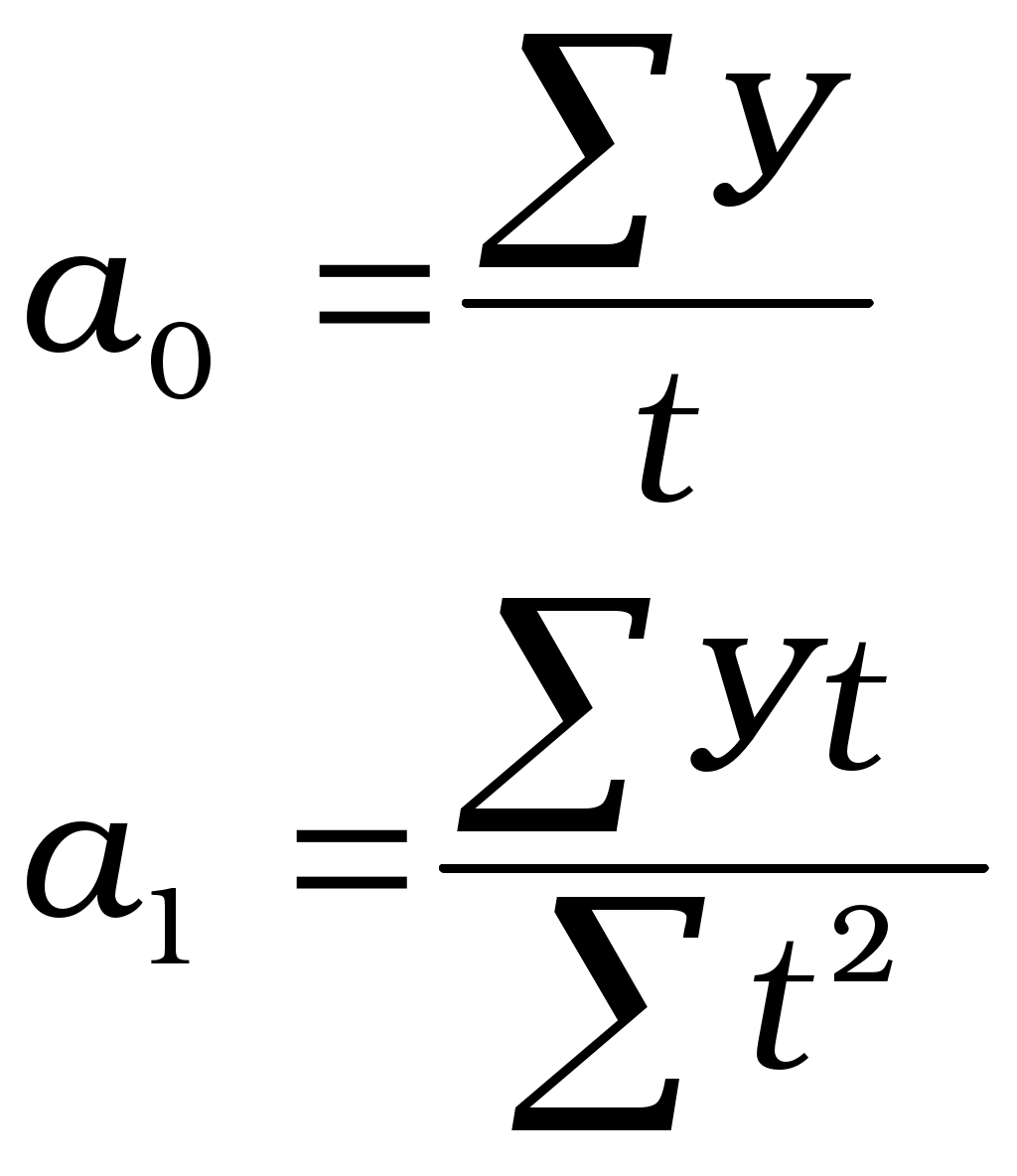. Для этого начало отсчёта времени переносят в середину рассматриваемого периода. Тогда система примет следующий вид: {  Отсюда { Подставляя значения параметров в уравнение прямой, вычисляют расчётные значения уровней ряда динамики  . ВОПРОС 20: РЕГРЕССИОННЫЙ МЕТОД АНАЛИЗА СВЯЗИ Задачи статистики в области изучения взаимосвязей состоят в количественной оценке их наличия, направления и силы связи, в определении формы влияния факторных признаков на результативный. Для решения этих задач применяют методы корреляционного и регрессионного анализа. Корреляция и регрессия тесно связаны между собой: первая оценивает силу (тесноту) статистической связи, а вторая исследует ее форму. Та и другая служат для определения наличия или отсутствия связи между явлениями. Задачи регрессионного анализа: выбор типа модели (формы связи); установление степени влияния независимых переменных на зависимую переменную; определение расчетных значений зависимой переменной (функции регрессии). По форме зависимости различают: линейную регрессию, которая выражается уравнением прямой:  ;нелинейную регрессию, которая выражается уравнениями: параболы:  ;гиперболы:  и т.д.Выбор типа функции может опираться на теоретические знания об изучаемом явлении, опыт предыдущих аналогичных исследований, или осуществляться эмпирически – перебором и оценкой разных типов. Система нормальных уравнений для нахождения параметров линейной парной регрессии имеет следующий вид:  ,где  - усредненное влияние на результативный признак неучтенных факторов; - коэффициент регрессии, показывающий, на сколько изменяется в среднем значение результативного признака при увеличении факторного на единицу собственного измерения.Параметры линейной регрессии можно найти по следующим формулам: 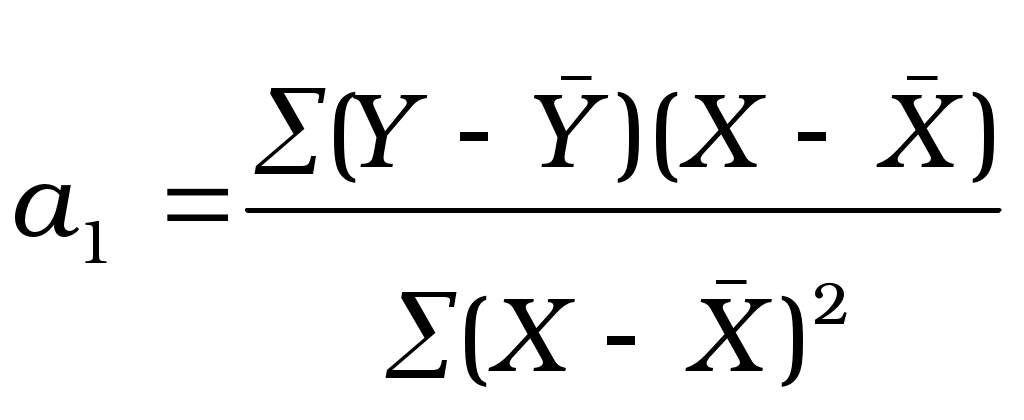  Определив значения a0, a1и подставив их в уравнение связи  , находят значения Yx, зависящие только от заданного значения Х.Таким образом, используя тот или иной тип математического уравнения, можно определить степень зависимости между изучаемыми явлениями, т.е. узнать, на сколько единиц в абсолютном измерении изменяется величина результативного показателя с изменением факторного на единицу. ВОПРОС 21: КОРРЕЛЯЦИОННЫЙ МЕТОД АНАЛИЗА СВЯЗИ Однако регрессионный анализ не дает ответа на вопрос: тесная это связь или нет, решающее воздействие оказывает данный фактор на величину результативного или второстепенный? Для измерения тесноты связи между факторами и результативными показателями используется корреляционный анализ. Слово «корреляция» ввел в статистику английский биолог и статистик Ф. Гальтон в конце XIX в. Корреляционная связь представляет собой частный случай стохастической связи. Наличие этого вида связи присуще многим общественным явлениям. Функция корреляционного анализа сводится к измерению тесноты связи между признаками и оценке факторов, которые оказывают наибольшее влияние на результативный признак. Для определения тесноты связи при линейной форме уравнения применяют линейный коэффициент корреляции, который выглядит следующим образом: 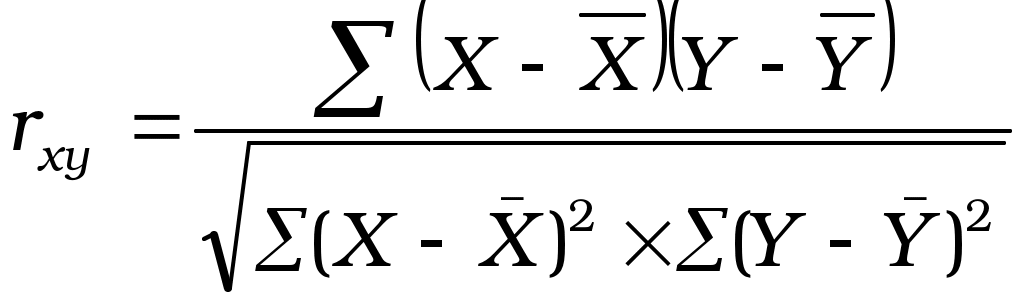 Коэффициент корреляции может принимать значения от –1 до +1, причем, если rxy > 0, то связь прямая, если rxy < 0, то связь обратная, если rxy = 0, то связь отсутствует полностью, а если  , то связь функциональная. Если коэффициент корреляции возвести в квадрат, то получим коэффициент детерминации, который показывает долю вариации результативного признака под влиянием вариации признака – фактора. Для оценки значимости коэффициента корреляции используют t – критерий Стьюдента. При линейной однофакторной связи t – критерий можно рассчитать по формуле:  ,где (n – 2) - число степеней свободы при заданном уровне значимости  и объёме выборки n .Полученное значение tрасч. сравнивают с tтабл., оно должно быть больше, тогда связь существенная, т.е. выбранный фактор влияет на изменение (вариацию) результата. |