Вопрос 1 понятие о статистике как науке термин статистика
 Скачать 323 Kb.
|
|
ВОПРОС 12: ПОНЯТИЕ И ВИДЫ ОТНОСИТЕЛЬНЫХ ВЕЛИЧИН Относительные показатели – это соотношение между количественными характеристиками социально-экономических явлений и процессов. При расчете относительного показателя абсолютный показатель, находящийся в числителе соотношения, называют текущим или сравниваемым, а в знаменателе – основанием или базой сравнения. Относительные показатели могут выражаться в коэффициентах (если база сравнения принимается за единицу); процентах (если база сравнения принимается за 100); промиллях (если база сравнения принимается за 1000); продецимилях (если база сравнения принимается за 10000) или могут быть именованными числами (если получены в результате соотношения разноименных показателей. Например: производительность труда 1 работника). Относительный показатель динамики (ОПД) – отношение уровня исследуемого процесса (явления) в заданный период времени к уровню этого же процесса (явления) в прошлом:  ,где Х0 и Х1 – сравниваемые показатели базисного и отчетного периодов. ОПД показывает во сколько раз отчетный уровень превышает базисный или какую долю составляет. Относительный показатель планового задания (ОППЗ) и относительный показатель выполнения плана (ОПВП) – для исследования перспективного планирования деятельности и сравнения реально достигнутых результатов с ранее намеченными:   Взаимосвязь показателей: ОППЗ × ОПВП = ОПД Относительный показатель структуры (ОПС) – это соотношение структурных частей изучаемого объекта и их целого:  ,где d– доли единицы или удельного веса (%) Сумма всех удельных весов всегда должна быть строго равна 100%. Относительный показатель интенсивности (ОПИ) – характеризует степень распространения изучаемого процесса или явления в присущей ему среде:  ОПСр. – это соотношение одноименных абсолютных показателей, характеризующих разные объекты (предприятия; фирмы; районы; области и т.д.):  .ВОПРОС 13: ПОНЯТИЕ И ВИДЫ СРЕДНИХ ВЕЛИЧИН Наиболее распространённой формой статистических показателей является средняя величина, представляющая собой обобщённую количественную характеристику признака в статистической совокупности. Важнейшее свойство средней величины заключается в том, что она отражает то общее, что присуще всем единицам исследуемой совокупности. В зависимости от характера осредняемых величин используют соответствующие средние величины: среднюю арифметическую, среднюю гармоническую, среднюю геометрическую, среднюю квадратическую, среднюю хронологическую. Средняя величина исчислена как простая и взвешенная. Средняя арифметическая величина исчисляется в том случае, когда общий объём изучаемого признака может быть получен суммирования его индивидуальных значений. Если индивидуальные значения не повторяются, то исчисляют среднюю арифметическую простую величину. Если индивидуальные значения признака часто повторяются, то с помощью группировок образуют ряд распределения и исчисляют среднюю арифметическую взвешенную величину. Во всех случаях средняя арифметическая представляет собой частное от деления общего объёма данного признака в изучаемом явлении на число единиц в совокупности. Средняя арифметическая простая:  .Средняя арифметическая взвешенная:  .Средняя хронологическая рассчитывается в том случае, если имеются данные на определённую дату (обычно на начало месяца, квартала, года). Интервалы между данными должны быть ровными.  ВОПРОС 14: ПОНЯТИЕ ВАРИАЦИИ И СПОСОБЫ ИХ РАСЧЁТА Вариация представляет собой различия в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. Причиной вариации являются разные условия существования разных единиц совокупности. Для того чтобы управлять вариацией и изучать её, разработаны специальные методы исследования – система показателей. К показателям вариации относятся: дисперсия; среднее квадратическое отклонение; коэффициент вариации. С их помощью вариация измеряется, характеризуются её свойства. Дисперсия – это средний квадрат отклонения индивидуальных значений признака от средней арифметической. Для несгруппированных данных:  для сгруппированных данных:  Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и показывает, насколько в среднем отклоняются конкретные варианты от их среднего значения:  .Среднее квадратическое отклонение является абсолютной мерой колеблемости признака и выражается в тех же единицах, что и варианты, поэтому хорошо интерпретируется. Коэффициент вариации представляет собой выраженное в процентах отношение среднего квадратического отклонения к средней арифметической:  Коэффициент вариации используют не только для сравнительной оценки единиц совокупности, но и для характеристики однородности совокупности. Совокупность считается количественно однородной, если коэффициент вариации не превышает 30 %. ВОПРОС 15: ПОНЯТИЕ И КЛАССИФИКАЦИЯ ИНДЕКСОВ Слово «индекс» (index) в переводе с латинского буквально означает указатель, показатель. Индексом называют относительный показатель, характеризующий изменение величины какого-либо явления во времени, пространстве или по сравнению с любым эталоном, планом, прогнозом, нормативами. Основным элементом индексного отношения является индексируемая величина, которая представляет собой значение признака статистической совокупности, изменение которой является объектом изучения. Период, который сопоставляется, называется отчётным. Период, с которым сопоставляют, называют базисным. Индексы классифицируются по следующим признакам: по степени охвата единиц совокупности; по методам расчёта общих индексов; по содержанию изучаемых величин; по базе сравнения. По степени охвата единиц совокупности индексы делятся на индивидуальные и общие. Индивидуальные индексы выражают соотношение отдельных элементов сложного явления, обозначаются буквой iи снабжаются подстрочным знаком индексируемой величины. Например:  Общие индексы показывают изменение всех несопоставимых элементов сложного явления, обозначаются буквой Iи также сопровождаются подстрочным знаком индексируемой величины. По методам расчёта общих индексов различают индексы агрегатные и средние. Агрегатный индекс является основной и наиболее распространённой формой индекса. Его числитель и знаменатель представляют собой набор непосредственно несоизмеримых и не поддающихся суммированию элементов. Средние индексы делятся на средние арифметические и средние гармонические. По содержанию изучаемых величин индексы делятся на индексы количественных и индексы качественных показателей. Индексируемые величины индексов количественных показателей характеризуют общий размер (объём) явления. Индексируемые величины индексов качественных показателей характеризуют уровень явления в расчёте на ту или иную единицу совокупности. В зависимости от базы сравнения индексы бывают базисными и цепными. В системе базисных индексов уровни индексируемого показателя сравнивают с уровнем базисного периода. Например:  и т. д. В системе цепных индексов уровни индексируемого показателя сравнивают с уровнем предыдущего периода. Например:  и т. д. ВОПРОС 16: ОБЩИЕ ИНДЕКСЫ КОЛИЧЕСТВЕННЫХ И КАЧЕСТВЕННЫХ ПОКАЗАТЕЛЕЙ Типичным индексом количественных показателей является индекс физического объёма продукции. Сложность при построении этого индекса заключается в том, что объёмы разных видов продукции (товаров) в натуральном выражении несоизмеримы и суммироваться не могут. В связи с этим для разнородных видов продукции (товаров) нельзя построить общий индекс физического объёма. Здесь требуется использование специальных приёмов индексного метода анализа. Единство разнородных видов продукции (товаров) состоит в том, что они являются продуктами общественного труда, т. е. имеют себестоимость, трудоёмкость, цену. Эти качественные показатели и могут быть использованы в качестве общей меры разнородных видов продукции (товаров). Умножая объём продукции каждого вида на соответствующую себестоимость, трудоёмкость, цену единицы продукции получают сравнимые показатели, которые можно суммировать и анализировать. Для того чтобы индекс охарактеризовал изменение только одного фактора, нужно устранить в формуле влияние другого фактора, зафиксировав его в числителе и знаменателе на уровне одного и того же периода. Агрегатный индекс физического объёма продукции выглядит следующим образом:  .Этот индекс показывает, на сколько процентов (во сколько раз) изменился физический объём продукции в отчётном периоде по сравнению с базисным. Изменение цен на продукцию в отчётном периоде по сравнению с базисным не влияет на значение индекса. При построении агрегатного индекса физического объёма продукции в качестве весов может быть использована себестоимость единицы продукции  или трудоёмкость  .Каждый качественный показатель связан с тем или иным количественным показателем. Рассмотрим принципы построения агрегатных индексов качественных показателей на примере индекса цен. Так как этот индекс характеризует изменение цен, индексируемой величиной в нём будет цена продукции (товара), а весом – количество проданной продукции (товара). Агрегатный индекс цен был предложен в 1874 г. немецким экономистом Г. Пааше и носит его имя.  . Индекс цен Пааше показывает на сколько процентов (во сколько раз) изменился в среднем уровень цен на продукцию (товар), реализованную в отчётном периоде, т. е. экономический эффект от изменения цен. Надо отметить, что указанный выбор весов при построении агрегатного индекса цен нельзя считать обязательным во всех случаях. В статистике многие задачи могут быть решены по-разному в зависимости от конкретных целей и особенностей исследования. Производство любой продукции связано с материальными и трудовыми затратами. Формула агрегатного индекса себестоимости продукции имеет вид:  . Индекс показывает, на сколько процентов (во сколько раз) уменьшился (возрос) в среднем уровень себестоимости. Агрегатный индекс трудоёмкости выглядит следующим образом:  ВОПРОС 17: ИНДЕКСЫ СРЕДНИХ ВЕЛИЧИН Все агрегатные индексы – это индексы постоянного состава, т. к они характеризуют изменение каких-либо признаков – объёма, цен, себестоимости, трудоёмкости при неизменном составе явления. Статистика определяет также индексы средних величин. Но величина средней изменяется под влиянием двух факторов: уровня признака и численности групп (состава и структуры явления). В связи с этим индексы средних величин называются индексами переменного состава. Поскольку средняя величина изменяется под влиянием двух факторов, то статистика, рассчитывая индекс средней величины, выявляет, как повлияло на изменение средней величины изменение уровня признака, для чего она исчисляет агрегатный индекс этого признака, а также то, как повлияло на изменение средней изменение состава явление, для чего исчисляется индекс структурных сдвигов. Такой анализ факторов изменения средних величин проводится при изучении средних цен реализации, средней себестоимости, трудоёмкости урожайности сельскохозяйственных культур и других качественных характеристик. Рассмотрим построение и содержание индексов средних величин на примере индекса средних цен реализации. Определим значения средних цен реализации.    С помощью индекса переменного состава рассчитаем общее изменение средних цен за анализируемый период.  С помощью индекса постоянного состава определим влияние на изменение средней цены изменения цен на отдельные детали.  С помощью индекса структурных сдвигов определим влияние изменения объёмов и структуры производства продукции на изменение средних цен реализации.  Взаимосвязь индексов: 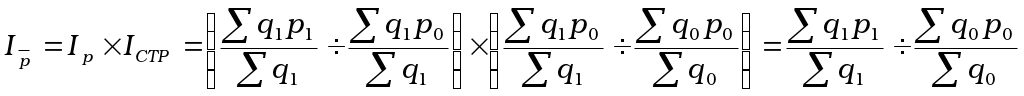 ВОПРОС 18: ПОНЯТИЕ О РЯДАХ ДИНАМИКИ. АНАЛИТИЧЕСКИЕ ПОКАЗАТЕЛИ РЯДА ДИНАМИКИ Ряд динамики – это ряд последовательных значений, характеризующих изменение показателя во времени. Ряд динамики состоит из двух частей: промежутков или моментов времени, к которым относятся уровни и самих уровней. Первая цифра ряда динамики называется начальным уровнем (У0), последняя – конечным (Уn). Для выяснения характера и интенсивности изменения изучаемого явления ряда динамики подвергается глубокому статистическому анализу. В процессе сопоставления абсолютных уровней получаются показатели ряда динамики: абсолютные приросты (А) – это разность между уровнями ряда, которые показывают, насколько один уровень больше или меньше другого. Применяют два способа сравнения: базисный и цепной. Сравниваемый уровень принято называть отчётным, а уровень, с которым происходит сравнение, базисным. При базисном способе сравнения каждый уровень динамического ряда сопоставляется с одним и тем же предшествующим уровнем, принятым за базу сравнения. При цепном способе каждый уровень динамического ряда сравнивается с непосредственно ему предшествующим. Абсолютный прирост Абсолютный прирост базисный цепной А1 = У1 – У0 А1 = У1 – У0 А2 = У2 – У0 А2 = У2 – У1 А3 = У3 – У0 и т. д. А3 = У3 – У2 и т. д. темп роста (ТР) – это относительное изменение уровней ряда динамики. Выражается в коэффициентах или процентах. Коэффициенты (КР) показывают, во сколько раз один уровень больше или меньше другого. Темпы изменения в процентах показывают, сколько процентов составляет один уровень по сравнению с другим. Коэффициент роста Коэффициент роста базисный цепной     и т. д.  и т. д. темп прироста (ТПР) – даёт относительную оценку скорости изменения уровня ряда в единицу времени. Выражается в коэффициентах или процентах и показывает во сколько раз или на сколько процентов сравниваемый уровень больше или меньше уровня, принятого за базу сравнения.  или  абсолютное значение 1 % прироста (П) применяется для того, чтобы правильно оценить значение полученного темпа прироста. В каждом периоде определяется как отношение цепного абсолютного прироста данного периода к цепному темпу прироста.  Для обобщающей характеристики динамики исследуемого явления определяют средние показатели: средний уровень ряда, средний абсолютный прирост, средний темп роста, средний темп прироста. Средний уровень ряда характеризует обобщённую величину абсолютных уровней. Для интервальных рядов динамики при равных интервалах рассчитывается по формуле средней арифметической простой:  Средний абсолютный прирост – это обобщающий показатель скорости изменения уровней во времени.  .Средний темп роста – это сводный обобщающий показатель интенсивности изменения уровней ряда динамики. Вычисляется по формуле средней геометрической:  .Средний темп прироста характеризует среднюю относительную скорость роста (снижения) уровня.  . |