Вопрос Матрица, основные понятия, действия. Матрица
 Скачать 3.78 Mb. Скачать 3.78 Mb.
|
|
Вопрос 1. Матрица, основные понятия, действия. Матрица-это прямоугольная таблица данных. Действия: Сложение (если число столбцов и срок двух матриц равно) Умножение (число столбцов одной равно числу строк другой) Возведение в степень (только квадратные матрицы) Канонический вид- несколько единиц по главной диагонали, остальные нули. Вопрос 2. Определитель ,свойства. Определитель-это алгебраическая сумма произведений всех элементов, стоящих на разных строках и столбцах. Свойства: Равноправие строк и столбцов. Определитель не изменится, если матрицу транспонировать (гл. диаг. на месте). При перестановке двух параллельных рядов матрицы, определитель меняет знак . Определитель матрицы, имеющий 2 одинаковых ряда, равен 0. Общий множитель элементов какого-либо ряда матрицы можно вынести за знак определителя. Если элементы какого-либо ряда определителя представляют собой суммы двух слагаемых, то определитель может быть разложен на сумму двух соответствующих определителей. Определитель не изменится, если к элементам одного ряда прибавить соответствующие элементы параллельного ряда, умноженные на любое число. Определитель равен сумме произведений элементов некоторого ряда на соответствующие им алгебраические дополнения 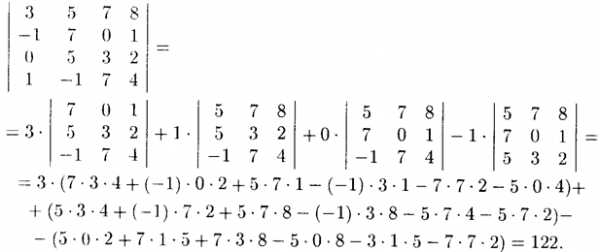 Сумма произведений элементов какого-либо ряда определителя на алгебраические дополнения соответствующих элементов параллельного ряда равна нулю. Вопрос 3. Вычисление опр. третьего порядка. По правилу треугольника. 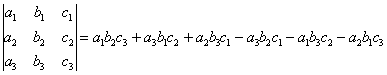 Вопрос 4. Разложение определителя по строке или столбцу. Определитель равен сумме произведений элементов некоторой строки или столбца на алгебраические дополнения этих элементов. строки: 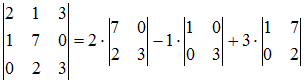 Вопрос 5. Системы линейных уравнений, основные понятия. СЛУ - это объединений из n линейных уравнений , каждое из которых содержит k переменных. Решение СЛУ - это последовательность чисел (k1, k2, ..., kn), которая является решением каждого уравнения системы, т. е. при подстановке в это уравнение вместо переменных x1, x2, ..., xn дает верное числовое равенство. Вопрос 6. Системы однородных линейных алгебраических уравнений. Система линейных уравнений является однородной, если свободный член каждого уравнения системы равен нулю. Например: 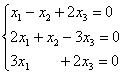 (записываем в виде матрицы, решаем методом Гаусса) Вопрос 7. Теорема Кронекера-Капелли. Система линейных алгебраических уравнений совместна тогда и только тогда, когда ранг её основной матрицы равен рангу её расширенной матрицы. Расширенная матрица (когда за вертикальной линией ей решение)  Основная матрица (без вертикальной линии и решения) 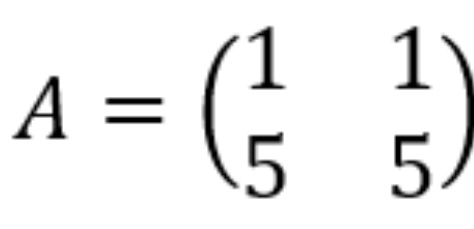 Матрица совместна - имеет решение Ранг матрицы - это максимальное количество линейно зависимых строк. (колво ступенек где нет нулей) Вопрос 8- 9. Метод Гаусса. Возможные действия. Смена мест двух строк. Умножение строки на некоторое число неравное нулю. Прибавление к элементам одной строки соответствующие элементы другой. Вычеркивание строки, все элементы которой равны 0. Вопрос 10. Метод Крамера. Рассмотрим систему уравнений 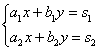 На первом шаге вычислим определитель 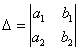 , его называют главным определителем системы. , его называют главным определителем системы. Если Если 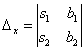 и и 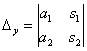 На практике вышеуказанные определители также могут обозначаться латинской буквой Корни уравнения находим по формулам: 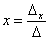 , , 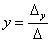 11. Векторы, основные понятия Скалярная величина - величина, которая может быть охарактеризована числом. Например, длина, площадь, масса, температура и т.д. Вектором называется направленный отрезок АВ; точка А - начало, точка В - конец вектора Если начало и конец вектора совпадают, то такой вектор называется нулевым. Чаще всего нулевой вектор обозначается как 0. Векторы называются коллинеарными, если они лежат либо на одной прямой, либо на параллельных прямых Два коллинеарных вектора а и b называются сонаправленными, если их направления совпадают: Два коллинеарных вектора а и b называются противоположно направленными, если их направления противоположны Векторы называются компланарными, если они параллельны одной плоскости или лежат в одной плоскости. Длиной (модулем) вектора АВ называется расстояние между его началом и концом. Вектор, длина которого равна единице, называется единичным вектором или ортом. Векторы называются равными, если они лежат на одной или параллельных прямых; их направления совпадают и длины равны. Иначе говоря, два вектора равны, если они коллинеарны, сонаправлены и имеют равные длины. Проекцией вектора на ось называется разность проекций конца вектора и его начала. О  бозначение-ах бозначение-ахН  аправляющие косинусы аправляющие косинусы12.Линейные операции над векторами. Основные свойства Сложение векторов коммутативно Сложение векторов ассоциативно Прибавление нулевого вектора к любому вектору, не меняет последнего Для любого вектора вектор является противоположным Умножение вектора на число ассоциативно Умножение вектора на число дистрибутивно по отношению к сложению чисел Умножение вектора на число дистрибутивно по отношению к сложению векторов Умножение вектора на единицу не меняет вектора 13. Скалярное произведение векторов, основные свойства Скалярным произведением двух нулевых векторов называют число, которому равно произведение этих двух векторов на косинус угла между ними. Основные свойства:  14. Скалярное произведение в координатной форме. 15. Физические и геометрические приложения скалярного произведения. Угол между векторами Проекция вектора на заданное направление Работа постоянной силы  16. Векторное произведение, основные свойства. Векторным произведением двух векторов →a и →b, которые заданы в прямоугольной системе координат трехмерного пространства, называется такой вектор →c, что: он является нулевым, если векторы →a и →b коллинеарны; он перпендикулярен и вектору →a и вектору →b; векторное произведение длина векторного произведения равна произведению длин векторов →a и →b на синус угла между ними тройка векторов →a, →b, →c ориентирована так же, как и заданная система координат. Свойства 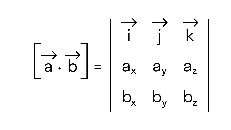 17. Векторное произведение в координатной форме. В прямоугольной системе координат трехмерного пространства векторное произведение двух векторов →a = (ax, ay, az) и →b = (bx, by, bz) есть вектор Это определение показывает нам векторное произведение в координатной форме. Векторное произведение удобно представлять в виде определителя квадратной матрицы третьего порядка, первая строка которой есть орты →i, →j, →k, во второй строке находятся координаты вектора →a, а в третьей — координаты вектора →b в заданной прямоугольной системе координат: 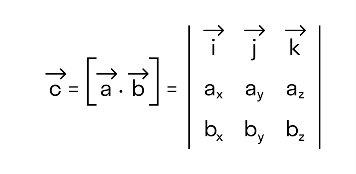 18. Физические и геометрические приложения векторного произведения 1. Условие коллинеарности векторов. Если а параллельно b, то а*b=0 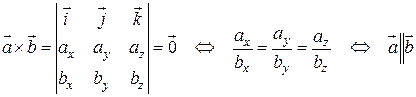 2. Нахождение площади параллелограмма и треугольника. Согласно определению векторного произведения векторов, Физический смысл    19. Смешанное произведение Определение. Смешанным произведением трех векторов
 20. Смешанное произведение в координатной форме. Если известны координаты векторов 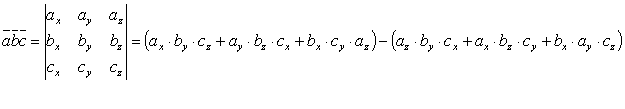 21. Физические и геометрические приложения смешанного произведения. Некоторые приложения смешанного произведения Определение взаимной ориентации векторов в пространстве Определение взаимной ориентации векторов Установление компланарности векторов Векторы 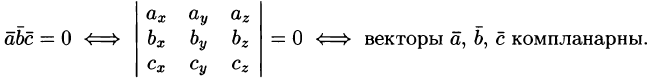 Определение объемов параллелепипеда и треугольной пирамиды Нетрудно показать, что объем параллелепипеда, построенного на векторах ЗАДАНИЯ 22-25 26. Общим уравнением плоскости называется линейное уравнение вида:
где A, B, C, D − некоторые постоянные, причем хотя бы один из элементов A , B и C отлично от нуля. Теорема 1(Необязательно. Написала чтоб было представление). В произвольной декартовой прямоугольной системе координат в пространстве каждая плоскость α может быть задана линейным уравнением (1). Обратно, каждое линейное уравнение (1) в произвольной декартовой прямоугольной системе координат в пространстве определяет плоскость. 27. Различные способы задания прямой и плоскости в пространстве: Способы задания плоскостей: 1. Три различные точки (Через три различные точки в пространстве проходит одна и только одна плоскость.) 2.Прямая линия и точка не лежащая на этой прямой(.Через прямую и точку, не лежащую на этой прямой, проходит одна и только одна плоскость.) 3.Две пересекающиеся прямые (Через две пересекающиеся прямые проходит одна и только одна плоскость, содержащая обе эти прямые.) 4.Две параллельные прямые ( Через две параллельные прямые проходит одна и только одна плоскость, содержащая обе эти прямые.) Способы задания прямой: Двумя точками Двумя пересекающимися плоскостями 28.Типы уравнений прямой в пространстве Прямую линию в пространстве можно задавать в виде: 1) линии пересечения двух не совпадающих и не параллельных плоскостей Р1 и Р2 : 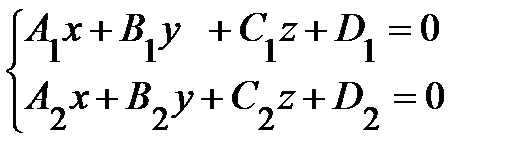 2) уравнения прямой, проходящей через данную точку М(х0 , у0, z0) в направлении, задаваемом вектором L= (m, n, p): 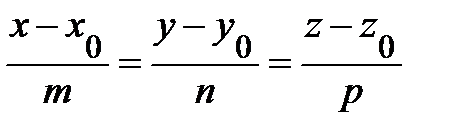 , ,которое называется каноническим уравнением прямой в пространстве; 3) уравнения прямой, проходящей через две заданные точки М(х1, у1, z1) и M(x2, y2, z2): 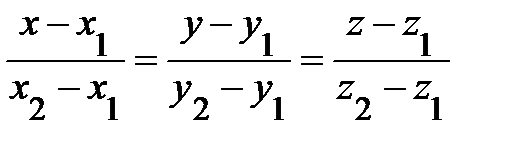 ; ;4) параметрических уравнений: 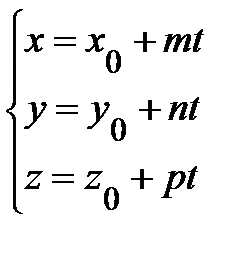 . .29.Типы уравнений плоскости в пространстве 1.Общее уравнение плоскости: Ах + Ву + Сz + D= 0 2. Уравнение плоскости, проходящей через заданную точку М(х0, у0, z0): А(х- х0) + В(у-у0) + С(z-z0) = 0. 3. Уравнение плоскости в отрезках 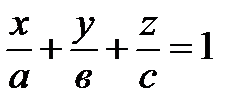 , ,где 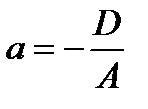 ; ; 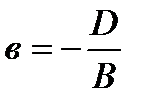 ; ; 4. Уравнение плоскости, проходящей через три заданные точки, не лежащие на одной прямой, записывается в виде определителя 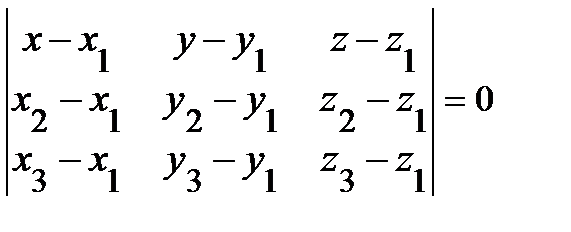 , ,где (х1, y1, z1), (х2, y2, z2), (х3, y3, z3) - координаты заданных точек. 30. Взаимное расположение плоскостей 1. Плоскости параллельны(нет общих точек) 2.Плоскости пересекаются(множество общих точек, лежащих на одной прямой) 3.Плоскости совпадают 31.Взаимное расположение прямых в пространстве 1.Параллельны (нет общих точек. Лежат в одной плоскости) 2.Пересекаются(имеют одну общую точку) 3. Скрещиваются (нет общих точек, не лежат в одной плоскости) ЗАДАНИЕ 32 33. Расстояние от точки до прямой в пространстве. Определение 1 Расстоянием от точки М1 к прямой a называется расстояние между точками М 1 и Н1. Определение 2 Расстоянием от точки до прямой называют длину перпендикуляра, проведенного из данной точки к данной прямой. Первый способ нахождения расстояния от точки Так как по определению расстояние от точки М1 до прямой a – это длина перпендикуляра M1H1, то, определив координаты Второй способ. Итак, чтобы найти расстояние от точки определить направляющий вектор прямой a ( получить координаты 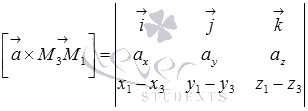 и получить его длину и получить его длину 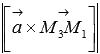 ; ;вычислить требуемое расстояние от точки до прямой в пространстве по формуле 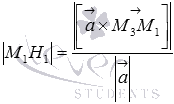 . .34. Расстояние от точки до плоскости в пронстранстве. Формула для вычисления расстояния от точки до плоскости Если задано уравнение плоскости Ax + By + Cz + D = 0, то расстояние от точки M(Mx, My, Mz) до плоскости можно найти, используя следующую формулу:
35. Функция, основные понятия. Обратная функция, сложная функция. 1. Функция — это взаимосвязь между величинами, то есть зависимость одной переменной величины от другой. Знакомое обозначение y = f (x) как раз и выражает идею такой зависимости одной величины от другой. Величина у зависит от величины х по определенному закону, или правилу, которое обозначается f. Вывод: меняя х (независимую переменную, или аргумент) — меняем значение у. 2. Функция — это определенное действие над переменной. Значит, можно взять величину х, как-то над ней поколдовать — и получить соответствующую величину у. В технической литературе можно встретить такие определения функции для устройств, в которых на вход подается х — на выходе получается у. Схематично это выглядит так: В этом значении слово «функция» используют и в далеких от математики областях. Например, так говорят о функциях ноутбука, костей в организме или даже о функциях менеджера в компании. В каждом перечисленном случае речь идет именно о неких действиях. 3. Функция — это соответствие между двумя множествами, причем каждому элементу первого множества соответствует один элемент второго множества. Это самое популярное определение в учебниках по математике. Например, в функции у = 2х каждому действительному числу х ставит в соответствие число в два раза большее, чем х. Обра́тная фу́нкция — функция, обращающая зависимость, выражаемую данной функцией. ложная функция — это функция от функции. Если u — функция от x, то есть u=u (x), а f — функция от u: f=f (u), то функция y=f (u) — сложная. А u в этом случае называют промежуточным аргументом. Еще часто f называют внешней функцией, а u — внутренней 36. Конечный предел функции по Гейне и по Коши, эквивалентность определений.  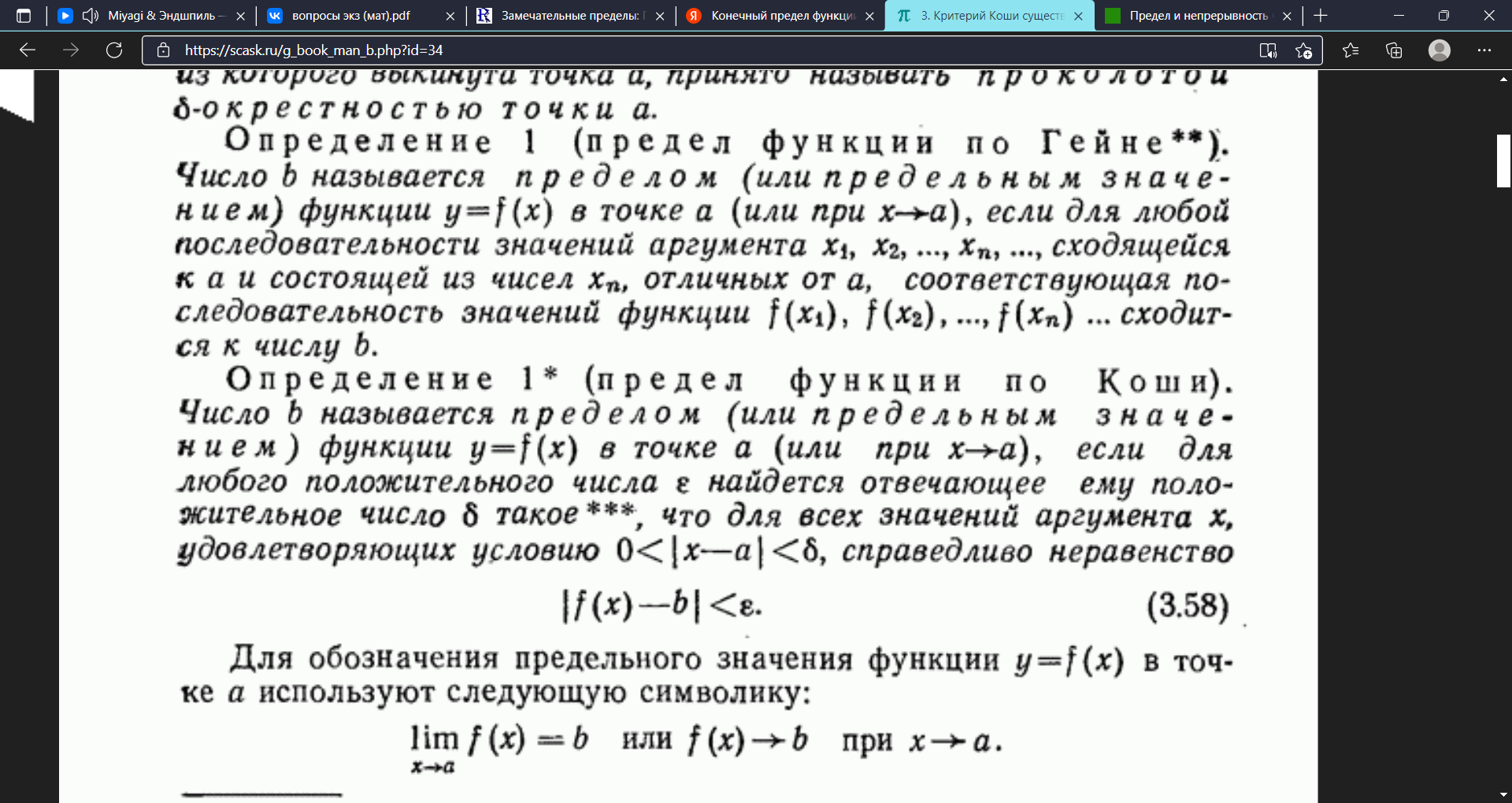 37. Основные свойства функции, имеющей конечный предел: предельный переход в неравенствах и арифметические операции, единственность предела функции. Теорема о единственности предела Формулировка: Если функция f(x) в точке A имеет предел, то этот предел единственный. Доказательство:  38. Первый и второй замечательные пределы. Первый замечательный предел имеет вид 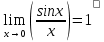 . .Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 0. Второй замечательный предел имеет вид 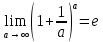 , где e = 2,718281828… – это иррациональное число. , где e = 2,718281828… – это иррациональное число.Вместо переменной х могут присутствовать различные функции, главное, чтобы они стремились к 39. Бесконечно большие функции, бесконечные односторонние пределы. Бесконечно большие функции Определение: Функция Рассмотрим свойства бесконечно больших функций: 1. Сумма бесконечно больших при Замечание: При вычислении разности бесконечно больших функций может получиться любое вещественное число. 2. Произведение бесконечно больших функций есть бесконечно большая функция. Замечание: При вычислении отношения бесконечно больших функций может получиться любое вещественное число. 3. Произведение бесконечно большой функции на ограниченную функцию есть бесконечно большая функция. 35. Вычисление произведения бесконечно большой функции на бесконечно малую функцию может привести к любому вещественному числу. 4. Отношение бесконечно большой функции к ограниченной функции есть бесконечно большая функция. Бесконечные односторонние пределы. Как и обычные пределы, односторонние пределы могут быть бесконечны. Строгие формальные определения односторонних бесконечных пределов приведены в приложении 1. Рассмотрим сначала бесконечные пределы функции в точке справа. Пусть функция /(х) определена в некоторой правой полуокрестности точки а , за исключением, возможно, самой точки а . Функция /(х) имеет в точке а справа бесконечный предел, если при неограниченном приближении значений аргумента х к числу а со стороны значений, больших а , соответствующие значения функции по модулю неограниченно увеличиваются. Тот факт, что функция f(x) имеет в точке а справа бесконечный предел, обозначается записью иначе пишется, что /(х) —> оо при х —> а + 0, или f{a + 0) = оо. Пример 1. Функция 1/ х имеет в точке 0 справа бесконечный предел:  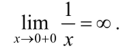 Вполне аналогично формулируются и понятия бесконечных пределов определенного знака в точке справа: функция /(х) имеет в точке а справа предел, равный + оо (равный - оо), если при неограниченном приближении значений аргумента х к числу а со стороны значений, больших а, соответствующие значения функции /(х) неограниченно увеличиваются (становятся отрицательными и по модулю неограниченно увеличиваются). Пример 2. Очевидно, что равенство, приведенное в примере 1 настоящего параграфа, может быть уточнено следующим образом: 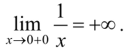 Пример 3. Имеет место равенство Аналогичным образом вводятся понятия бесконечных пределов функции в точке слева. Для этого требуется, чтобы функция /(х) была определена в некоторой левой полуокрестности точки а , за исключением, возможно, самой точки а. Вопрос 40. БМФ, теорема связи между функцией её пределом и БМФ. БМФ имеет вид: 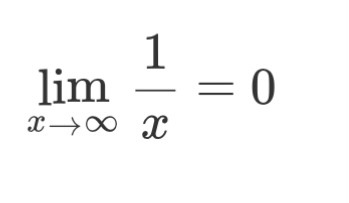  Вопрос 41. Сравнение БМФ, порядок малости, эквивалентные БМФ.  Вопрос 42. Непрерывность функции в точке, арифметические действия над непрерывными функциями. Функция f(x) называется непрерывной в точке α, если: функция f(x) определена в точке α и ее окрестности; существует конечный предел функции f(x) в точке α; э то предел равен значению функции в точке α, т.е. -Ф. называется непрерывной в интервале , если она непрерывна в каждой точке этого интервала. (ab) -Ф. называется непрерывной на отрезке, если она непрерывна на интервале (ab) и в точке x=a непрерывна справа. [ab]   Вопрос 43. Определение и классификация точек разрыва. Если односторонние пределы конечны и не равны между собой , то функция терпит разрыв 1-го рода. 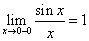 , ,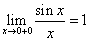  Если односторонние пределы конечны и равны, но сама функция не существует в этой точке , хотя определена в ее окрестностях , то такая точка – точка устранения разрыва. Если пределы функции точки слева и справа не конечны (хотя бы один из односторонних пределов), то такая функция называется точкой разрыва 2-го рода. Вопрос 44. Приращение аргумента, приращение функции в точке, определение производной. Физический смысл производной. Разность x1−x0 называют приращением аргумента (при переходе от точки x0 к точке x1), а разность f(x1)-f(x0) называют приращением функции.( приращение- разность/дельта) П 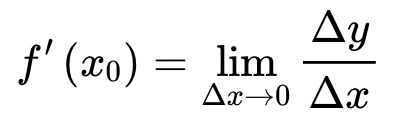 роизводная функции-это предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю. роизводная функции-это предел отношения приращения функции к приращению аргумента, когда последний стремится к нулю.Физический смысл производной – это скорость изменения величины или процесса. Если точка движется вдоль оси х и ее координата изменяется по закону x(t), то мгновенная скорость точки: v(t) = x’(t)=S Вопрос 45. Дифференцируемость функции в точке, необходимое и достаточное условие дифференцируемости функции, связь между непрерывностью и дифференцируемостью функции. Функция f(x) называется дифференцируемой в точке х0, если ее приращение представимо в виде
где A — число, не зависящее от Δх, а o(Δx) — функция более высокого порядка малости чем Δx при Δх → 0 . Необходимое и достаточное условие дифференцируемости Теорема 0.1. Для того, чтобы функция f(x) была дифференцируема в точке x0, необходимо и достаточно, чтобы в этой точке она имела конечную производную. При этом Δf = f'(x0) · Δx + o(Δx) , Следствие. Функция, дифференцируемая в точке, непрерывна в этой точке. Замечание. Дифференциалом dx независимой переменной будем считать приращение Δx, т.е. dx ≡ Δx Отсюда следует формула для вычисления дифференциала
Вопрос 46. Производная суммы, разности, произведения и частного функций. (u + v)’ = u’ + v’, (u - v)’ = u’ - v’. (u * v)’ = u’ v - v’ u. (u / v)’ = (u’ v + v’ u) / v2. ВОПРОСЫ 47-51 52. Правило раскрытия неопределённостей Лопиталя типа 0/0 и ∞/∞ Неопределенность вида бесконечность/бесконечность сводится к неопределенности вида 0/0 простым преобразованием: 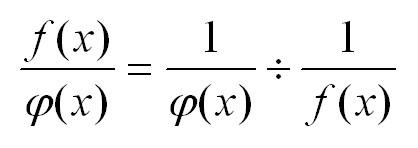 Пусть есть произведение двух функций, одна из которых первая стремиться к нулю, а вторая – к бесконечности. Применяем преобразование, и произведение нуля и бесконечности превращается в неопределенность 0/0: 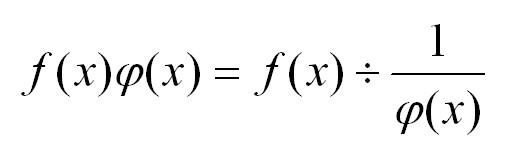 Для нахождения пределов с неопределенностями типа бесконечность минус бесконечность используем следующее преобразование, приводящее к неопределенности 0/0: 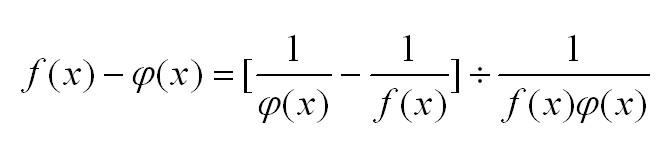 Пример 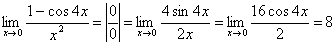 53. Возрастание и убывание функций.  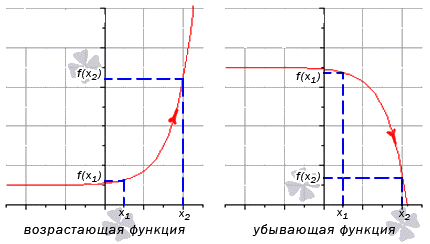 54. Максимум и минимум функций (Экстремумы функции)  Правило исследования функции 1. Найти критические точки функции 2. Выбрать из них лишь те, которые являются внутренними точками области определения функции. 3. Определить знак производной слева и справа от каждой из выбранных критических точек. 4. В соответствии с достаточными условиями экстремума выписать точки экстремума и вычислить значения функции в этих точках. 55. Выпуклость графика функции. Точки перегиба. Выпуклость вверх. Функция выпукла вверх, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит выше проведенного отрезка. Выпуклость вниз. Функция выпукла вниз, если, соединив любые две точки ее графика отрезком прямой, обнаруживают, что соответствующая часть графика лежит ниже проведенного отрезка. Точка перегиба. Точки, в которых выпуклость вверх меняется на выпуклость вниз или наоборот, называются точками перегиба.   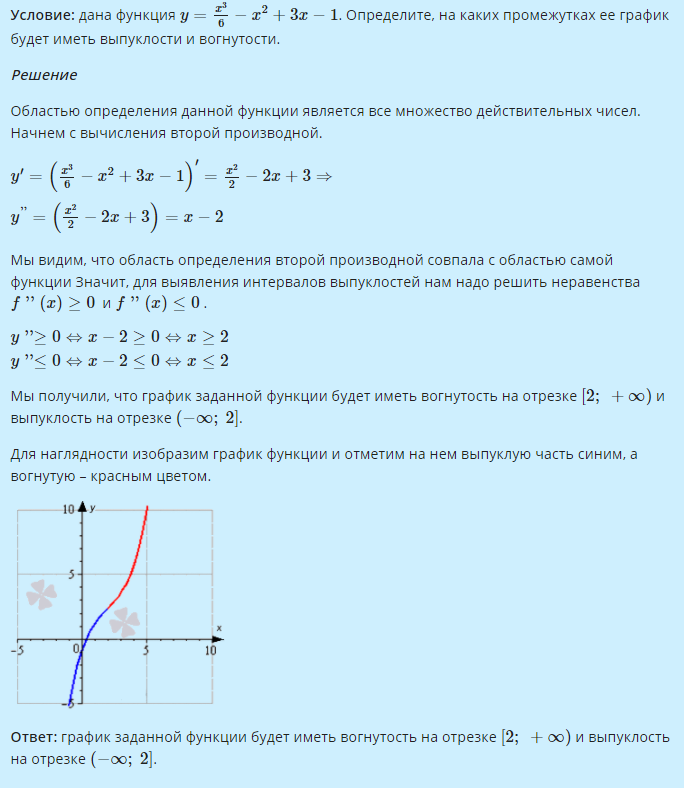 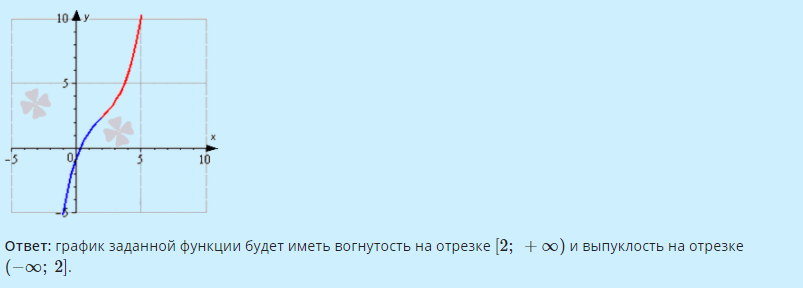 56. Асимптоты графика функции  Вертикальные асимптоты Чтобы найти данный вид асимптот необходимо найти область определения заданной функции и отметить точки разрыва. В этих точках предел функции будет равен бесконечности, а это значит, что функция в этой точке бесконечно приближается к линии асимптоты. Горизонтальные асимптоты Необходимо устремить аргумент лимита функции к бесконечности. Если предел существует и равен числу, то горизонтальная асимптота будет найдена и равна y=y0 как показано во втором столбце таблицы   57. Общая схема исследования функции и построения графика 1. Найти область определения функции. 2. Найти (если это можно) точки пересечения графика с осями координат. 3. Найти интервалы знакопостоянства функции (промежутки, на которых f(x) >О или f(x) <О). 4. Выяснить, является ли функция четной, нечетной или общего вида. 5. Найти асимптоты графика функции. 6. Найти интервалы монотонности функции. 7. Найти экстремумы функции. 8. Найти интервалы выпуклости и точки перегиба графика функции. На основании проведенного исследования построить график функции. Заметим, что приведенная схема исследования не является обязательной. В более простых случаях достаточно выполнить лишь несколько операций, например 1, 2, 7. Если же график функции не совсем 211 понятен и после выполнения всех восьми операций, то можно дополнительно исследовать функцию на периодичность, построить дополнительно несколько точек графика, выявить другие особенности функции. Иногда целесообразно выполнение операций исследования сопровождать постепенным построением графика функции.( общая схема приведена из учебника Письменный)   |
