ВОПРОС 1. Вопрос номенклатура и область применения металлических конструкций. Основные особенности металлических конструкций. Достоинства и недостатки металлических конструкций.
 Скачать 1.77 Mb. Скачать 1.77 Mb.
|
ВОПРОС 15. Работа стержней при кручении.Сопротивляемость кручению отдельных элементов металлических конструкций очень мала, поэтому следует избегать конструктивных решений, допускающих кручение. 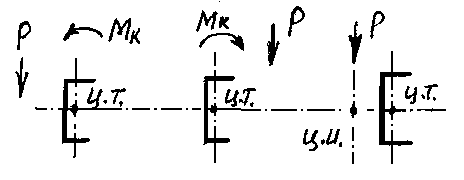 Несимметричная относительно вертикальной оси балка (например, с сечением в виде швеллера), к которой приложена нагрузка, направленная перпендикулярно продольной оси с эксцентриситетом влево или вправо от стенки будет скручиваться соответственно влево или вправо. Существует положение плоскости действия нагрузки, при котором будет только изгиб балки (без кручения). Эта плоскость действия силы пересекает горизонтальную ось симметрии в точке, называемой центром изгиба. Напряжения и деформации при работе элементов на кручения зависят от формы его поперечного сечения. При этом после деформации кручения поперечные сечения не остаются плоскими, депланируют (коробятся). Существуют два вида кручения свободное и стесненное. Свободным кручением называется такой вид кручения, при котором все сечения стержня депланируют одинаково. 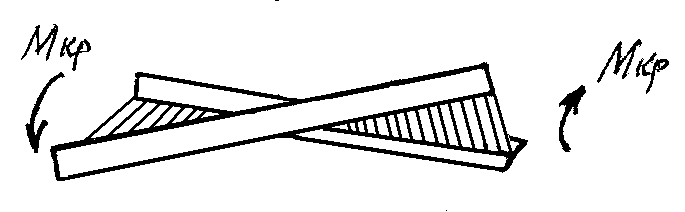 Стесненным, или изгибным, кручением называется такой случай кручения, при котором происходит переменная по длине стержня депланация сечений. 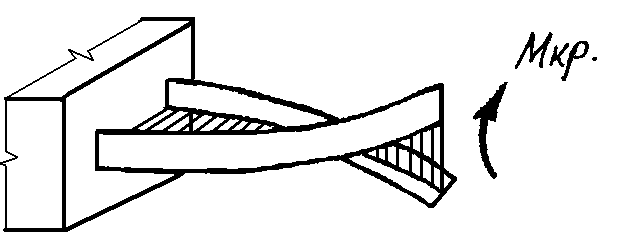 В трубчатом прямоугольном сечении, составленном из пластинок, касательные напряжения, также как и в круглой трубе, распределяются по контуру сечения равномерно по толщине, имея центр в середине контура, а не в центре каждой пластинки. Такое сечение с замкнутым контуром обладает большой сопротивляемостью кручению. Но стоит только этот замкнутый контур разрезать, как сопротивляемость его кручению станет равна сопротивляемости развернутой пластинки. Двутавровые, швеллерные и т.п. профили могут рассматриваться как такие открытые профили. Постановка поперечных диафрагм и особенно поперечных планок, замыкающих в отдельных местах открытый профиль, во много раз увеличивает жесткость элементов при кручении. 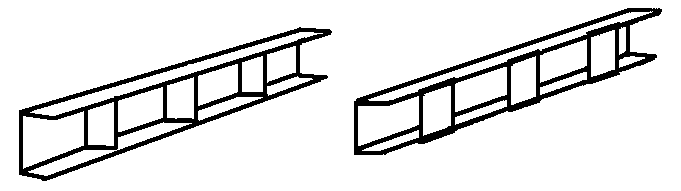 ВОПРОС 16. Устойчивость элементов металлических конструкций. Потеря устойчивости центрально-сжатых стержней. Устойчивость элементов металлических конструкцийИсчерпание несущей способности элемента конструкции может произойти не только в результате разрушения материала, но в результате потери им устойчивости. Потеря устойчивости свойственна относительно тонким и гибким элементам при наличии в них сжимающих напряжений. Потеря устойчивости характеризуется тем, что при увеличении нагрузки после достижения в элементе определенной величины напряжений происходит резкое нарастание искривления элемента, отклонения его от первоначальной формы равновесия, сопровождающееся падением несущей способности. Те силовые воздействия или напряжения, при которых происходит отключение от первоначальной устойчивой формы равновесия, называются критическими: 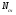 , , 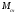 , ,  . .Падение несущей способности элементов при потере устойчивости происходит весьма быстро, без заметных предварительных деформаций, что затрудняет принятие мер по усилению. Неправильный учет критических усилий в металлических конструкциях – одна из наиболее распространенных причин их повреждений и аварий. Потеря устойчивости центрально сжатых стержней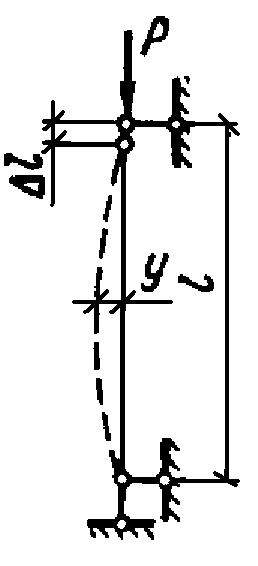 При увеличении силы Р стержень вначале будет оставаться прямым , и если ему даже дать искусственное небольшое отклонение У, то после устранения причины отклонения он вернется к первоначальному прямолинейному положению (устойчивое равновесие). При дальнейшем увеличении внешней нагрузки Р может наступить такой момент, когда будут возможны прямолинейная форма равновесия стержня и криволинейная, изгибная. В этом случае при небольшом искусственном отклонении стержня на величину У и устранения причины отклонения стержень останется изогнутым и не вернется к прямолинейному положению. В точке разветвления прямолинейной криволинейной форм равновесия внешняя сила достигнет своего критического значения Nсч. Дальнейшее, самое незначительное увеличение силы Nсч ведет к резкому нарастанию деформаций и потере несущей способности стержня. Критическая сила для упругого, центрально сжатого, шарнирно – опертого по концам стержня определяется по формуле Л. Эйлера (1744 г.): 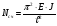 , ,где Е – модуль упругости материала стержня; J – минимальный момент инерции сечения стержня; 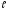 – расчетная длина стержня. – расчетная длина стержня.Критические напряжения в стержне: 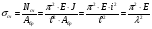 , ,где  – площадь брутто поперечного сечения стержня; – площадь брутто поперечного сечения стержня;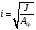 – радиус инерции стержня; – радиус инерции стержня;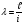 –- гибкость стержня. –- гибкость стержня.Критические напряжения зависят только от гибкости стержня . При выводе формулы Эйлера предполагалось что модуль упругости материала Е имеет постоянное значение. Поэтому для строительных сталей формула справедлива только в пределах пропорциональности. Минимальная гибкость для стального стержня, выше которой формула Эйлера будет справедлива:  . .Абсолютно прямолинейный стержень является идеализированной расчетной схемой. Все реальные стержни в натуре имеют неизбежные отклонения от прямолинейности (случайные эксцентриситеты 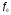 ). Поэтому с самого начала загружения центрально сжатого стержня в нем возникает изгибающий момент ). Поэтому с самого начала загружения центрально сжатого стержня в нем возникает изгибающий момент 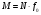 , что ухудшает условия устойчивости стержня и снижает его критические напряжения. Величина случайных эксцентриситетов определяется статистическим изучением реальных стержней. Устойчивость центрально сжатого стержня будет обеспечена, если напряжение в нем будут меньше критических: , что ухудшает условия устойчивости стержня и снижает его критические напряжения. Величина случайных эксцентриситетов определяется статистическим изучением реальных стержней. Устойчивость центрально сжатого стержня будет обеспечена, если напряжение в нем будут меньше критических: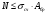 . .Чтобы не определять для каждого стержня критические напряжения, а иметь дело с расчетным сопротивлением стали Ry, критические напряжения выражают через расчетное сопротивление стали, умноженное на коэффициент продольного изгиба (меньший единицы):  . .тогда 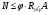 . .Или, переписав это выражение в принятой форме сравнения напряжений в стержне с расчетным сопротивлением стали, получим расчетную формулу проверки устойчивости стержня при центральном сжатии, принятую в нормах:  . .Коэффициент продольного изгиба  принимается по таблицам СНиП в зависимости от класса стали и гибкости элемента принимается по таблицам СНиП в зависимости от класса стали и гибкости элемента 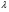 , определяемой по формуле: , определяемой по формуле: , ,где 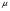 – коэффициент приведения расчетной длины, учитывающий условия закрепления концов стержня; – коэффициент приведения расчетной длины, учитывающий условия закрепления концов стержня;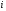 – радиус инерции сечения стержня; – радиус инерции сечения стержня; - расчетная длина стержня; - расчетная длина стержня;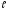 – геометрическая длина стержня. – геометрическая длина стержня.Значения коэффициентов  для сталей разных классов и некоторых алюминиевых сплавов приведены в нормах проектирования. для сталей разных классов и некоторых алюминиевых сплавов приведены в нормах проектирования.ВОПРОС 17. Потеря устойчивости внецентренно сжатых и сжато-изогнутых стержней. |
