Статистика. Вопросы для экзамена по дисциплине статистика
 Скачать 1.31 Mb.
|
|
Средняя арифметическая взвешенная — это средняя из вариантов, которые повторяются разное число раз или имеют различный вес. Она может быть рассчитана по формуле: 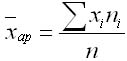 Основные свойства средней арифметической
Часто приходится вычислять среднюю по групповым средним или по средним отдельных частей совокупности. Например, средняя рождаемость в стране представляет собой среднее из средних рождаемости по отдельным регионам страны. Средние из средних определяются так же, как и средние из первоначальных значений признака. 5.Средняя гармоническая: простая и взвешенная, особенности их применения (указать формулы и дать примеры). Средняя гармоническая. Эту среднюю называют обратной средней арифметической, поскольку эта величина используется при k = -1. Простая средняя гармоническая используется тогда, когда веса значений признака одинаковы. Ее формулу можно вывести из базовой формулы, подставив k = -1: 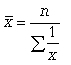 (5.6)К примеру, нам нужно вычислить среднюю скорость двух автомашин, прошедших один и тот же путь, но с разной скоростью: первая - со скоростью 100 км/ч, вторая - 90 км/ч. Применяя метод средней гармонической, мы вычисляем среднюю скорость: 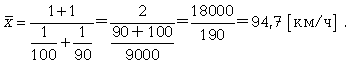 В статистической практике чаще используется 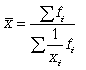 гармоническая взвешенная, формула которой имеет вид (5.7)Данная формула используется в тех случаях, когда веса (или объемы явлений) по каждому признаку не равны. В исходном соотношении для расчета средней известен числитель, но неизвестен знаменатель. Например, при расчете средней цены мы должны пользоваться отношением суммы реализации к количеству реализованных единиц. Нам не известно количество реализованных единиц (речь идет о разных товарах), но известны суммы реализаций этих различных товаров. Допустим, необходимо узнать среднюю цену реализованных товаров:
Получаем 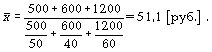 6. Мода и медиана – структурные средние. (указать формулы и дать примеры). Мода и медиана Медиана в статистке Медиана — это такое значение признака, которое разделяет ранжированный ряд распределения на две равные части — со значениями признака меньше медианы и со значениями признака больше медианы. Для нахождения медианы, нужно отыскать значение признака, которое находится на середине упорядоченного ряда. Посмотреть решение задачи на нахождение моды и медианы Вы можете здесь В ранжированных рядах несгруппированные данные для нахождения медианы сводятся к поиску порядкового номера медианы. Медиана может быть вычислена по следующей формуле: 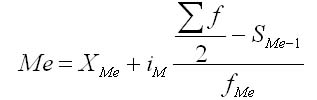 где Хm — нижняя граница медианного интервала; im — медианный интервал; Sme— сумма наблюдений, которая была накоплена до начала медианного интервала; fme — число наблюдений в медианном интервале. Свойства медианы
Графическое определение медианы Для определения медианы графическим методом используют накопленные частоты, по которым строится кумулятивная кривая. Вершины ординат, соответствующих накопленным частотам, соединяют отрезками прямой. Разделив поп олам последнюю ординату, которая соответствует общей сумме частот и проведя к ней перпендикуляр пересечения с кумулятивной кривой, находят ординату искомого значения медианы. Определение моды в статистике Мода — значение признака, имеющее наибольшую частоту в статистическом ряду распределения. Определение моды производится разными способами, и это зависит от того, представлен ли варьирующий признак в виде дискретного или интервального ряда. Нахождение моды и медианы в контрольных по статистике происходит путем обычного просматривания столбца частот. В этом столбце находят наибольшее число, характеризующее наибольшую частоту. Ей соответствует определенное значение признака, которое и является модой. В интервальном вариационном ряду модой приблизительно считают центральный вариант интервала с наибольшей частотой. В таком ряду распределения мода вычисляется по формуле: 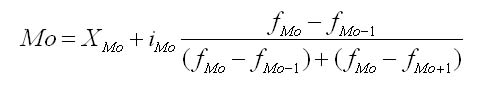 где ХМо — нижняя граница модального интервала; imo — модальный интервал; fм0, fм0-1,, fм0+1 - частоты в модальном, предыдущем и следующем за модальным интервалах. Модальный интервал определяется по наибольшей частоте. Мода широко используется в статистической практике при анализе покупательного спроса, регистрации цен и т. д. 7. Виды динамических рядов .Средняя хронологическая для динамического ряда, методика расчета (указать формулы и дать примеры). Изменение социально-экономических явлений во времени изучается статистикой методом построения и анализа динамических рядов. Ряды динамики - это значения статистических показателей, которые представлены в определенной хронологической последовательности.Каждый динамический ряд содержит две составляющие: 1) показатели периодов времени (годы, кварталы, месяцы, дни или даты); 2) показатели, характеризующие исследуемый объект за временные периоды или на соответствующие даты, которые называют уровнями ряда.Уровни ряда выражаются как абсолютными, так и средними или относительными величинами. В зависимости от характера показателей строят динамические ряды абсолютных, относительных и средних величин. Ряды динамики из относительных и средних величин строят на основе производных рядов абсолютных величин. Различают интервальные и моментные ряды динамики. Динамический интервальный ряд содержит значения показателей за определенные периоды времени. В интервальном ряду уровни можно суммировать, получая объем явления за более длительный период, или так называемые накопленные итоги.Динамический моментный ряд отражает значения показателей на определенный момент времени (дату времени). В моментных рядах исследователя может интересовать только разность явлений, отражающая изменение уровня ряда между определенными датами, поскольку сумма уровней здесь не имеет реального содержания. Накопленные итоги здесь не рассчитываются.8.Основные показатели динамического ряда (указать формулы и дать примеры). 9.Среднегодовые показатели роста и прироста (указать формулы и дать примеры). 4. Динамические (хронологические) средние Важнейшими обобщающими показателями динамического ряда выступают различного рода средние, рассчитываемые как по уровням, так и по производным показателям ряда. Они дают в той или иной степени количественную характеристику действующих в явлениях закономерностей. Средние, подсчитанные по смежным уровням динамического ряда, называются динамическими или хронологическими. Хронологическая средняя отличается от обычной средней тем, что она характеризует явление, относящееся к различным периодам времени, а обычная – к одному периоду времени. Динамические средние должны рассчитываться в пределах качественно однородных периодов: при этом как обычные средние рассчитываются по всей совокупности явлений в целом, так хронологические средние должны исчисляться на основе исчерпывающих данных за весь однородный период. Рассмотрим способы расчета средних абсолютных уровней, средних абсолютных приростов, средних темпов роста и прироста. Средние показатели абсолютных уровней по интервальным и моментным динамическим рядам рассчитываются по-разному. Средний уровень интервального ряда динамики можно подсчитать по формуле:  где у – уровни интервального динамического ряда; t – длительность отдельных интервалов времени. Если интервалы в ряду динамики равные, то формула расчета среднего уровня принимает вид:  где n – число равных промежутков или интервалов. Таблица 1.1 Производство холодильников и морозильников в Республике Беларусь в 2000-2004 гг., (тыс. шт.)
Вычислим по данным табл. 1.1 среднегодовой уровень производства холодильников и морозильников в Республике Беларусь за 1999-2004 гг. 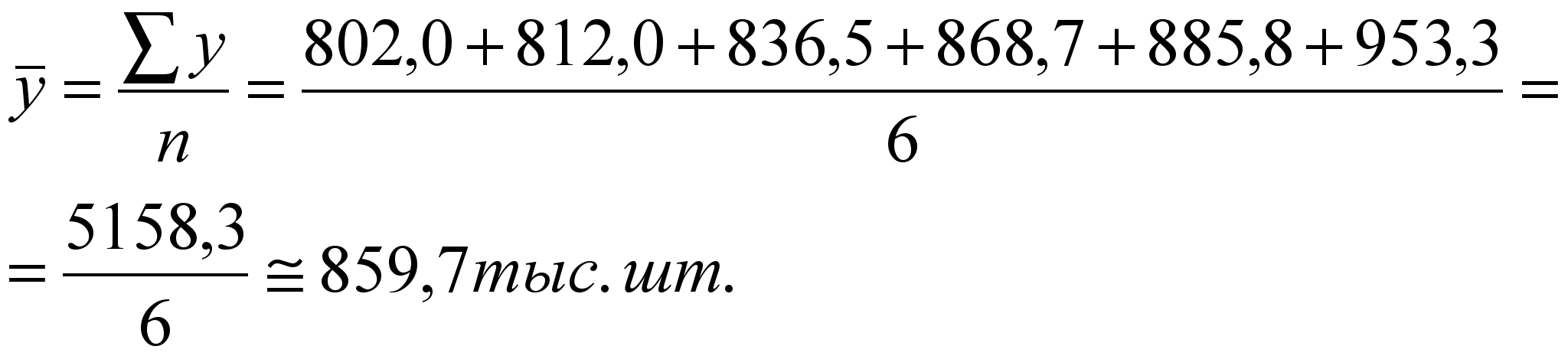  По моментным рядам динамики средний абсолютный уровень рассчитывается по-разному, в зависимости от характера исходных данных. Если уровни моментного ряда динамики даны на даты равноудаленные друг от друга, то в этом случае используется формула расчета среднего уровня вида:  Пример. Имеются следующие данные о наличии товарно-материальных ценностей на начало каждого квартала года: на 01.01.2004 г. – 280 млн. р.; на 1.04. – 300 млн. р.; на 1.07. – 340 млн. р.; на 1.10. – 300 млн. р.; на 1.01.2005 г. – 360 млн. р. Вычислим средний размер остатков товарно-материальных ценностей за 2004 г.: 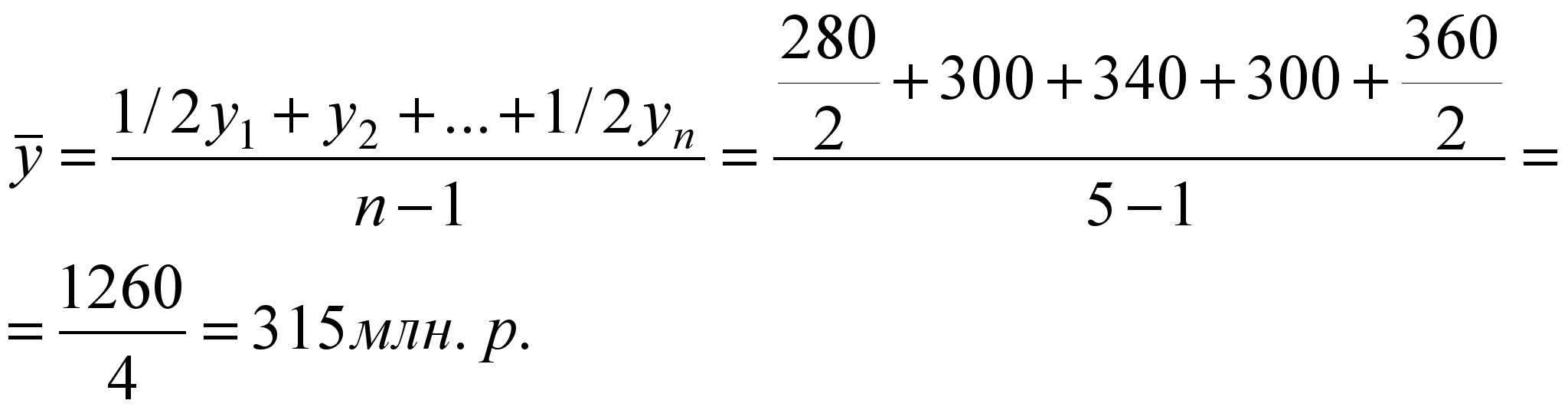 В данной формуле расчета среднего абсолютного уровня знаменатель совпадает с числом интервалов (кварталов), охватываемых рядом. Он меньше на единицу количества данных уровней, так как первый и последний уровни входят в расчет с половинными весами. В тех случаях, когда уровни моментного ряда отстоят друг от друга на разном расстоянии (во времени), то в этих случаях необходимо полусуммы уровней взвешивать по величине интервалов времени между ними: 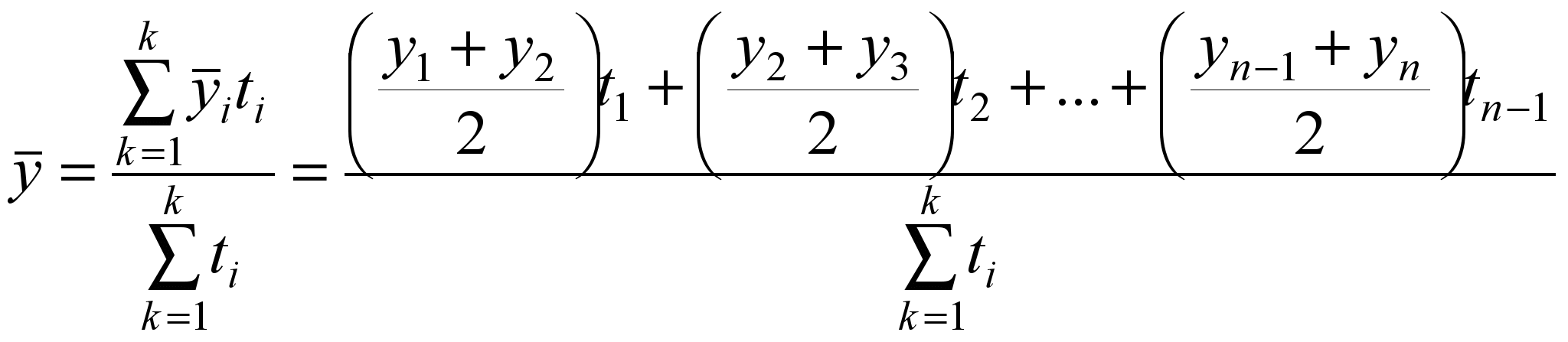 ,где k = n-1. Пример. В результате инвентаризации на заводе установлены следующие остатки товарно-материальных ценностей: на 01.01.2004 г. – 400 млн. р.; на 1.05. – 420 млн. р.; на 1.10. – 440 млн. р.; на 1.01.2005 г. – 430 млн. р. Определим средний размер остатков товарно-материальных ценностей на заводе за 2004 год: 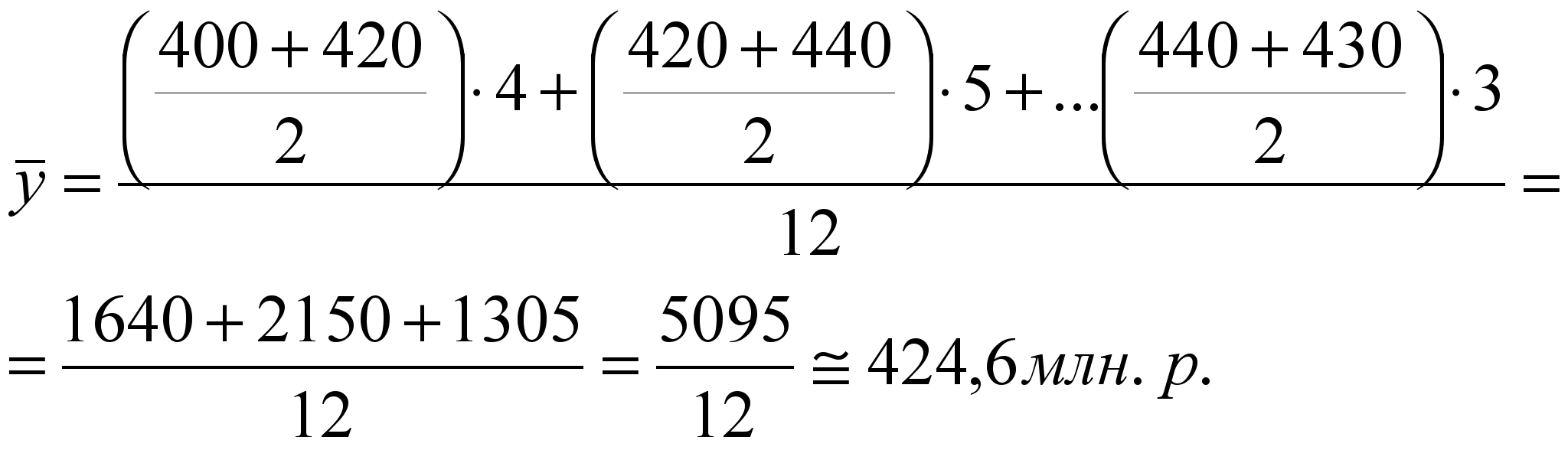 ,Если располагаем исчерпывающими данными об изменении изучаемых явлений, то расчет среднего абсолютного уровня по таким моментным рядам рассчитывается по формуле средней арифметической взвешенной:  ,где у – уровень моментного ряда динамики; t – интервалы (промежутки) времени между ними. Пример. В течение первых пяти дней апреля – с 1 по 5 число включительно – было 1200 человек, в следующие десять дней – с 6 по 15 апреля – 1250 человек и последующие 15 дней, с 16 по 30 апреля – 1300 человек. По этим данным определим среднюю численность рабочих за апрель: 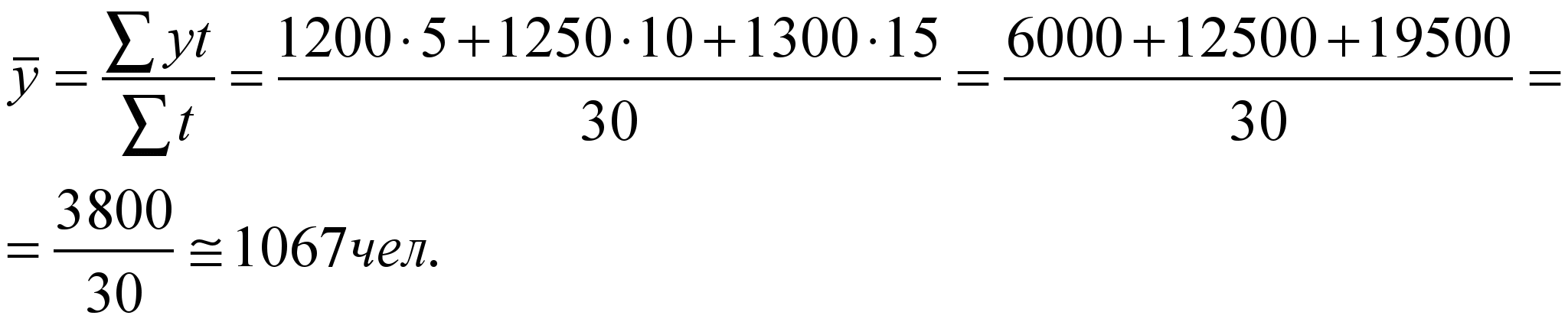 ,Расчет среднего абсолютного прироста. Средний абсолютный прирост можно рассчитать по формулам:  где m = n-1  В обоих случаях получим идентичный результат. Вычислим среднегодовой абсолютный прирост производства холодильников и морозильников в Республике Беларусь за 2000-2004 гг. (по данным табл. 3.1):   Расчет среднего темпа роста и прироста. Средние темпы роста рассчитываются по формуле средней геометрической:  где m – число равных интервалов времени в периоде; Т1, Т2, …, Тm – темпы роста, исчисленные цепным способом. Средний годовой темп роста производства холодильников и морозильников в Республике Беларусь за 2000-2004 гг. можно получить из следующего расчета (табл. 3.1):  Среднегодовой темп прироста составил:  Когда известны уровни динамического ряда, то расчет среднего темпа роста можно произвести по преобразовательной формуле. Подставив в подкоренное выражение вместо Т1, Т2, … их исходные значения  формула расчета среднего темпа роста примет вид: В нашем примере среднегодовой темп роста холодильников и морозильников вычислим так:  Результаты расчета в обоих случаях идентичны. Наряду с формулой средней геометрической простой применяется и формула средней геометрической взвешенной:  Пример. За первые два года пятилетки производство продукции возрастало по 5% в год, а за оставшиеся три года – по 4%.Вычислим среднегодовой темп роста производства продукции за пятилетку в целом:  Расчет средней геометрической на основе суммы членов ряда. В тех случаях, когда известны только базисный уровень и сумма уровней за весь изучаемый период, расчет средней геометрической изменяется по сравнению с ранее рассмотренным случаем. Средний темп роста, определяемый по сумме уровней, назван проф. Казинцом Л.С. параболическим темпом роста. Он исчисляется следующим образом: 1) определяется отношение суммы уровней за период без базисного 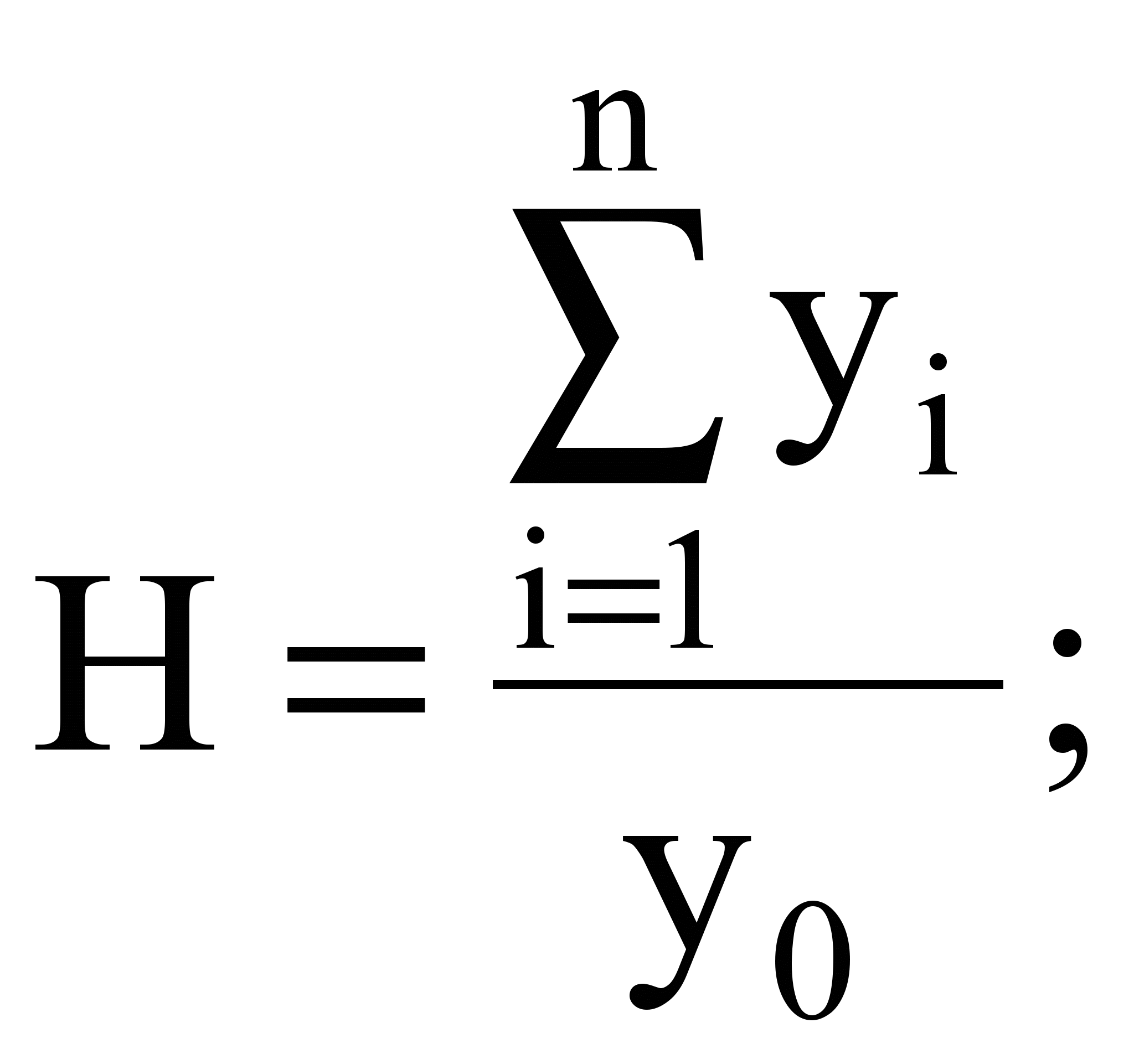 к уровню, принятому за базу сравнения (у0): 2) по таблице, приведенной в книге Л.С. Казинца «Темпы роста и абсолютные приросты» М.: 1975 г. находим столбец, равный числу уровней в периоде (n), в котором величина Н приближается к исчисленному ранее значению. В первом столбце таблицы по этой строке и находим значение параболического среднегодового темпа роста. Пример. Допустим, в 2000 г. было произведено продукции на 114,9 млрд. руб. За 2001-2005 гг. предусматривается произвести продукции в сопоставимых ценах на 621,4 млрд. руб. Каким должен быть среднегодовой темп роста объема продукции, с тем чтобы за пятилетку был достигнут намеченный количественный объем производства продукции? 1) Вычислим отношение суммы уровней за 2001-2005 гг. к уровню 2000 г.:  2) найдем по таблице расчета параболического темпа роста столбец со значением равным в нашем случае 5 число близкое к 5,408. Это будет 5,404. В первом столбце таблицы определим число, стоящее в той же строке, что и 5,404. Оно равно 1,026, или 102,6%. Это число и представляет собой искомый среднегодовой темп роста производства продукции за 2001-2005 гг. 3) вычислим объемы производства продукции по каждому году пятилетки (2001-2005 гг.):
|
1,026=117,9;