Статистика. Вопросы для экзамена по дисциплине статистика

• Название: Вопросы для экзамена по дисциплине статистика
• Анкор: Статистика.docx
• Дата: 30.01.2018
• Размер: 1.31 Mb.
• Имя файла: Статистика.docx
• Тип: Вопросы для экзамена; #15030
• страница: 3 из 7

10. Интерполяция и экстраполяция в динамических рядах (указать формулы и дать примеры).

Интерполяцией называется приблизительный расчет недостающих уровней внутри однородного периода, когда известны уровни по обе стороны неизвестного.

Интерполяция производится исходя из предположения, что изменения в пределах периода, выражающее закономерность развития, относительно устойчивы. Для этого необходимо установить характер динамики, т.е. найти относительно устойчивые производные (средние) показатели: абсолютный прирост, темп роста и др.

Возможны различные варианты интерполяции:

1) рассчитывается средняя арифметическая из прилегающих пропущенному уровней ряда; 

2) при относительной стабильности абсолютных приростов интерполяция уровней ряда осуществляется прибавлением среднего абсолютного прироста к уровню предшествующему пропущенному;

3) при относительной стабильности темпов роста необходимо уровень предшествующей пропущенному умножить на величину среднего темпа роста.

Рассмотрим пример

Таблица 6.1

Год Показатель	1999	2000	2001	2002	2003	2004
Производство холодильников и морозильников, тыс. шт.	802,0	812,0	836,5	868,7	885,8	953,3
Абсолютный прирост	-	10,0	24,5	32,2	17,1	67,5
темп роста, %	-	101,2	103,0	103,8	102,0	107,6

Допустим, пропущен уровень 2002 г.

Используя первый способ интерполяции, определим его как среднюю арифметическую из уровней 2001 и 2003 гг.:



.Произведем интерполяцию по второму способу расчета. Для этого необходимо вычислить среднегодовой абсолютный прирост за 2000-2004 г.:



Уровень 2002 г. определим:



Интерполяция по третьему способу требует предварительного расчета среднегодового темпа роста за 2000-2004 гг.:



Уровень 2002 г. составит:



Сравнивая три способа интерполяции уровня производства холодильников и морозильников для 2002 г., отметим, что наилучшее приближение к фактическому уровню дает расчет по величине среднегодового абсолютного прироста.

Экстраполяцией называется приблизительный расчет недостающего уровня по одну сторону неизвестного. Если расчет уровней осуществляется на перспективу, то такой способ представляет собой прогнозирование.

Прогноз уровней осуществляется на основе исходного ряда динамики (база прогноза). К нему предъявляется ряд требований:

1) полнота и непрерывность уровней исходного ряда динамики;

2) качественная его однородность с точки зрения наличия общей закономерности развития явлений;

3) число уровней, входящих в исходный ряд динамики должно быть достаточно значительным, с тем чтобы закономерность развития явлений была достаточно четкой и поддавалась количественному измерению.

Идея прогноза базируется на том постулате, что закономерности развития явлений, присущие исходному ряду динамики, сохраняются и в прогнозируемом периоде. При среднесрочном прогнозе рекомендуется прогноз уровней осуществлять не более чем на одну треть длины исходного ряда динамики. Используется дискретные и интервальные методы прогноза уровней социально-экономических явлений. В первом случае для каждого периода времени определяется одно значение прогнозного уровня. Во втором случае, наряду с основными оценками прогноза дается вероятностная интерпретация нижних и верхних границ прогнозных уровней.

Дискретный (точечный) прогноз уровней базируется на характере закономерностей развития явлений в исходном ряду динамики. Если развитие процесса идет по закону арифметической прогрессии (с относительно стабильными абсолютными приростами), то уровни прогноза (точечные) определим по формуле:



где У_i – последний уровень в исходном ряду динамики; t_i – порядковый номер периода прогноза (t_i=1,2…n); - средний абсолютный прирост в исходном ряду динамики. 

По данным табл. 6.1 вычислим прогноз производства холодильников и морозильников в Республике Беларусь 2005-2006 гг.:





В рядах динамики, где развитие явлений происходит по закону геометрической прогрессии (с относительно стабильными темпами роста), то уровни прогноза вычислим по формуле:



где - средний темп роста в исходном ряду динамики.

Применительно к нашему примеру (табл. 6.1) будем иметь следующие прогнозные значения производства холодильников и морозильников в Республике Беларусь:





11. Построение индексов цены и физического объема в агрегатной форме. Индексируемая величина и статистический вес (указать формулы и дать примеры).

12. Средние индексы цен и физического объема, тождественные агрегатным

(указать формулы и дать примеры).

13.Выбор базы и весов при построении индексов. Системы индексов : цепных и базисных (указать формулы и дать примеры).

Индексами называют сравнительные относительные величины, которые характеризуют изменение сложных социально-экономических показателей (показатели, состоящие из несуммируемых элементов) во времени, в пространстве, по сравнению с планом.

Индекс - это результат сравнения двух одноименных показателей, при исчислении которого следует различать числитель индексного отношения (сравниваемый или отчетный уровень) и знаменатель индексного отношения (базисный уровень, с которым производится сравнение). Выбор базы зависит от цели исследования. Если изучается динамика, то за базисную величину может быть взят размер показателя в периоде, предшествующем отчетному. Если необходимо осуществить территориальное сравнение, то за базу можно принять данные другой территории. За базу сравнения могут приниматься плановые показатели, если необходимо использовать индексы как показатели выполнения плана.

Индексы формируют важнейшие экономические показатели национальной экономики и ее отдельных отраслей. Индексные показатели позволяют осуществить анализ результатов деятельности предприятий и организаций, выпускающих самую разнообразную продукцию или занимающихся различными видами деятельности. С помощью индексов можно проследить роль отдельных факторов при формировании важнейших экономических показателей, выявить основные резервы производства. Индексы широко используются в сопоставлении международных экономических показателей при определении уровня жизни, деловой активности, ценовой политики и т.д.

Существует два подхода в интерпретации возможностей индексных показателей: обобщающий (синтетический) и аналитический, которые в свою очередь определяются разными задачами.

Суть обобщающего подхода - в трактовке индекса как показателя среднего изменения уровня исследуемого явления. В этом случае основной задачей, решаемой с помощью индексных показателей, будет характеристика общего изменения многофакторного экономического показателя.

Аналитический подход рассматривает индекс как показатель изменения уровня результативной величины, на которую оказывает влияние величина, изучаемая с помощью индекса. Отсюда и иная задача, которая решается с помощью индексных показателей: выделить влияние одного из факторов в изменении многофакторного показателя.

От содержания изучаемых показателей, методологии расчета первичных показателей, целей и задач исследования зависят и способы построения индексов.

По степени охвата элементов явления индексы делят на индивидуальные и общие (сводные).

Индивидуальные индексы (i) - это индексы, которые характеризуют изменение только одного элемента совокупности.

Общий (сводный) индекс (I) характеризует изменение по всей совокупности элементов сложного явления. Если индексы охватывают только часть явления, то их называют групповыми. В зависимости от способа изучения общие индексы могут быть построены или как агрегатные (от лат. аggrega - присоединяю) индексы, или как средние взвешенные индексы (средние из индивидуальных).

Способ построения агрегатных индексов заключается в том, что при помощи так называемых соизмерителей можно выразить итоговые величины сложной совокупности в отчетном и базисном периодах, а затем первую сопоставить со второй.

В статистике имеют большое значение индексы переменного и фиксированного состава, которые используются при анализе динамики средних показателей.

Индексом переменного состава называют отношение двух средних уровней.

Индекс фиксированного состава есть средний из индивидуальных индексов. Он рассчитывается как отношение двух стандартизованных средних, где влияние изменения структурного фактора устранено, поэтому данный индекс называют еще индексом постоянного состава.

В зависимости от характера и содержания индексируемых величин различают индексы количественных (объемных) показателей и индексы качественных показателей.

10.2.

Индексы количественных показателей

К индексам количественных (объемных) показателей относятся такие индексы, как индексы физического объема производства продукции, затрат на выпуск продукции, стоимости продукции, а также индексы показателей, размеры которых определяются абсолютными величинами. Используются различные виды индексов количественных показателей.

Индекс физического объема продукции (ФОП) отражает изменение выпуска продукции.

Индивидуальный индекс ФОП отражает изменение выпуска продукции одного вида и определяется по формуле

 (10.1)

где q₁ и q₀ - количество продукции данного вида в натуральном выражении в текущем и базисном периодах.

Агрегатный индекс ФОП (предложен 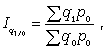Э. Ласпейресом) отражает изменение выпуска всей совокупности продукции, где индексируемой величиной является количество продукции q, а соизмерителем - цена р:

 (10.2)

где q₁ и q₀ - количество выработанных единиц отдельных видов продукции соответственно в отчетном и базисном периодах; p₀ - цена единицы продукции (отдельного вида) в базисном периоде.

При вычислении индекса ФОП в качестве соизмерителей может выступать также себестоимость продукции или трудоемкость.

Средние взвешенные индексы ФОП используются в том случае, если известны индивидуальные индексы объема по отдельным видам продукции и стоимость отдельных видов продукции (или затраты) в базисном или отчетном периоде.

Средний взвешенный арифметический индекс ФОП определяется по формуле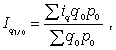

 (10.3)

где i_q - индивидуальный индекс по каждому виду продукции; q₀ p₀ - стоимость продукции каждого вида в базисном периоде.

Средний взвешенный гармонический индекс ФОП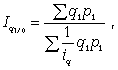

 (10.4)

где q₁ p₁ - стоимость продукции каждого вида в текущем периоде.

Аналогично рассчитывается индекс затрат на выпуск продукции (ЗВП), который отражает изменение затрат на производство и может быть как индивидуальным, так и агрегатным.

Индивидуальный индекс ЗВП отражает изменение затрат на производство одного вида и определяется по формуле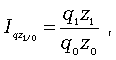

 (10.5)

где z₁ и z₀ - себестоимость единицы продукции искомого вида в текущем и базисном периодах; q₁ z₁ и q₀ z₀ - суммы затрат на выпуск продукции искомого вида в текущем и базисном периодах.

Агрегатный индекс ЗВП характеризует изменение общей суммы затрат на выпуск продукции за счет изменения количества выработанной продукции и ее себестоимости и определяется по формуле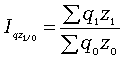

(10.6)

где q₁ z₁ и q₀ z₀ - затраты на выпуск продукции каждого вида соответственно в отчетном и базисном периодах.

Рассмотрим построение индекса стоимости продукции (СП), который может определяться и как индивидуальный, и как агрегатный.