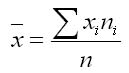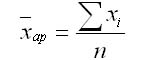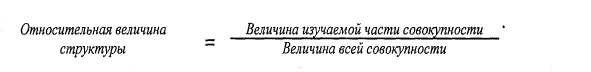ВОПРОСЫ ДЛЯ ЭКЗАМЕНА ПО ДИСЦИПЛИНЕ «СТАТИСТИКА»
для студентов второго курса
1.Формы, виды, способы статистического наблюдения.
Статистическое наблюдение — это массовое (оно охватывает большое число случаев проявления исследуемого явления для получения правдивых статистических данных) планомерное (проводится по разработанному плану, включающему вопросы методологии, организации сбора и контроля достоверности информации), систематическое (проводится систематически, либо непрерывно, либо регулярно), научно организованное (для повышения достоверности данных, которая зависит от программы наблюдения, содержания анкет, качества подготовки инструкций) наблюдение за явлениями и процессами социально-экономической жизни, которое заключается в сборе и регистрации отдельных признаков у каждой единицы сФормы статистического наблюдения
Статистическая отчетность
Основная форма статистического наблюдения, которая заключается в получении статистическими органами данных от единиц наблюдения. Данные поступают в органы статистики от предприятий и организаций в виде обязательных отчетов об их деятельности. Отчётные документы утверждаются Министерством финансов РФ и Госкомстатом РФ. Методы и формы организации статистической отчетности дифференцируются применительно к различным типам предприятий и формам предпринимательства. Основными формами ответности являются бухгалтерский баланс и отчет о прибылях и убытках.
Специально организованное наблюдение
Заключается в получении данных, которые в силу тех или иных причин не вошли в отчетность или для проверки данных отчетности. Представляет собой сбор данных посредством переписей и единовременных учетов.
Регистровое наблюдение
Основано на ведении статистического регистра, с помощью которого осуществляется непрерывный статистический учет за долговременными процессами, имеющими фиксированное начало, стадию развития и фиксированное окончание.
Виды статистического наблюдения
Статистические наблюдения подразделяются на виды по следующим признакам:
по времени регистрации данных;
по полноте охвата единиц совокупности;
Виды статистического наблюдения по времени регистрации:
Текущее (непрерывное) наблюдение - проводится для изучения текущих явлений и процессов. Регистрация фактов осуществляется по мере их свершения. (регистрация семейных браков и разводов)
Прерывное наблюдение — проводится по мере необходимости, при этом допускаются временные разрывы в регистрации данных:
Периодическое наблюдение — проводится через сравнительно равные интервалы времени (перепись населения).
Единовременное наблюдение — осуществляется без соблюдения строгой периодичности его проведения.
По полноте охвата единиц совокупности различают следующие виды статистического наблюдения:
Сплошное наблюдение — представляет собой сбор и получение информации обо всех единицах изучаемой совокупности. Характеризуется высокими материальными и трудовыми затратами, недостаточной оперативностью информации. Применяется при переписи населения, при сборе данных в форме отчетности, охватывающей крупные и средние предприятия разных форм собственности.
Несплошное наблюдение — основано на принципе случайного отбора единиц изучаемой совокупности, при этом в выборочной совокупности должны быть представлены все типы единиц, имеющихся в совокупности. Имеет ряд преимущств перед сплошным наблюдением: сокращение временных и денежных затрат.
Несплошное наблюдение подразделяется на:
Выборочное наблюдение - основано на случайном отборе единиц, которые подвергаются наблюдению.
Монографическое наблюдение — заключается в обследовании отдельных единиц совокупности, характеризующихся редкими качественными свойствами. Пример монографического наблюдения: характеристика работы отдельных предприятий, для выявления недостатков в работе или тенденций развития.
Метод основного массива — состоит в изучении самых существенных, наиболее крупных единиц совокупности, имеющих по основному признаку наибольший удельный вес в изучаемой совокупности.
Метод моментных наблюдений — заключается в проведении наблюдений через случайные или постоянные интервалы времени с отметками о состоянии исследуемого объекта в тот или иной момент времени.
Способы статистического наблюдения
Способы получения статистической информации:
Непосредственное статистическое наблюдение — наблюдение, при котором сами регистраторы путем непосредственного замера, взвешивания, подсчета устанавливают факт подлежащий регистрации.
Документальное наблюдение — основано на использовании различного рода документов учетного характера.
Включает в себя отчетный способ наблюдения — при котором предприятия представляют статистические отчеты о своей деятельности в строго обязательном порядке.
Опрос - заключается в получении необходимой информации непосредственно от респондента.
Существуют следующие виды опроса:
Экспедиционный — регистраторы получают необходимую информацию от опрашиваемых лиц и сами фиксируют ее в формулярах.
Способ саморегистрации — формуляры заполняются самими респондентами, регистраторы только раздают бланки и объясняют правила их заполнения.
Корреспондентский — сведения в соответствующие органы сообщает штат добровольных корреспондентов.
Анкетный — сбор информации осуществляется в виде анкет, представляющих собой специальные вопросники, удобен в случаях, когда не требуется высокая точность результатов.
Явочный — заключается в предоставлении сведений в соответствующие органы в явочном порядке.
овокупности.
2. Относительные величины: виды и особенности их применения в экономическом анализе (указать формулы и дать примеры).
Относительные величины в статистике представляют собой частное от деления двух статистических величин и характеризуют количественное соотношение между ними.
При расчете относительных величин следует иметь в виду, что в числителе всегда находится показатель, отражающий то явление, которое изучается, т.е. сравниваемый показатель, а в знаменателе — показатель, с которым производится сравнение, принимаемый за основание, или базу сравнения. База сравнения выступает в качестве своеобразного измерителя. В зависимости от того, какое числовое значение имеет база сравнения (основание), результат отношения может быть выражен либо в форме числа (коэффициента) или процента, либо в форме промилле или децимилле. Существуют также именованные относительные величины. Например, показатель фондоотдачи в торговле получают делением объема товарооборота на среднегодовую стоимость основных фондов. Этот коэффициент показывает, сколько рублей товарооборота приходится на каждый рубль основных фондов.
Если значение основания или базы сравнения принимается за единицу (приравнивается к единице), то относительная величина (результат сравнения) является коэффициентом и показывает, во сколько раз изучаемая величина больше основания. Расчет относительных величин в виде коэффициента применяется в том случае, если сравниваемая величина существенно больше той, с которой она сравнивается. Если значение основания или базу сравнения принять за 100%, результат вычисления относительной величины будет выражаться также в процентах.
В тех случаях, когда базу сравнения принимают за 1000 (например, при исчислении демографических коэффициентов), результат сравнения выражается в промилле (%о). Относительные величины могут быть выражены и в децимилле, если основание отношения равно 10000 (%оо).
Форма выражения относительных величин зависит от количественного соотношения сравниваемых величин, а также от смыслового содержания полученного результата сравнения. В тех случаях, когда сравниваемый показатель больше основания, относительная величина может быть выражена или коэффициентом, или в процентах. Когда сравниваемый показатель меньше основания, относительную величину лучше выразить в процентах; если же сравнительно малые по числовому значению величины сопоставляются с большими, относительные величины выражаются в промилле. Так, в промилле рассчитываются коэффициенты рождаемости, смертности, естественного и механического прироста населения.
В каждом отдельном случае следует выбирать ту форму выражения относительных величин, которая более наглядна и легче воспринимается. Например, лучше сказать, что объем товарооборота магазина за анализируемый период вырос почти в 2 раза, чем сказать, что объем товарооборота составил 199,5%.
Расчет относительных величин может быть правильным лишь при условии, что показатели, которые сравниваются, являются сопоставимыми. Причины, вызывающие несопоставимость показателей, неодинаковы, например различия в методологии сбора, обработки статистической информации, в длительности периодов времени, за которые исчислены сравниваемые показатели, и др. Во всех этих случаях расчет относительных величин можно выполнять только после приведения изучаемых показателей к сопоставимому виду.
По своему познавательному значению относительные величины подразделяются на следующие виды:, структура, динамика, сравнение, координация, интенсивность.
Относительные величины структуры характеризуют состав изучаемых совокупностей. Исчисляются они как отношение абсолютной величины каждого из элементов совокупности к абсолютной величине всей совокупности, т.е. как отношение части к целому, и представляют собой удельный вес части в целом. Как правило, относительные величины структуры выражаются в процентах (база сравнения принимается за 100). Показатели структуры могут быть выражены также в долях (база сравнения принимается за 1).
Сравнивая структуру одной и той же совокупности за разные периоды времени, можно проследить структурные изменения, происшедшие во времени.
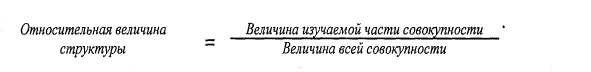
Пример. Из общей численности населения России, равной на конец 1985 г. 143,8 млн. человек, 104,1 млн. составляли городские жители, 39,7 млн. — сельские. Рассчитав относительные величины структуры, можно определить удельные веса (или доли городских и сельских жителей) в общей численности населения страны, т.е. структуру населения по месту жительства:
городское — (104,1:143,8) • 100 % = 72,4 %;
сельское — (39,7 :148,7) • 100 % = 27,6 %.
Спустя б лет численность населения страны составила 148,7 млн. человек, в том числе:
городских жителей — 109,7 млн., сельских — 39,0 млн. человек. Исходя из этих данных исчисляются показатели структуры населения:
городское — (109,7 :148,7) • 100 % = 73,8 %;
сельское — (39,0:148,7) • 100 % = 26,2 %.
Сравнив состав населения страны в 1985 г. и в 1991 г., можно сделать вывод о том, что происходит увеличение удельного веса городских жителей.
Относительные величины структуры широко используются в анализе коммерческой деятельности торговли и сферы услуг. Они дают возможность изучить состав товарооборота по ассортименту, состав работников предприятия по различным признакам (полу, возрасту, стажу работы), состав издержек обращения и т.д.
Относительные величины динамики характеризуют изменение изучаемого явления во времени, выявляют направление развития, измеряют интенсивность развития. Расчет относительных величин выполняется в виде темпов роста и других показателей динамики.
Пример. Реализация хлопчатобумажных тканей секцией универмага составила в январе 3956 тыс. руб., в феврале — 4200 тыс. руб., в марте — 4700 тыс. руб.
Темпы роста:
базисные (база — уровень реализации в январе)
Кф/я = 4200: 3950 • 100% = 106,3 %;
Км/я= 4700: 3950 • 100 % = 118,9 %; цепные
Кф/я=4200: 3950-100% = 106,3%;
Км/ф= 4700: 4200 • 100 % = 111,9 %.
Относительные величины сравнения характеризуют количественное соотношение одноименных показателей, относящихся к различным объектам статистического наблюдения.
Пример. По данным Всесоюзной переписи населения 1989 г., численность населения Москвы составила 8967 тыс., а численность населения Ленинграда (ныне Санкт-Петербурга) — 5020 тыс. человек.
Рассчитаем относительную величину сравнения, приняв за базу сравнения численность жителей Санкт-Петербурга: 8967:5020=1,79. Следовательно, численность населения Москвы в 1,79 раза больше, чем Санкт-Петербурга.
Можно использовать относительные величины сравнения для сопоставления уровня цен на один и тот же товар, реализуемый через государственные магазины и на рынке. В этом случае за базу сравнения, как правило, принимается государственная цена.
Относительные величины координации представляют собой одну из разновидностей показателей сравнения. Они применяются для характеристики соотношения между отдельными частями статистической совокупности и показывают, во сколько раз сравниваемая часть совокупности больше или меньше части, которая принимается за основание или базу сравнения, т.е., по существу, они характеризуют структуру изучаемой совокупности, причем иногда более выразительно, чем относительные величины структуры.
Пример. На начало года численность специалистов с высшим образованием, занятых в ассоциации «Торговый дом», составила 53 человека, а численность специалистов со средним специальным образованием — 106 человек. Приняв за базу сравнения численность специалистов с высшим образованием, рассчитаем относительную величину координации:
106:53=2,0:1,0, т.е. на двух специалистов со средним специальным образованием приходится один специалист с высшим образованием.
Относительные величины интенсивности показывают, насколько широко распространено изучаемое явление в той или иной среде. Они характеризуют соотношение разноименных, но связанных между собой абсолютных величин.
В отличие от других видов относительных величин относительные величины интенсивности всегда выражаются именованными величинами.
Рассчитываются относительные величины интенсивности делением абсолютной величины изучаемого явления на абсолютную величину, характеризующую объем среды, в которой происходит развитие или распространение явления. Относительная величина показывает, сколько единиц одной совокупности приходится на единицу другой совокупности.
Примером относительных величин интенсивности может служить показатель, характеризующий число магазинов на 10000 человек населения. Он получается делением числа магазинов в регионе на численность населения региона и умножением на 10000.
|
|
|
|
|
|
3.Средняя арифметическая : простая и взвешенная, особенности их применения (указать формулы и дать примеры).
4.Свойства средней арифметической величины.
Понятие средней арифметической
Средняя арифметическая - такое среднее значение признака, при вычислении которого общий объем признака в совокупности сохраняется неизменным. Для того чтобы вычислить среднюю арифметическую, необходимо сумму всех значений признаков разделить на их число.
Она применяется в тех случаях, когда объем варьирующего признака для всей совокупности является суммой значений признаков отдельных ее единиц. Примером средней арифметической может служить общий фонд заработной платы — это сумма заработных плат всех работников.
Средняя арифметическая может быть вычислена по формуле:
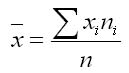
где n — численность совокупности.
Смотрите видео по нахождению средней арифметической величины
Виды средней арифметической величины
Средняя арифметическая величина используется в форме простой средней и взвешенной средней. Средняя арифметическая простая равна простой сумме отдельно взятых значений осредняемого признака, разделенная на общее число этих значений. В различных контрольных по статистике она используется тогда, когда имеются несгруппированные индивидуальные значения признака, и может быть вычислена по формуле:
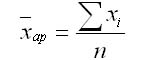
где n — общая численность совокупности значений х.
|
 Скачать 1.31 Mb.
Скачать 1.31 Mb.