Электрохимия. Вопросы коллоквиума к разделу Электрохимия Основные положения теории электролитической диссоциации
 Скачать 6.64 Mb. Скачать 6.64 Mb.
|
|
Вопросы коллоквиума к разделу «Электрохимия» В растворах электролитов присутствует в-ва, способные к электролитической диссоциации-растворы электролитов обладают электропроводностью. Электрохимический процесс является разновидностью гетерогенного процесса, так как он протекает на границе двух фаз: металл- раствор электролита. Электролитическая диссоциация- способность диссоциировать на ионы под влиянием растворителя. Свойства растворов электролитов отличаются от свойств разбавленных растворов. изотонический коэффициент для описания свойств растворов электролитов. Теория электролитической диссоциации связана с введением α-степень диссоциации( делит вещества на сильные и слабые электролиты) Электролиты — это химические соединения, которые в растворе (полностью или частично) диссоциируют на ионы. Различают сильные и слабые электролиты. Сильные электролиты диссоциируют в растворе на ионы практически полностью. Примерами сильных электролитов в водных растворах могут служить некоторые неорганические основания (КОН) и кислоты (НС1), а также большинство неорганических и органических солей. Слабые электролиты диссоциируют в растворе только частично. К слабым электролитам в водных растворах относятся почти все органические кислоты и основания (например, уксусная кислота , пиридин) и некоторые неорганические соединения. Развитие теоретических представлений о строении растворов началось с теории электролитической диссоциации Аррениуса. Эта теория, сформулированная в 1887 г., включает следующие основные положения. При растворении молекулы неорганических и органических кислот, оснований и солей спонтанно диссоциируют на ионы, например: 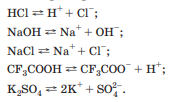 Ионы представляют собой заряженные частицы, которые состоят или из отдельных атомов, или из группы атомов. Предполагалось, что ионы в растворе ведут себя подобно молекулам идеального газа, т. е. не взаимодействуют друг с другом. Физические причины, которые приводят к диссоциации электролитов, в теории Аррениуса не рассматривались. Не обсуждался также и вопрос о том, почему заряженные частицы, на которые должны были бы распространяться законы электростатики, не взаимодействуют друг с другом в растворах. Диссоциация молекул на ионы является неполной, т. е. не все молекулы электролита, а лишь некоторая их доля α, названная степенью диссоциации, распадается на ионы; доля молекул, равная (1 – α), остается недиссоциированной. Таким образом, если при диссоциации одной молекулы электролита образуется ν ионов, то концентрация ионов в растворе оказывается равной ναс, а концентрация недиссоциированных молекул — (1 – α) с. Следовательно, общая молярная концентрация частиц в растворе составит (1 – α)c + ναc=c [l + α(ν – 1)]. Выражение [1 + α(ν – 1)] показывает, во сколько раз увеличивается общая молярная концентрация частиц в растворе за счет диссоциации электролита, т. е. эквивалентно по своему физическому смыслу изотоническому коэффициенту Вант-Гоффа i. Поэтому по теории Аррениуса i =l+ α(ν – 1). (1.2.1) Поскольку ν > 1, а α > 0, то i > 1, и уравнение (1.2.1) позволяет дать разумное объяснение экспериментальным данным по осмотическому давлению, по изменению давления пара над растворами, а также по снижению температуры замерзания и по повышению температуры кипения растворов электролитов по сравнению с чистыми растворителями. К процессу электролитической диссоциации применим закон действующих масс. Так, если в результате диссоциации молекулы электролита МА получается один катион М+ и один анион A– (МА =M+ + А– ), то концентрации молекул и ионов равны соответственно: [МА] = с (1 – α); [M+ ] = [A– ] = αc, и для константы электролитической диссоциации K по теории Аррениуса получаем следующее выражение: 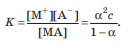 (1.2.2) (1.2.2) Поскольку обратная величина молярной концентрации V = 1/c называется разведением, то уравнение (1.2.2) или аналогичное уравнение с заменой c = 1/V называется законом разведения Оствальда. По теории Аррениуса константа K является постоянной для данного электролита. Поэтому по уравнению (1.2.2) можно рассчитать степень диссоциации в зависимости от концентрации электролита. Решая квадратное уравнение и учитывая, что α > 0, получаем: 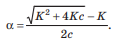 (1.2.3) (1.2.3) Как следует из уравнения (1.2.3), при условии К>>4с α→1, т. е. электролит становится полностью диссоциированным . С другой стороны, при малых константах диссоциации и при не очень низких концентрациях, когда К>>4с , 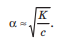 (1.2.4) (1.2.4) Соотношения (1.2.2)–(1.2.4) применимы только для растворов симметричных бинарных электролитов (т. е. если одна молекула электролита дает один катион и один анион). Если же электролит имеет несимметричный валентный тип или имеется смесь электролитов, то математические соотношения, описывающие закон действующих масс согласно теории Аррениуса, и вытекающие из них следствия усложняются. Теория Аррениуса позволила трактовать любые явления, связанные с ионными равновесиями, и легла, таким образом, в основу качественного и количественного анализа . Сильные и слабые электролиты. Средний коэффициент активности. Правило ионной силы. Различают сильные и слабые электролиты. Сильные электролиты диссоциируют в растворе на ионы практически полностью. Примерами сильных электролитов в водных растворах могут служить некоторые неорганические основания (КОН) и кислоты (НС1, НNO3), а также большинство неорганических и органических солей. Слабые электролиты диссоциируют в растворе только частично. Доля продиссоциировавших молекул из числа первоначально взятых называется степенью диссоциации. К слабым электролитам в водных растворах относятся почти все органические кислоты и основания (например, уксусная кислота , пиридин) и некоторые неорганические соединения. В настоящее время в связи с развитием исследований неводных растворов доказано (Измайлов и др.), что сильные и слабые электролиты являются двумя различными состояниями химических соединений (электролитов) в зависимости от природы растворителя. В одном растворителе данный электролит может быть сильным электролитом, в другом — слабым. Рассмотрим сильный электролит 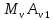 ; он полностью диссоциирует на ионы: ; он полностью диссоциирует на ионы: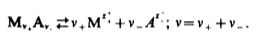 (1) (1)В связи с требованием электро нейтральности раствора химический потенциал рассматриваемого электролита (в целом) μ2 связан с химическими потенциалами ионов μ- и μ+ соотношением: μ2= 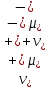 (2) (2)Химические потенциалы составляющих электролита связаны с их активностями следующими уравнениями: 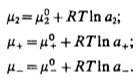 (3) (3)Подставляя эти уравнения в соотношение (2), получаем: Выберем стандартное состояние μ2 таким образом, чтобы между стандартными химическими потенциалами и было справедливо соотношение,по форме аналогичное уравнению (2): 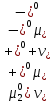 (5) (5)С учетом уравнения (5) соотношение (4) после сокращения одинаковых слагаемых и одинаковых множителей (RT) приводится к виду В связи с тем, что активности отдельных ионов не определяются из опыта, введем понятие средняя активность ионов электролита как среднее геометрическое из активностей катиона и аниона электролита: 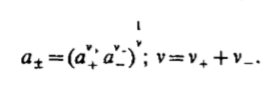 (7) (7)Среднюю активность ионов электролита можно определить из опыта. Из уравнений (6) и (7) получаем 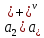 (8) (8)Активности катиона и аниона можно выразить соотношениями: 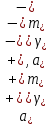 (9) (9)где у+ и у_ — коэффициенты активности катиона и аниона; 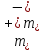 — модальность катиона и аниона в растворе электролита: — модальность катиона и аниона в растворе электролита: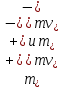 (10) (10)Подставляя значения а+ и а_ из (9) в (7), получаем 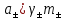 (11) (11)где у± — средний коэффициент активности электролита: 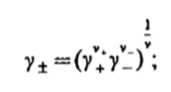 (12) (12)Средний коэффициент активности электролита у± представляет собой среднее геометрическое из коэффициентов активности катиона и аниона, а средняя концентрация ионов электролита т ± — среднее геометрическое из концентраций катиона и аниона. Подставляя значения т+ и т_ из уравнения (V IIЛ 0) в (VII. 13), получаем m±-mv±, (14) v ± = (v > _ )V. Средний коэффициент активности бинарного 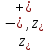 - валентного электролита можно рассчитать по выведенному Дебаем и Хюккелем уравнению - валентного электролита можно рассчитать по выведенному Дебаем и Хюккелем уравнению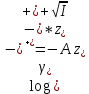 (1) (1)Где γ 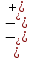 средний коэф. активности средний коэф. активностиI — ионная сила; А = 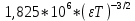 где 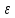 — диэлектрическая проницаемость растворителя. — диэлектрическая проницаемость растворителя. В разбавленном водном растворе при 298 К , 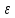 =78,3 и А = 0,509. =78,3 и А = 0,509. Уравнение (1) применимо только к сильно разбавленным электролитам н называется предельным законом Дебая — Хюккеля. При данной ионной силе раствора средний коэффициент активности электролита в предельно разбавленном растворе является величиной постоянной и не зависит от природы других электролитов в растворе. Таким образом, в предельном законе Дебая — Хюккеля получает теоретическое обоснование правило ионной силы. Согласно правилу ионной силы: разбавленных растворах средний коэффициент активности электролита зависит только от ионной силы раствора и не зависит от природы других ионов, находящихся в растворе. Это правило справедливо при концентрации раствора менее 0,01—0,02 моль/кг, но приближенно им можно пользоваться до концентрации ОД — 0,2 моль/кг. Предельный закон Дебая — Хюккеля удовлетворительно описывает также зависимость среднего коэффициента активности электролита от температуры, диэлектрической проницаемости растворителя, заряда ионов и т. п, при предельном разбавлении раствора. Одно из упрощений при выводе уравнения (1) заключалось в том, что вместо реального центрального иона рассматривался точечный заряд. Если учесть размер центрального иона, то получается более точное уравнение (выведенное тоже Дебаем и Хюккелем): 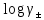 = =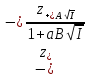 (2) (2)где В — теоретический коэффициент, равный для водных растворов при 298 К , 0,33* 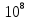 ; а — средний эффективный диаметр ионов, находят из опыта. ; а — средний эффективный диаметр ионов, находят из опыта. Уравнение (2) удовлетворительно согласуется со средними коэффициентами активности электролита, когда коэффициент активности уменьшается с увеличением концентрации электролита. Но уравнение (2) не может объяснить увеличения среднего коэффициента активности с ростом концентрации электролита. Под ионной силой понимается: 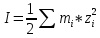 Где 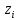 - заряд кк катиона, так и аниона - заряд кк катиона, так и аниона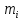 - моляльная концентрация - моляльная концентрациязарядный электролит z=1 NaCl= 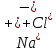 I=m I=mУравнение (1) теоретически обосновывает закон ионной силы: при одинаковой ионной силе и одинаковой силе электролита с точки зрения зарядности 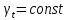 Коэффициент активности ∞ разбавленных растворов принимается =1, следовательно I -> 0 С ростом концентрации коэффициент активности уменьшается сначала, а при высоких концентрациях- растет и принимает значения больше 1. Это обусловлено увеличением сил отталкивания одноименных ионов. Степень и константа диссоциации слабых электролитов. Закон разведения Оствальда. Теория электролитической диссоциации связана с введением α-степень диссоциации( делит вещества на сильные и слабые электролиты) Для слабых электролитов известен закон разбавления Оствальда: АВ ↔ 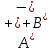 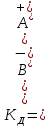 Константа равновесия процесса диссоциации слабого электролита называется константой диссоциации. Величина K зависит от природы электролита и растворителя, а также от температуры. Она характеризует способность данного электролита распадаться на ионы в растворе. Чем больше K, тем полнее диссоциирует электролит в растворе. Концентрация используется равновесная. Степень диссоциации электролита определяют по уравнению a = 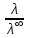 , , где l – молярная электропроводность раствора, l¥ – молярная электропроводность электролита при бесконечном разведении. Молярная электрическая проводимость l связана с удельной электрической проводимостью k соотношением l = 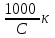 . . Величину l¥ рассчитывают по справочным данным по уравнению l¥ = l¥+ + l¥– , где l¥+ и l¥– – подвижности ионов при предельном разбавлении. Если α- степень диссоциации, С-концентрация раствора электролита, то 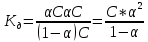 -закон разбавления Оствальда -закон разбавления ОствальдаС увеличением концентрации слабого электролита уменьшается степень диссоциации. Теория растворов сильных электролитов. Предельный закон Дебая–Хюккеля. Сильные электролиты имеют высокую степень диссоциации, т.е полностью диссоциируют на ионы, значит, равновесие смещено вправо В 1923г. Дебай и Гюккель ввели ряд положений: Ионы, присутствующие в растворе взаимодействуют друг с другом электростатически. Р-ль влияет на взаимодействие, это учитывается диэлектрической постоянной р-ля. Центральный ион взаимодействует с окружающими ионами, которые представляют собой ионную атмосферу. Центральный ион имеет св-ва точечного заряда (размеры очень малы) Любой ион в составе раствора электролита может считаться центральным ионом, т.е. центральный ион и ионная атмосфера могут меняться относительно друг друга в зависимости как меняется система. Электростатическое взаимодействие ионов объединяет различия свойств сильных электролитов от идеальных растворов. Для оценки этого влияния вводится характеристика: γ 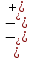 средний коэф. активности средний коэф. активности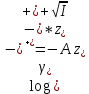 (1) (1)Где А- постоянная( зависит от Т и природы растворителя) 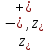 - заряд аниона и катиона - заряд аниона и катионаI- ионная сила электролита Уравнение (1) «Дебая-Хюккеля» справедливо для разбавленных растворов ; в растворах электролитов высокой концентрации соблюдается лишь приближенно, и называется предельным законом Дебая — Хюккеля. Под ионной силой понимается: 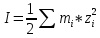 Где 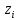 - заряд кк катиона, так и аниона - заряд кк катиона, так и аниона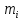 - моляльная концентрация - моляльная концентрациязарядный электролит z=1 NaCl= 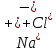 I=m I=mУравнение (1) теоретически обосновывает закон ионной силы: при одинаковой ионной силе и одинаковой силе электролита с точки зрения зарядности  |
